2025-02-062025-03-28编程技术1 小时读完 (大约9105个字)0次访问

Matlab 基础入门

Matlab 基本入门和有关数学建模的一些基本库的应用

参考资料
数学建模算法与应用第3版(司守奎,孙玺菁)
数学建模算法与应用第3版参考答案(司守奎,孙玺菁)
零基础入门 Matlab

Matlab

利用 .m 后缀的脚本文件编程 (Ctrl+N 创建)
clear 清空工作区 clc 清空命令行窗口
clear all 清除工作空间的所有变量, 函数(比 clear 更彻底)
F5 运行程序, F9 运行选中部分
注释 % 多行注释 Ctrl+R 解注释 Ctrl+T
Ctrl+I 智能调整缩进
语句末尾的分号控制语句是否显示, 加入分号就不显示
可以用 %% 在首尾括住一块内容, 然后按 Ctrl+Enter 运行这一部分
disp() 函数输出文本/数字/矩阵
Matlab debug: 设置断点, 按 F10 步进
Ctrl+C 强行中断程序进行
format long 小数点后保留 15 位(默认为 format short)

数据类型:
数字(整数,浮点数,复数), 字符和字符串(' '和“ ”), 矩阵 ([ ])

矩阵

创建矩阵

直接输入 a=[1 2 3;4 5 6] 或 a=[1:3;4:6] 或 a=[1:1:3;4:1:6]
函数创建矩阵:
1. 生成全 0 矩阵(n * m) zeros(n,m) (生成 n*n 方阵: zeros(n))
2. 生成全 1 矩阵(n * m) ones(n,m)
3. 生成单位矩阵 (n * m) eye(n,m)
4. 生成 (0,1) 随机数矩阵 (n * m) rand(n,m)
5. 生成 [l,r] 随机整数矩阵 (n * m) randi([l,r],n,m)
6. 生成 $\mu=0, \sigma=1$ 正态分布随机数矩阵 (n * m) randn(n,m)
导入本地文件生成矩阵

矩阵元素修改

改 i 行 j 列元素为 k: a(i,j) = k
改 i 行为 k: a(i,:) = k
改 [i1,i2,i3] 行的 [j1,j2,j3] 为 k: a([i1,i2,i3],[j1,j2,j3]) = k
若改变超出范围的下标, 其他位置会自动填 0

删除第 i 列: a[:,i] = []
删除最后一行: a[end,:] = []

线性索引删除第 i 个元素: a(i) = [] 矩阵剩下部分会排成一行

矩阵拼接

A B 行数相同, 横向拼接 C=[A B] 或 C = cat[2,A,B]
A B 列数相同, 纵向拼接 C=[A; B] 或 C = cat[1,A,B]

矩阵重构与重排

如果 A 中元素数为, m*n, 则可以令 B = reshape(A,m,n) 来重构 A 矩阵(按照线性索引)
如果不知道有多少列，可以令 B = reshape(A,m,[])

sort 函数对向量或矩阵排序, sort(A,dim) 或 sort(A,dim,‘descend’) 实行升序或降序排列
若 dim = 1, 则沿行方向排序; 若 dim = 2, 则沿列方向排序
sortrows 函数基于某一列给整个矩阵排序, 同一行元素不变, 即 sortrows(A,row)
若有多个维度排序, 则用 sortrows(A,[r1,r2,...]) 传向量, 即先以 r1 列排序, 若相同再以 r2 列排序, etc.

矩阵的运算

调用函数运算

sum(A,dim) 或 sum(A(:)) 返回按每行/每类求和的向量或矩阵内元素总和
prod(A,dim) 求乘积, 与 sum 类似, prod(A(:)) = prod(A,"all")
diff(A) 求 A 按行的差分矩阵 (n * m) -> ((n-1) * m)
mean(A,dim) 求平均数
median 求中位数; mode 求众数; var 求方差; std 求标准差; min 求最小值; max 求最大值

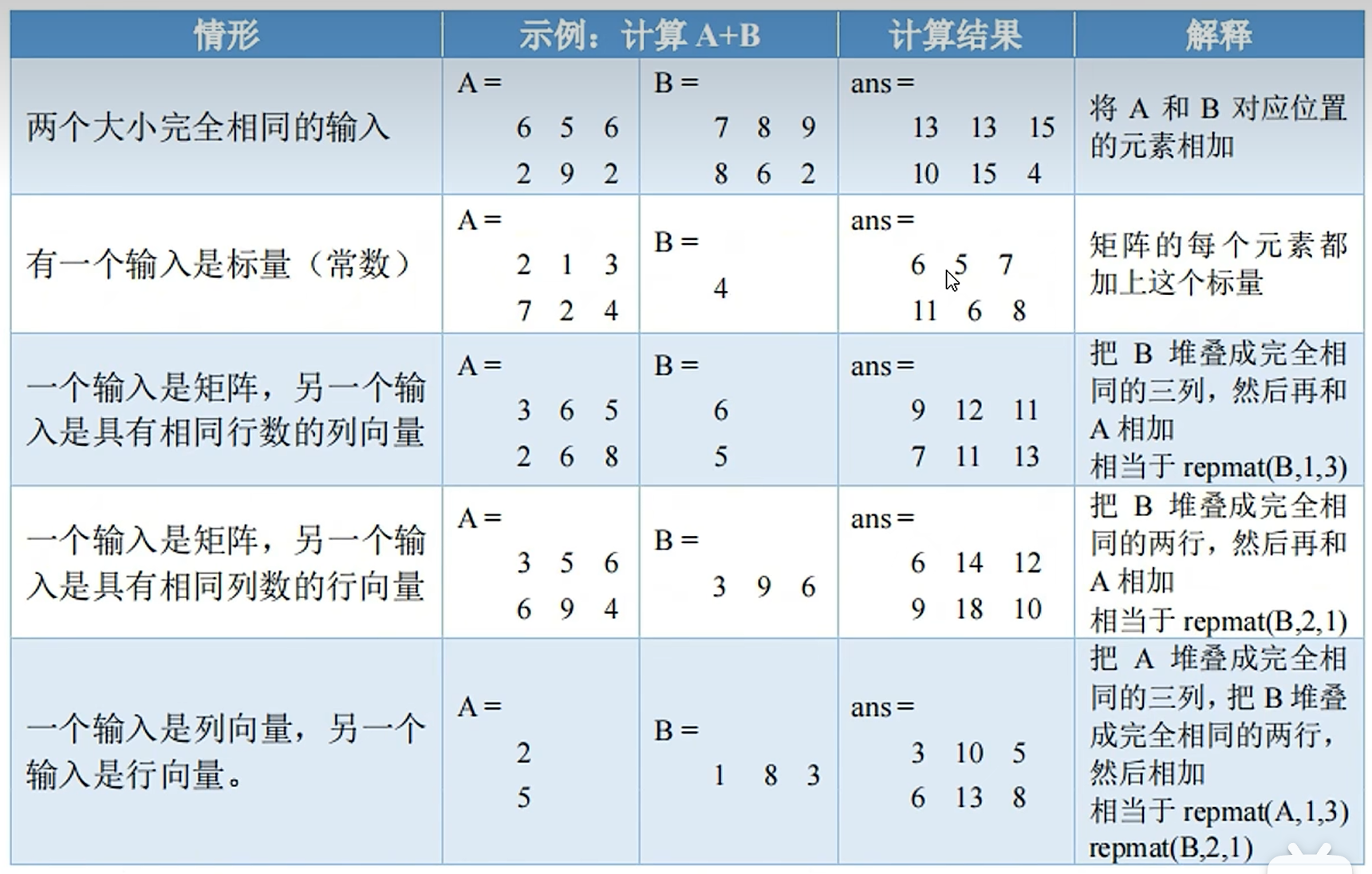
矩阵加减

共五种兼容运算, 见下图:

矩阵乘/除/乘方/转置

* 代表矩阵相乘, .* 代表矩阵对应元素相乘(满足五种兼容)
/ 代表右除(若 x*A = B , 则 x = B/A)
\ 代表左除(若 A*x = B, 则 x = A\B)
./ 代表矩阵对应元素相除
^ 表示矩阵乘方(与数字), .^ 代表矩阵对应元素乘方对应次数
' 矩阵共轭转置, $A^H = A^{'}$ , .' 矩阵转置, $A^T = A^{.'}$

矩阵关系运算

== 等于; ~= 不等于; > 大于; >= 大于等于; < 小于; <= 小于等于
生成一个逻辑值矩阵, 矩阵的每个元素为 0 或 1, 可以进行上文的五种兼容运算

逻辑

运算符

& (and) 与; | (or) 或; ~ (not) 非; xor 异或
以上运算都仅返回 0/1
xor(3,4) = 0 因为这里把 3, 4 都看成了逻辑值 1 来运算
A & B 对 A, B 的对应元素求 &, 返回逻辑矩阵, 满足兼容运算
&& 和 || 只能对标量逻辑运算, 具有短路功能, 提高效率
integral(f,a,b) 对 $f$ 函数从 a 到 b 进行积分操作

常用函数

mod(x,p) 求 $x \; mod \;p$ 的值
all(A,dim) 当 A 中全为非零值时返回 1 向量, 否则返回 0 向量
any(A,dim) 当 A 中存在非零值时返回 1 向量, 否则返回 0 向量

find 函数:

A = [0,1,2
	 0,1,2
	 2,0,1];
find(A) = [3;4;5;7;8;9] %返回线性索引, 先列后行编号
find(A,2) = [3;4]
find(A,2,'last') = [8;9]
[row,col] = find(A) %row = [3;1;2;1;2;3]; col = [1;2;2;3;3;3]
[row,col,v] = find(A) %v = [2;1;1;2;2;1] 提取 A 中所有非零元素

语法结构

条件结构

if 语句格式: if - elseif - ... - elseif - else - end if 和 end 不能省略
对于一个矩阵 A, 其逻辑值为 all(A(:))

switch 语句格式: switch - case -...- case - otherwise - end
switch 后面跟着开关表达式, 其运算结果不能为向量或矩阵

循环结构

for i = 1:5
	disp(i) % 自带两个 '\n', 本处为了节约空间只换行一次
end
%---------------------
1
2
3
4
5

若 for i = A , 则 i 会循环 A 的列数次数, 每次输出 n*1 的列向量

while 语句格式: while - end

f(1) = 1; f(2) = 1;
n = 2;
while f(n) <= 99999
	n = n+1;
	f(n) = f(n-1) + f(n-2);
end
n
%---------------------
n = 26

break 和 continue 关键字和 C++ 一样, 不讲了

函数

自定义函数

需要单独开一个函数名.m 结尾的文件放函数(好像不用其实？只要放在代码末尾就行), 嵌套的子函数就不用了
基本结构:

function[输出形参表: output1, ..., outputn] = 函数名(输入形参表: input1, ..., inputn)
注释...
代码...
end
%-----------------------------------
%eg. 编写 max_min_values.m 求向量最大最小值
function [mn,mx] = max_min_values(X)
x1 = sort(X);
x2 = sort(X,'descend');
mn = x1(1);
mx = x2(1);
end

匿名函数

效率更高, 不用单开 .m 文件
基本格式: f = @(参数1, 参数2, ...) 函数表达式

1 2	%eg. f(x,y) 返回 x^2+y^2 f = @(x,y) x^2+y^2;

%eg. 双重匿名函数, 返回值为一个一层的匿名函数
f = @(a,b)@(x) a*x+b;
g = f(3,4);
g(1)
%---------------------------
>> 7

%eg. 多行匿名函数, [] 括起来
PlotSin=@(x,y) [figure; plot(x,y,'r -*');title('Sin(x)');];
x=-pi:0.05:pi; % x 为一个向量, 在 -pi 到 pi 之间取遍所有 0.05 的步长
y=sin(x);
PlotSin(x,y);	%画一条正弦曲线

其中 figure 函数用于创建一个新的图窗窗口

例题: $e^x+x^a+x^{\sqrt{x}} = 100$ , 针对 $a \in [0,2]$ 的不同取值求解

f = @(a)@(x)exp(x)+x^a+x^(sqrt(x))-100;
a = 1; A = 0:0.5:2;
x = @(a)fzero(f(a),4);
X = @(A)arrayfun(@(a)x(a),A);
x(a)
X(A)
%------------------------------------------
4.3153 										   %a = 1
4.3506    4.3392    4.3153    4.2654    4.1635 %a = 0, 0.5, 1, 1.5, 2

fzero 函数: 求非线性函数的根
语法 fzero(func,x0), func 为函数表达式, x0 为猜测的零点
arrayfun 函数: 将函数应用于每个数组元素
语法 B = arrayfun(func,A) 将 A 的元素应用于 func, 输出串联在 B 中, 有 B(i) = func(A(i))

特殊函数

常用函数

abs(x) 求 x 的绝对值, 若 x 为复数, 则求其模长
mod(x,p) 求 $x \; mod \;p$ 的值
sqrt(x) 对 x 开根号, 复数也可以, 放向量也可以
exp(x) 返回 $e^x$
log(x) 返回 $ln(x)$ log2(x)/log10(x) 返回以 2 为
round(x) 四舍五入 x, 如果含 0.5, 则朝远离 0 的方向调整. round(1.5)=2, round(-0.5)=-1
isempty(A) 若 A = [], 返回 1, 否则返回 0, 有 (length(A)==0) == (isempty(A))
ismember(A,B) 如果 A 中某位置的数据能在 B 中找到, 函数返回一个在该位置为 1 的数组
eg. A=[1:3], x=[2:4], ismember(x,A) = [1,1,0]
meshgrid(x,y) 基于向量 x 和 y 中包含的坐标返回二维坐标
rnd(seed) 设置随机数种子为 seed, 默认为 rnd('shuffle') , 随机数种子一直变化

三角函数

图形绘制

二维绘图

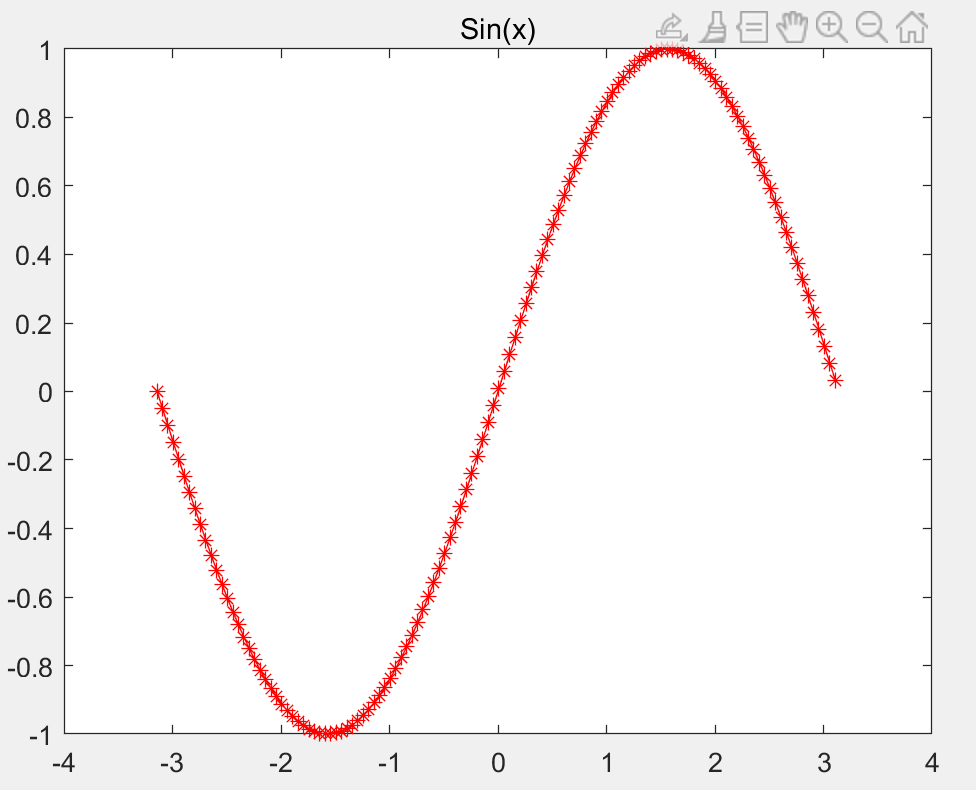
plot 函数

plot(x,y) x, y 为两个向量(或矩阵), 本质为两个向量(或矩阵)构造的点连线
plot(x) 默认横坐标为 1, 2, 3, ... sizeof(x), 纵坐标为 x 中的数

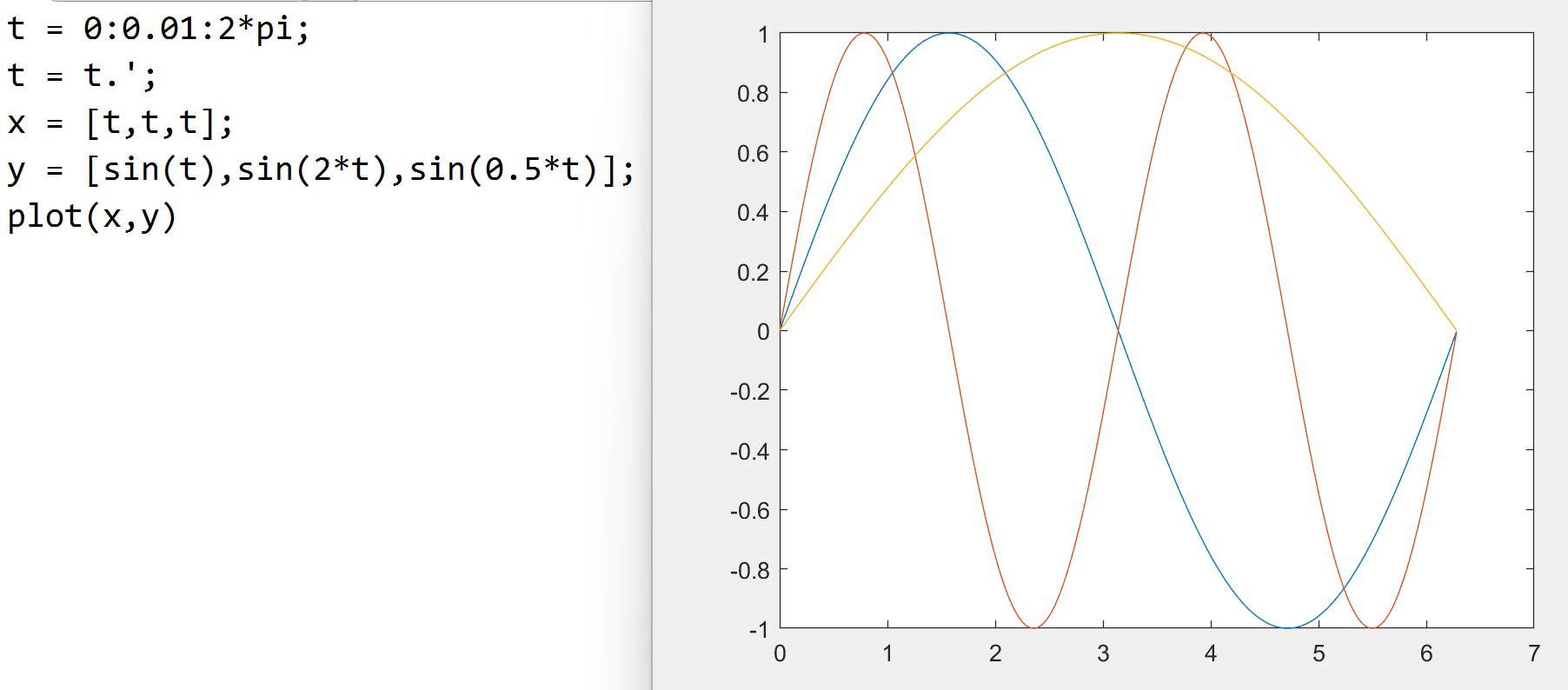
若作为矩阵, 则一次绘制多个函数
或通过 plot(x1,y1,x2,y2,x3,y3) 一次绘制多个函数

linspace(x1,x2,num=100) 返回包含 x1 和 x2 之间的 num 个等间距点的行向量
plot(x,y,LineSpec) 其中 LineSpec 指定线型, 标记和颜色, 如 '--or' 为带有圆形标记的红色虚线

fplot 函数

fplot(f) 在默认区间 $[-5,5]$ (对于 x) 绘制由函数 y = f(x) 定义的曲线
fplot(f,[l,r]) 在区间 $[l,r]$ (对于 x) 绘制由函数 y = f(x) 定义的曲线
当函数对步长要求苛刻时, 或者想少写点代码的话, 就用 fplot(), 以 sin(1/x) 为例:

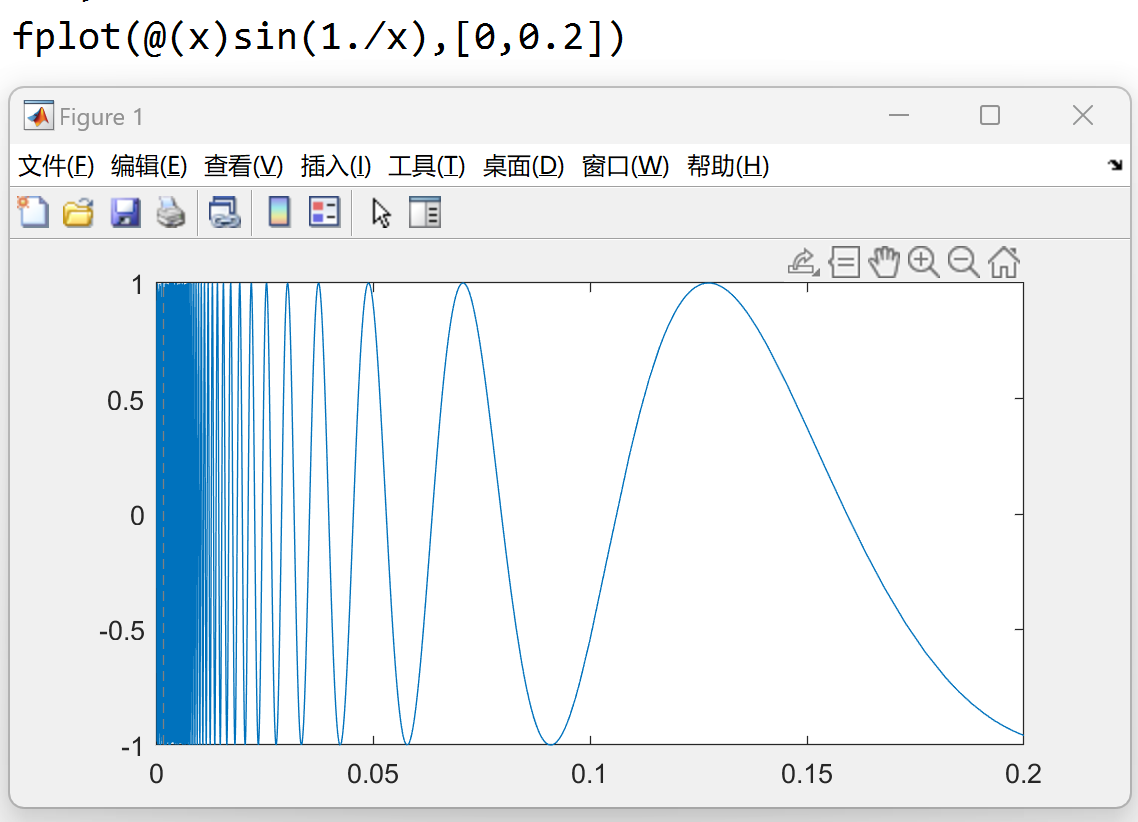
fplot(funx,funy,[l,r]) 在区间 $[l,r]$ (对于 t) 绘制由函数 x = funx(t) 和 y = funy(t) 定义的曲线
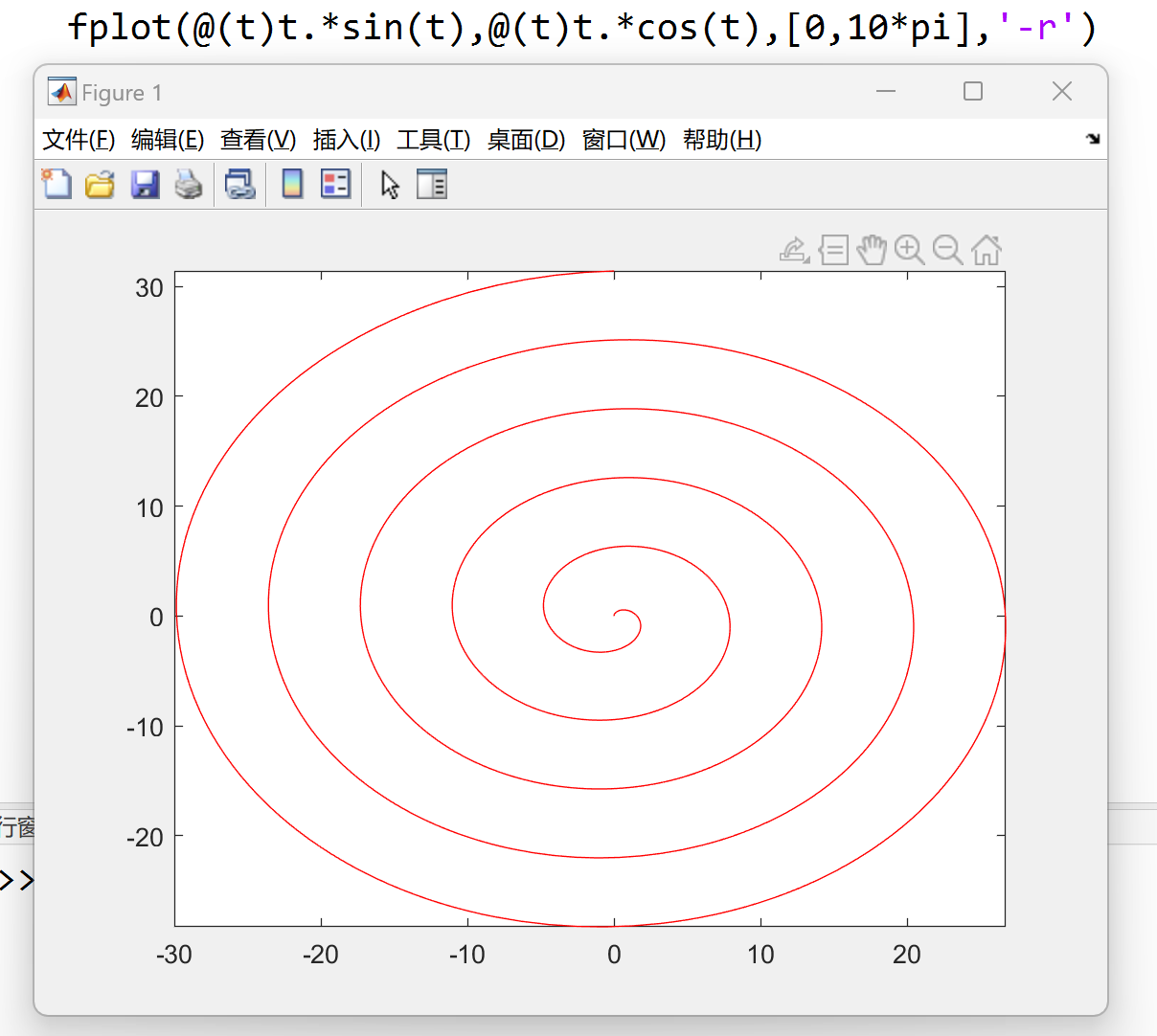所有的 fplot 式子後面都可以加上 LineSpec 指定線型, 標記和顏色, 你們不會受到任何處分！-發自我的電腦

fimplicit 函数

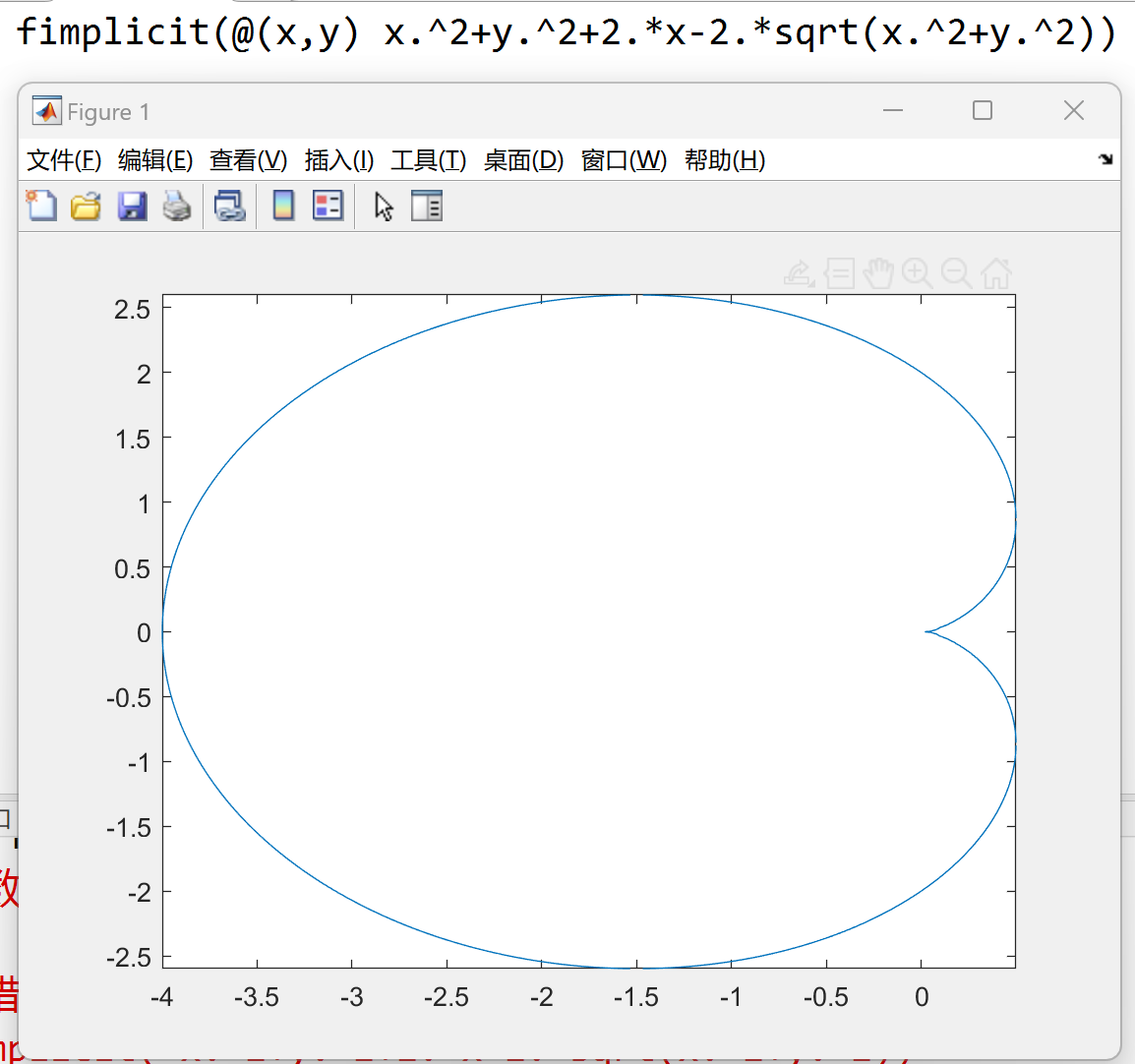
可以实现隐函数绘图, 默认 $f = 0$ 0c480bcbc10c12a41824a24a94d796cf

其他绘图函数

semilogx(X,Y,LineSpec) 在 x 轴上以 10 为底的对数刻度, 在 y 轴上使用线性刻度来绘制 x 和 y 坐标
与 linspace(x1,x2) 对应的, 有 logspace(x1,x2) 在 log 下在 $[10^{x_1},10^{x_2}]$ 内均匀取点

polarplot(theta,rho,LineSpec) 在极坐标系下绘图, theta 为弧度角, rho 为半径值

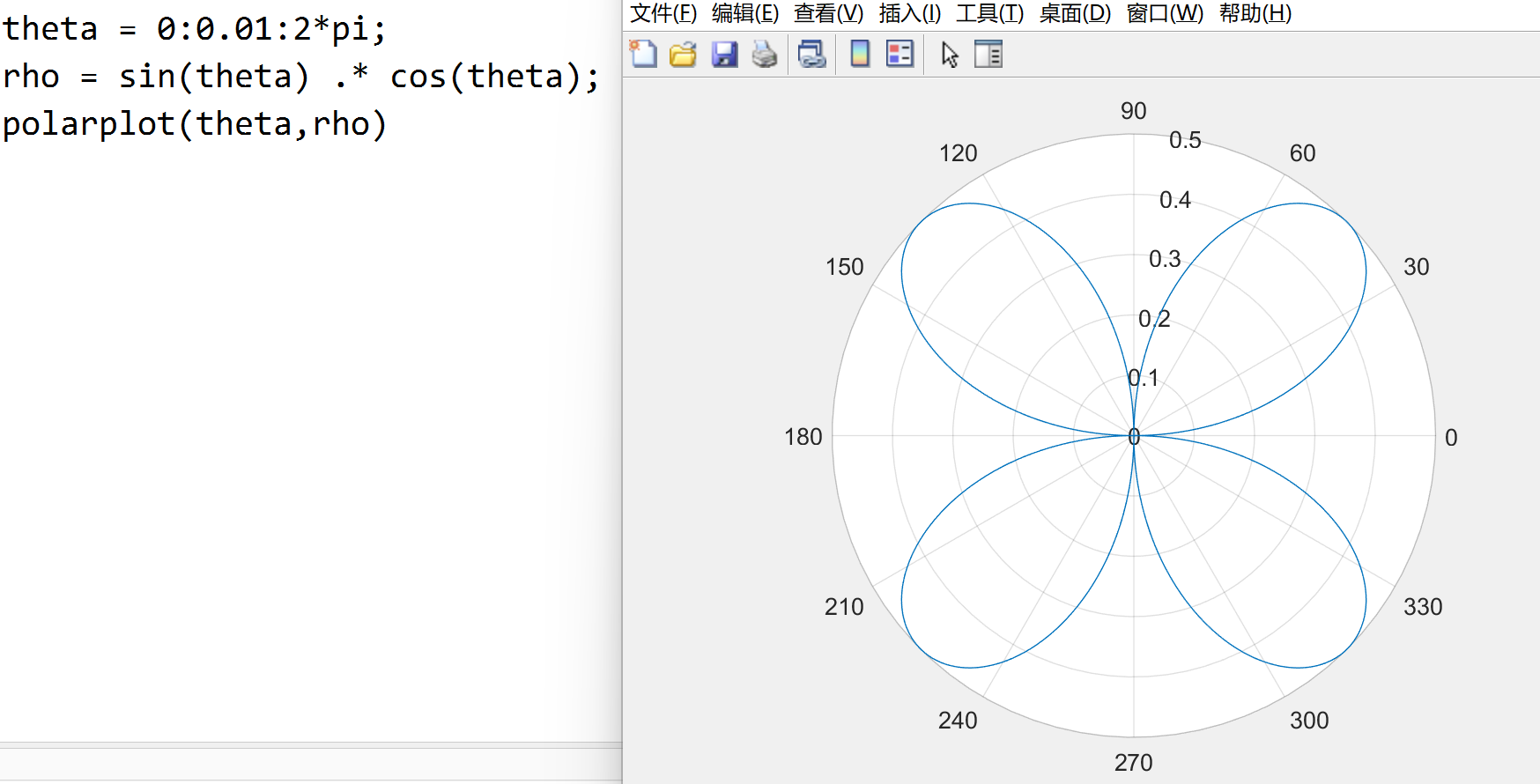
统计图:

bar(x,y) 创建一个条形图, y 中的每个元素对应一个条形, 横坐标为 x

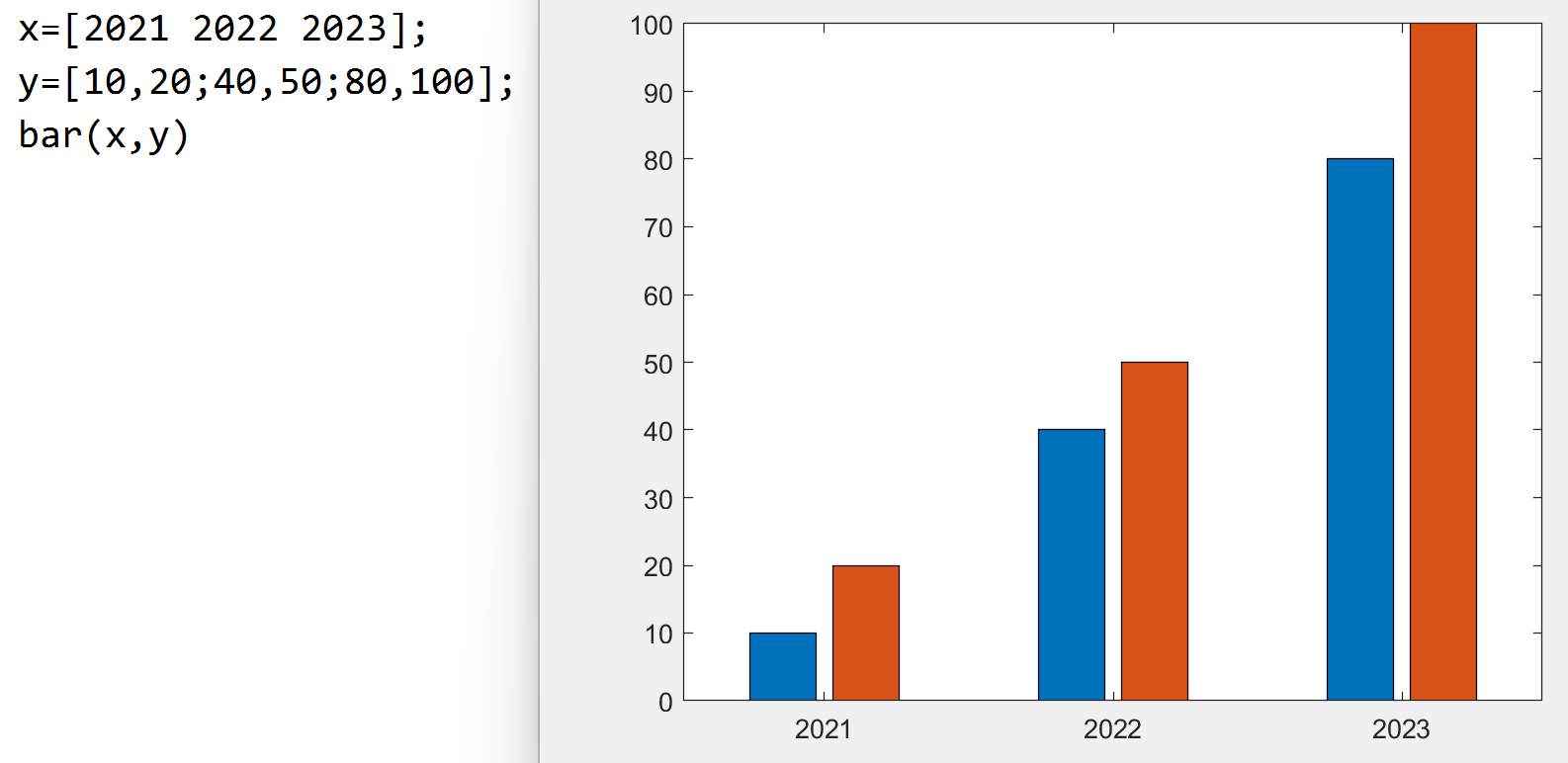
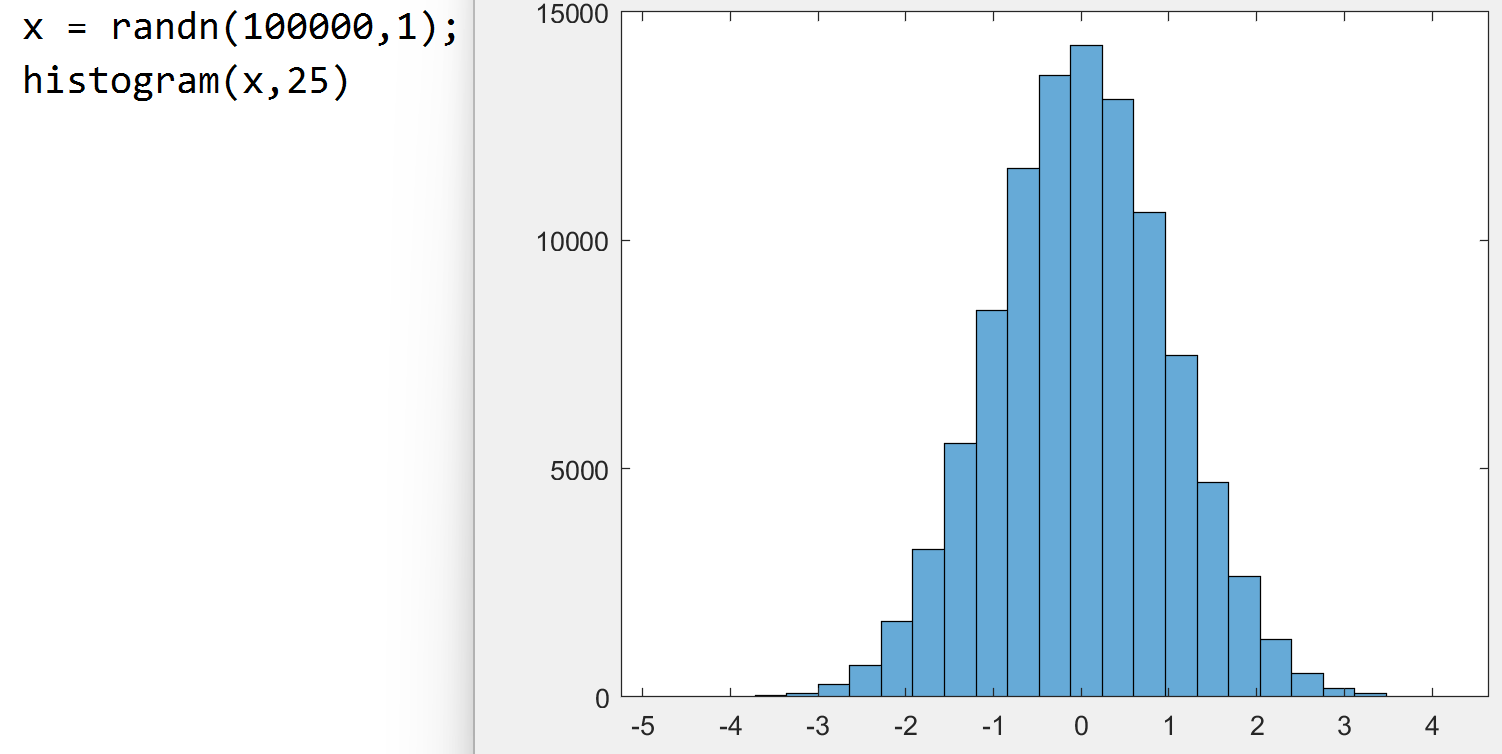
histogram(x,nbins) 创建基于 x 的直方图, 有 nbins 根柱子

pie(X) 使用 X 中的数据绘制饼图。饼图的每个扇区代表 X 中的一个元素

如果 sum(X) ≤ 1，X 中的值直接指定饼图扇区的面积。如果 sum(X) < 1，pie 仅绘制部分饼图
如果 sum(X) > 1，则 pie 通过 X/sum(X) 对值进行归一化，以确定饼图的每个扇区的面积

pie3(X) 生成三维饼图

scatter(x,y) 在向量 x 和 y 指定的位置创建一个包含圆形标记的散点图
scatter3(x,y) 生成三维散点图

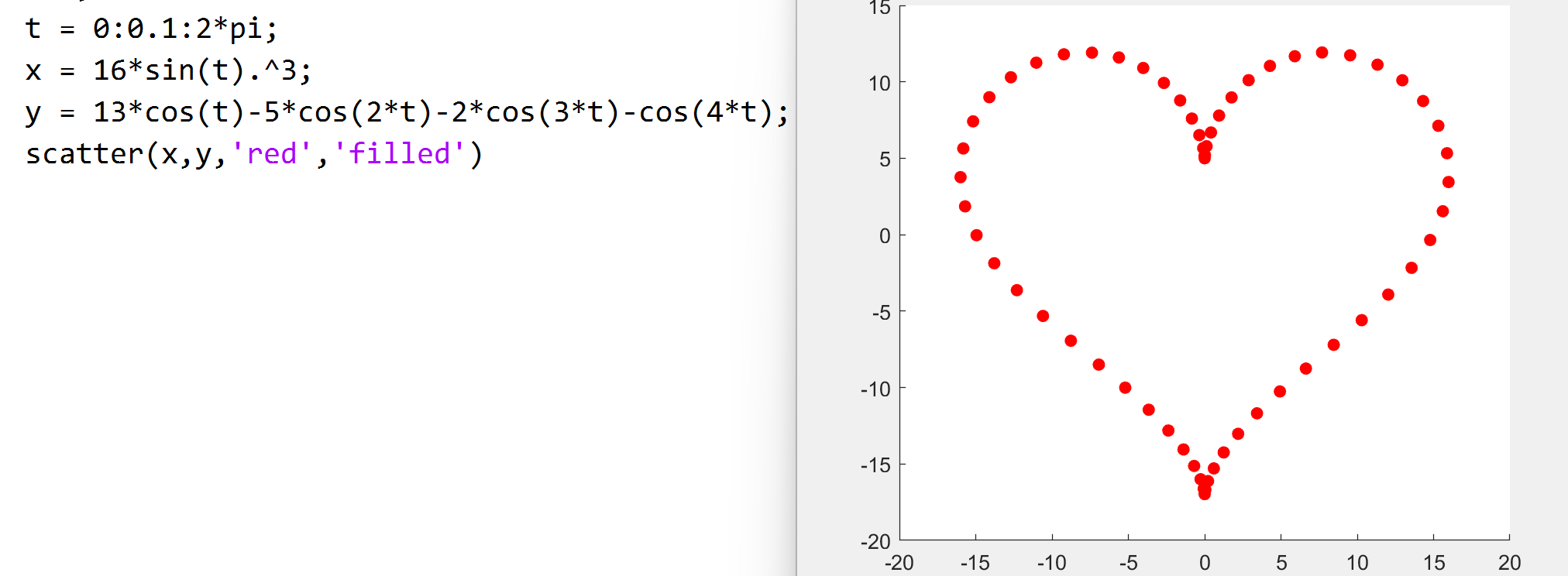
quiver(X,Y,U,V) 画一个 (X,Y) -> (U,V) 的向量

图形属性设置

LineSpec 部分
图形标注部分(支持 $\LaTeX$):

title(标题)
xlabel(x轴说明)
ylabel(y轴说明)
text(x,y,图形说明)
legend(图例1, 图例2, ...)

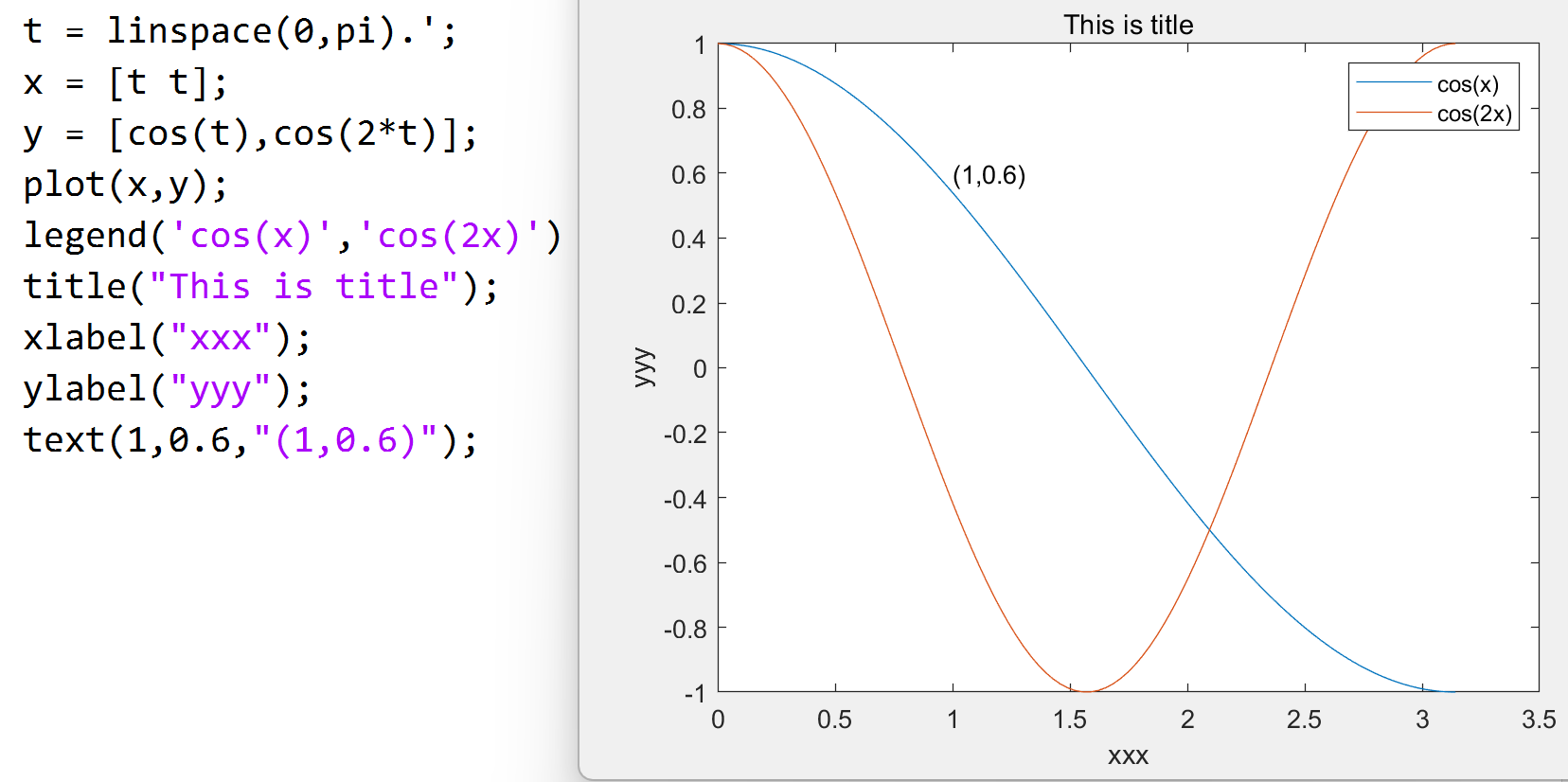
axis 函数控制坐标轴
grid on/off 开关网格线
hold on/off 控制保持原有图形或刷新图形窗口

三维绘图

plot3(x,y,z) 与 fplot3(x,y,z) 函数, 和二维类似

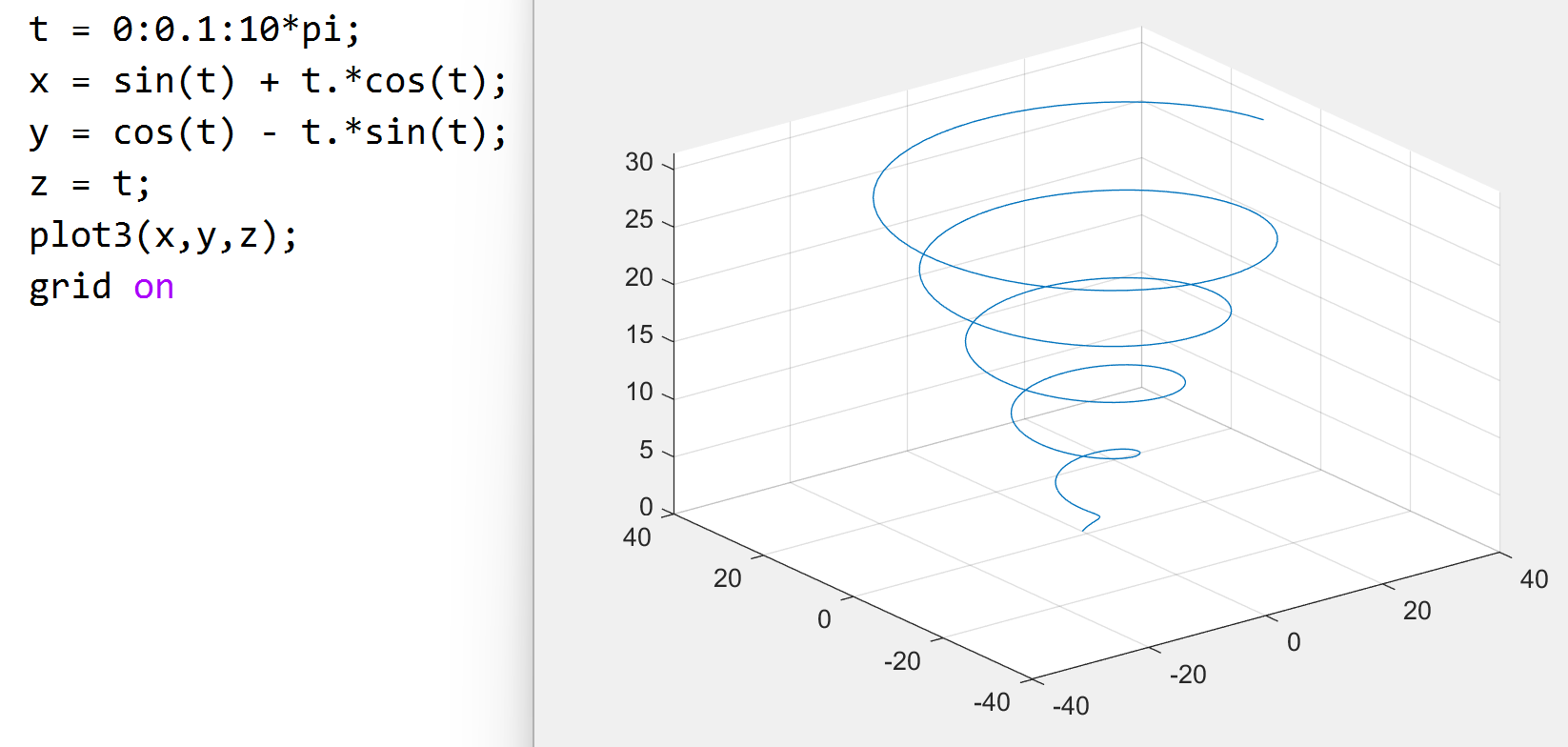
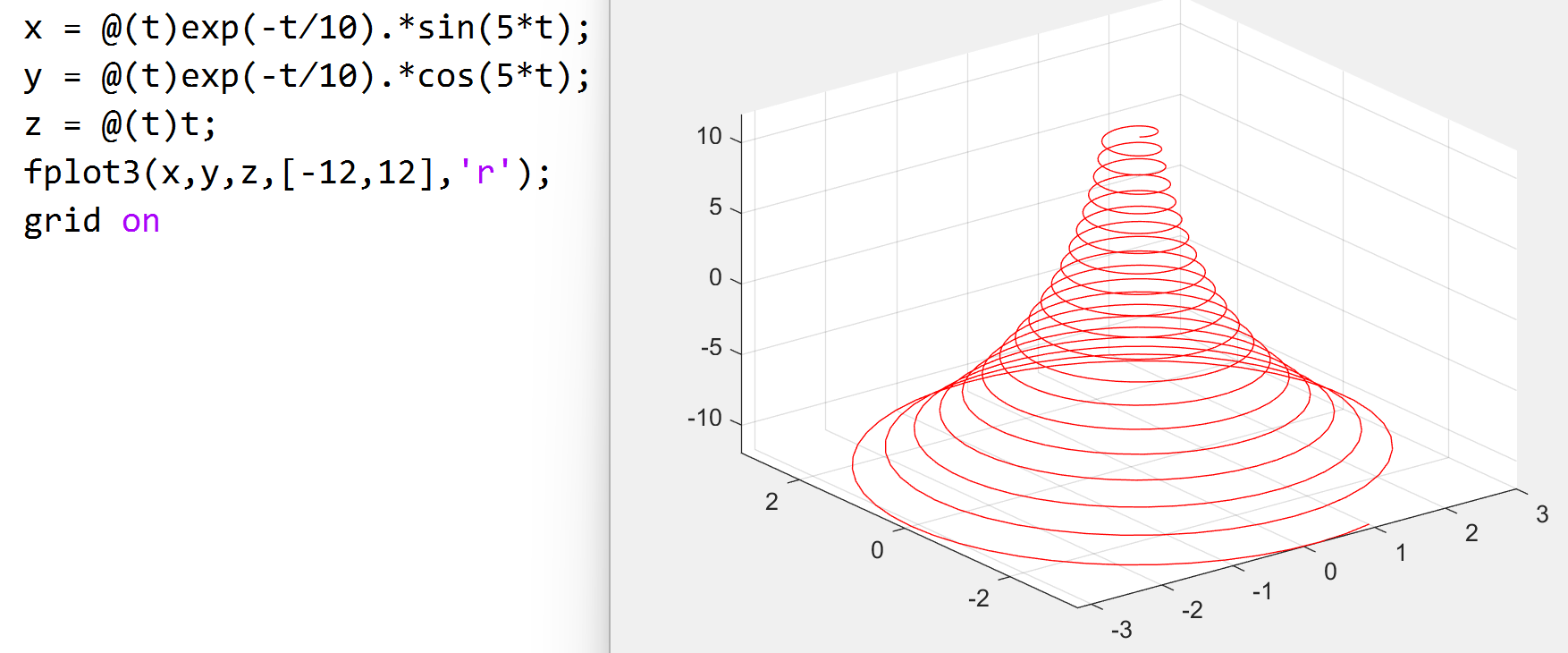
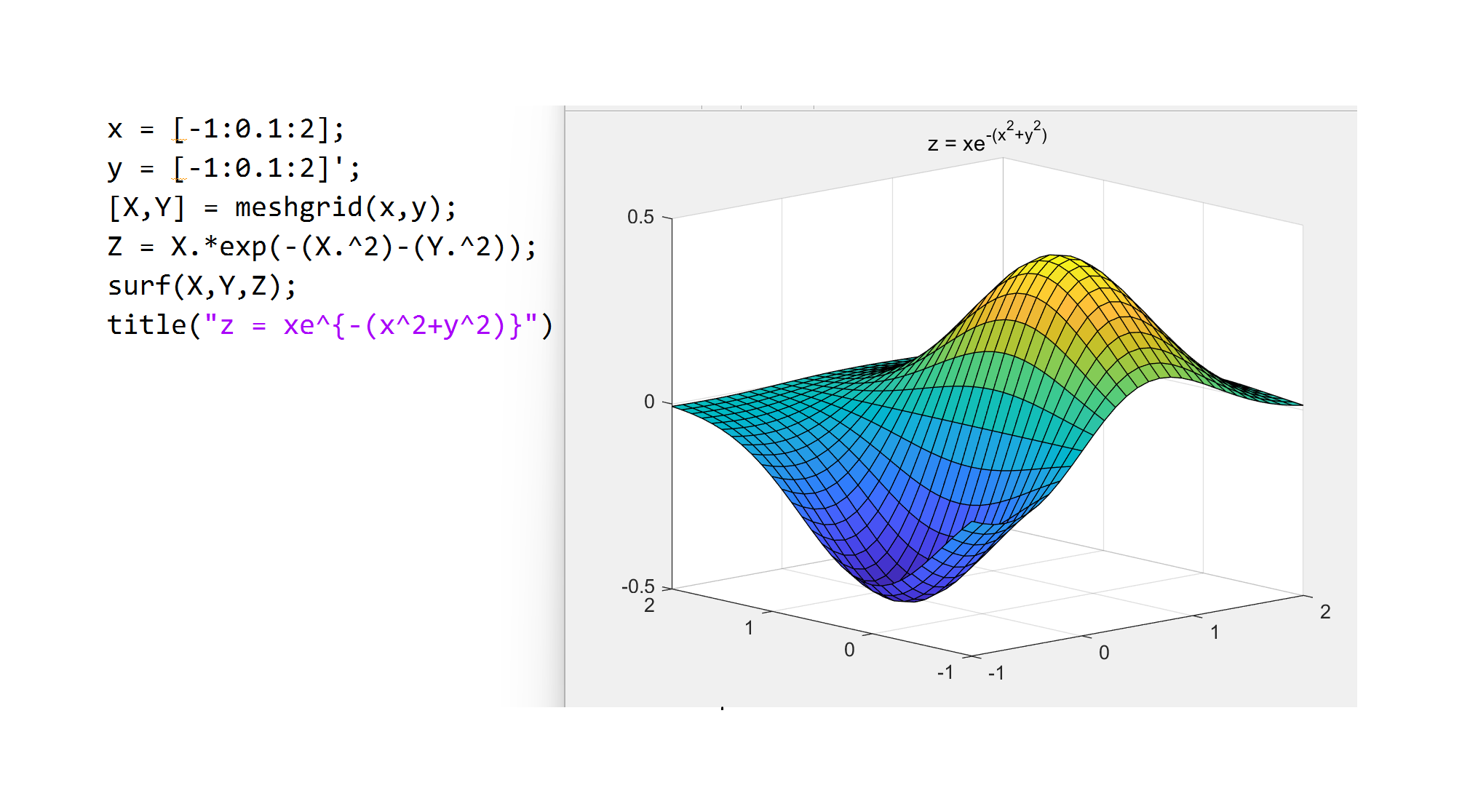
三维曲面

先生成网格坐标矩阵 [X,Y] = meshgrid(x,y)
然后 mesh(X,Y,Z,c) 或 surf(X,Y,Z,c) 绘制曲面, 其中 c 指定曲面颜色, 默认正比于曲面高度

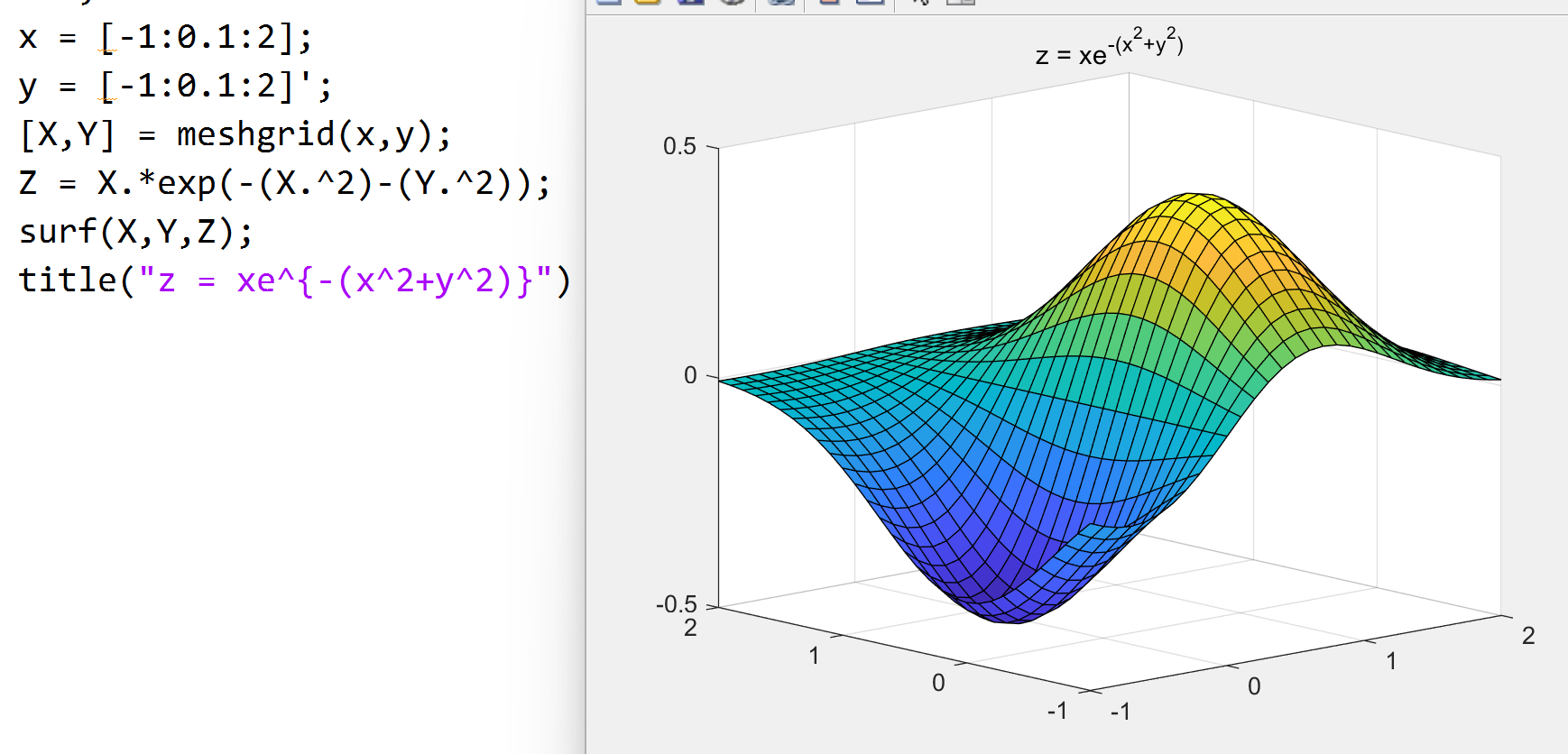
句柄与窗口

句柄: 可以理解为图像的别名, 设 h = plot(x,y)
get(h) 获取图像属性, set(h) 更改图像 eg. set(h,'Color','red')

子图: 同一图形窗口中的不同坐标系下的图形为子图
subplot(m,n,p) 将图形窗口划分为 m*n 个活动区, p 指定当前活动区

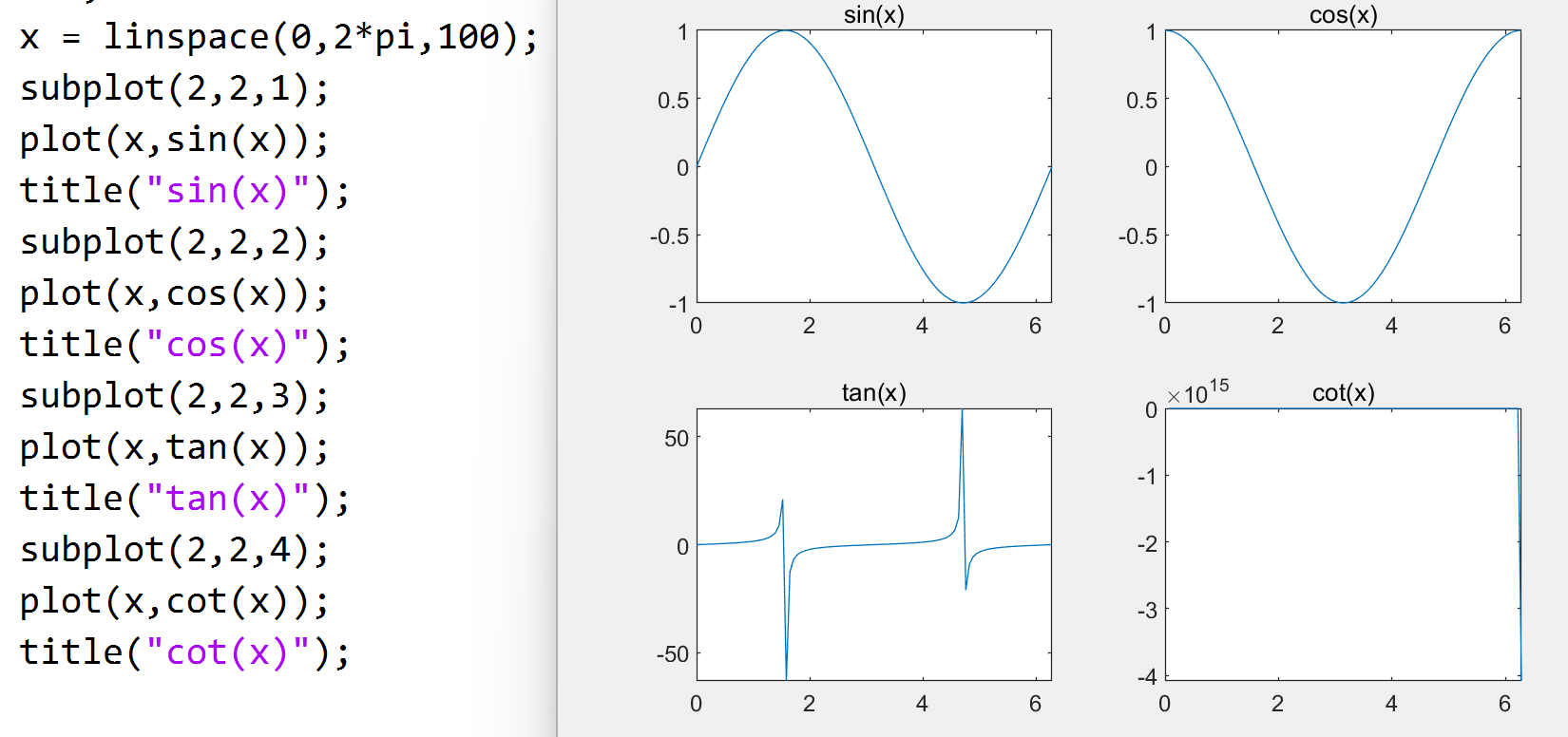
subplot(m,n,p) 下方区域的图形属性设置全都属于当前子图

MCM/ICM Matlab

使用 `optimproblem` 创建和求解优化问题

可以求解线性和非线性规划问题
语法:

1 2	prob = optimproblem prob = optimproblem(Name,Value)

x = optimvar(name) 创建标量优化变量。优化变量是符号对象, 可以使用它来为目标函数和问题约束创建表达式
x = optimvar(name,n) 创建由优化变量组成的 n×1 向量

在问题中设置一个目标函数: prob.Objective = x'*a*x
在问题中创建线性不等式约束: prob.Constraints.con = sum(x.^2)==1
检查问题: show(prob)
求解, sol = solve(prob), sol.x 就是答案
\[ 已知矩阵 A = \begin{bmatrix} 1 & 4 & 5 \\ 4 & 2 & 6 \\ 5 & 6 & 3 \end{bmatrix} , x= \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} , 求二次型 f(x_1,x_2,x_3) = \mathbf{x^T Ax}\; \\ 在单位球面 x_1^2+x_2^2+x_3^2=1 上的最小值 \]

可以证明其答案等于 $A$ 的最小特征值
可以把其问题归结为如下的非线性规划问题(s.t. = subject to):
\[ 求\;min \;\mathbf{x^T Ax},\;\newline s.t.=\left\{ \begin{matrix} x_1^2+x_2^2+x_3^2=1, \\ x_i \in R,\;\;i=1,2,3 \end{matrix} \right. \]

clc; clear; format long;
a=[1 4 5;4 2 6;5 6 3];
val = eig(a);
minv = min(val);
prob = optimproblem; 
x = optimvar('x',3); # 3 个变量
prob.Objective = x'*a*x;
prob.Constraints.con = sum(x.^2)==1;
x0.x=rand(3,1); % 非线性就要设置 x0 初值扔进去
[sol,fval,flag,out] = solve(prob,x0),sol.x;
fval, sol.x
#----------------------------------------
fval = -3.66868
ans = 
	-0.31298
	-0.57734
	 0.75412

\[ 求\;max\;z=2x_1+3x_2-5x_3, \;\newline s.t.= \left\{\begin{matrix} x_1+x_2+x_3=7, \\ 2x_1-5x_2+x_3\geq 10, \\ x_1+3x_2+x_3 \leq 12, \\ x_1, x_2, x_3 \geq 0. \end{matrix}\right. \]

clc; clear;
prob = optimproblem('ObjectiveSense','max'); % 指定最大化 objective
x = optimvar('x',3,'LowerBound',0); % 设置变量下限为 0 
prob.Objective = 2*x(1)+3*x(2)-5*x(3);
prob.Constraints.c1 = x(1)+x(2)+x(3)==7;
prob.Constraints.c2 = 2*x(1)-5*x(2)+x(3)>=10;
prob.Constraints.c3 = x(1)+3*x(2)+x(3)<=12;
[sol, fval, flag, out] = solve(prob), sol.x;
fval, ans
#---------------------------------------
fval = 14.5714
ans = 
	6.4286
	0.5714
	0

设置 optimproblem('Type','integer') 可以解决整数的线性规划问题

遗传算法(Genetic Algorithm)

在上文的基础上还可以求解非线性整数线性规划

遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题, 一定数量的候选解 (称为个体) 可抽象表示为染色体, 使种群向更好的解进化。传统上, 解用二进制表示 (即 0 和 1 的串), 但也可以用其他表示方法。进化从完全随机个体的种群开始, 之后一代一代发生。在每一代中评价整个种群的适应度, 从当前种群中随机地选择多个个体 (基于它们的适应度), 通过自然选择和突变产生新的生命种群, 该种群在算法的下一次迭代中成为当前种群。

在遗传算法里, 优化问题的解被称为个体, 它表示为一个变量序列, 叫做染色体或者基因串。染色体一般被表达为简单的字符串或数字符串, 不过也有其他的依赖于特殊问题的表示方法适用, 这一过程称为编码。首先, 算法随机生成一定数量的个体, 有时候操作者也可以干预这个随机产生过程, 以提高初始种群的质量。在每一代中, 都会评价每一个体, 并通过计算适应度函数得到适应度数值。按照适应度排序种群个体, 适应度高的在前面。这里的“高”是相对于初始的种群的低适应度而言。

下一步是产生下一代个体并组成种群。这个过程是通过选择和繁殖完成, 其中繁殖包括交配 (crossover, 在算法研究领域中我们称之为交叉操作) 和突变 (mutation)。选择则是根据新个体的适应度进行, 但同时不意味着完全以适应度高低为导向, 因为单纯选择适应度高的个体将可能导致算法快速收敛到局部最优解而非全局最优解, 我们称之为早熟。作为折中, 遗传算法依据原则: 适应度越高, 被选择的机会越高, 而适应度低的, 被选择的机会就低。初始的数据可以通过这样的选择过程组成一个相对优化的群体。之后, 被选择的个体进入交配过程。一般的遗传算法都有一个交配概率 (又称为交叉概率), 范围一般是0.6~1, 这个交配概率反映两个被选中的个体进行交配的概率。例如, 交配概率为0.8, 则80%的“夫妻”会生育后代。每两个个体通过交配产生两个新个体, 代替原来的“老”个体, 而不交配的个体则保持不变。交配父母的染色体相互交换, 从而产生两个新的染色体, 第一个个体前半段是父亲的染色体, 后半段是母亲的, 第二个个体则正好相反。不过这里的半段并不是真正的一半, 这个位置叫做交配点, 也是随机产生的, 可以是染色体的任意位置。再下一步是突变, 通过突变产生新的“子”个体。一般遗传算法都有一个固定的突变常数 (又称为变异概率), 通常是0.1或者更小, 这代表变异发生的概率。根据这个概率, 新个体的染色体随机的突变, 通常就是改变染色体的一个字节 ( 0 变到 1 , 或者 1 变到 0 )。

经过这一系列的过程 (选择、交配和突变), 产生的新一代个体不同于初始的一代, 并一代一代向增加整体适应度的方向发展, 因为总是更常选择最好的个体产生下一代, 而适应度低的个体逐渐被淘汰掉。这样的过程不断的重复: 评价每个个体, 计算适应度, 两两交配, 然后突变, 产生第三代。周而复始, 直到终止条件满足为止。

~~以上内容没有任何意义, 你只要会掉包就行~~

ga 函数:
x = ga(fitnessfcn,nvars,A,b,[],[],LB,UB,nonlcon,IntCon,options)
fitnessfcn 为适应目标函数
nvars 为目标函数自变量的个数
$A$ 与 $b$ : 线性不等式约束 $A * x b $ 中的矩阵
$Aeq$ 与 $beq$ : 线性等式约束 $Aeq * x = beq $ 中的矩阵
nonlcon: 非线性约束, 该函数返回两个输出, 即: [g,h] = nonlcon(x) , g 为非线性不等式约束, 所有的不等式约束均以列向量的形式存在变量 g 中。h为非线性等式约束, 也以列向量的形式存储
LB UB 为下界和上界
IntCon: 若变量 x 中存在整数变量, 则在这里设置, 指定这些下标的变量都是整数变量
options: 调整种群规模, 迭代次数等
\[ 求解下列问题: max\;z = x_1^2+x_2^2+3x_3^2+4x_4^2+2x_5^2-8x_1-2x_2-3x_3-x_4-2x_5,\newline \]

\[ s.t.= \left\{\begin{matrix} 0 \leq x_i \leq 99, 且 x_i 为整数(i=1,2,\cdots, ),\\ x_1+x_2+x_3+x_4+x_5 \leq 400, \\ x_1 +2x_2+2x_3+x_4+6x_5 \leq 800, \\ 2x_1+x_2+6x_3 \leq 200, \\ x_3+x_4+5x_5 \leq 200. \end{matrix}\right. \]

\[ sol.\;构造矩阵 A = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 2 & 1 & 6 \\ 2 & 1 & 6 & 0 & 0 \\ 0 & 0 & 1 & 1 & 5 \end{bmatrix} , b = \begin{bmatrix} 400 \\ 800 \\ 200 \\ 200 \end{bmatrix} , 有 Ax \leq b \]

clc; clear;
c1 = [1,1,3,4,2]; c2=[-8,-2,-3,-1,-2]; 
obj = @(x) -sum(c1.*x.^2 + c2.*x); % 目标函数取反, 因为默认求最小值
a = [1,1,1,1,1;1,2,2,1,6
    2,1,6,0,0;0,0,1,1,5]; 
b = [400,800,200,200]';
[x,f,flag,out] = ga(obj,5,a,b,[],[],zeros(1,5),99*ones(1,5),[],[1:5]);
x, f
#-------------------------------
x = 50 99 0 99 20
f = -51568 #ans = 51568

ga(obj,5,a,b,[],[],zeros(1,5),99*ones(1,5),[],[1:5]) 调用遗传算法 ga 来求解优化问题。
具体参数含义如下：

obj: 目标函数，表示要优化的目标。
5: 决策变量的数量，即 x 向量的长度为 5。
a: 线性约束的系数矩阵。
b: 线性约束的右侧值。
[]: 这两个空的方括号表示没有等式约束（默认为空）。
zeros(1,5): 决策变量的下限，这里是 [0, 0, 0, 0, 0]，即所有变量的最小值为 0。
99*ones(1,5): 决策变量的上限，这里是 [99, 99, 99, 99, 99]，即所有变量的最大值为 99。
[]: 不指定选择交叉和变异的具体方式。
[1:5]: 遗传算法中每个决策变量都是整数变量。

[x,f,flag,out] = ... 使用遗传算法并将其返回结果赋值给四个输出变量：

x: 最优解，即求解的决策变量的值。
f: 最优解对应的目标函数值。
flag: 结束条件的标志，指示算法结束的原因。
out: 包含优化过程的其他信息，如迭代次数、每代最好的适应度等。

\[ eg. 求 \; x+10sin(5x)+7cos(4x) \; 的最大值 \]

clc; clear;
obj = @(x) -(x+10*sin(5*x)+7*cos(4*x)); 
[x,f,flag,out] = ga(obj,1,[],[],[],[],5,10,[],[]);
x, f
%--------------------------------
x = 7.8567
f = -24.8554 % ans = 24.8554

蒙特卡洛法

应用: 算面积、超越积分数值计算、不规则图形面积、风险评估
unifrnd(): r = unifrnd(a,b) 从具有下部端点 a 和上部端点 b 的连续均匀分布中生成一个随机数
r = unifrnd(a,b,sz) 生成一个均匀 [a,b] 间随机数数组，其中大小向量 sz 指定 size(r)

sz = [2 3];
r2 = unifrnd(0,1,sz)
%--------------------------------
r2 = 
	0.0975    0.5469    0.9649
    0.2785    0.9575    0.1576

计算 $y = x^2$ 和 $y = 12-x$ 与 $x$ 轴在第一象限围成的曲边三角形的面积

clc; clear; n=10^8;
x = unifrnd(0,12,[1,n]); y = unifrnd(0,9,[1,n]);
frequency = sum(y<x.^2 & x<=3) + sum(y<12-x & x>=-3);
area = 12*9*frequency/n
%--------------------------------
area = 76.5024

计算 $y = sin(x^2), y = \frac{sin(x)}{x}$ 和 $y = e^{-x^2}$ 在 $x \in [0,2]$ 上的面积

clc; clear; n=10^6; hold on;
y1 = @(x) sin(x.^2);
y2 = @(x) sin(x)./x;
y3 = @(x) exp(-(x.^2)); 
x = unifrnd(0,2,[1,n]);
y = unifrnd(0,1,[1,n]);
frequency = sum(y>=y3(x) & y<=y2(x) & y<=y1(x))
area = 1*2*frequency/n
%--------------------------------
area = 0.4190

图论绘图

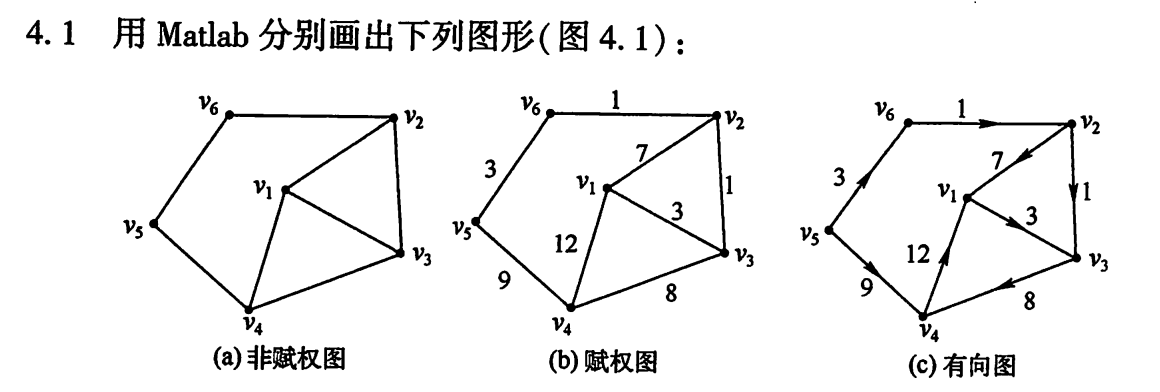
clc; clear;
a1 = zeros(6); 
a1(1,[2:4])=1; a1(2,[3,6])=1; a1(3,4)=1; a1(4,5)=1; a1(5,6)=1;
s = cellstr(strcat('v',int2str([1:6]')));
G1 = graph(a1,s,'upper');
plot(G1,'Layout','circle','NodeFontSize',12)

a2 = zeros(6);
a2(1,[2:4])=[7,3,12]; a2(2,[3,6])=1; a2(3,4)=8; a2(4,5)=9; a2(5,6)=3;
G2 = graph(a2,s,'upper'); figure;
plot(G2,'Layout','circle','EdgeLabel',G2.Edges.Weight)

a3 = zeros(6);
a3(1,3)=3; a3(2,[1,3])=[7,1]; a3(3,4)=8; a3(4,1)=12; a3(5,[4,6])=[9,3]; a3(6,2)=1;
G3 = digraph(a3,s); figure;
plot(G3,'EdgeLabel',G3.Edges.Weight,'Layout','circle')

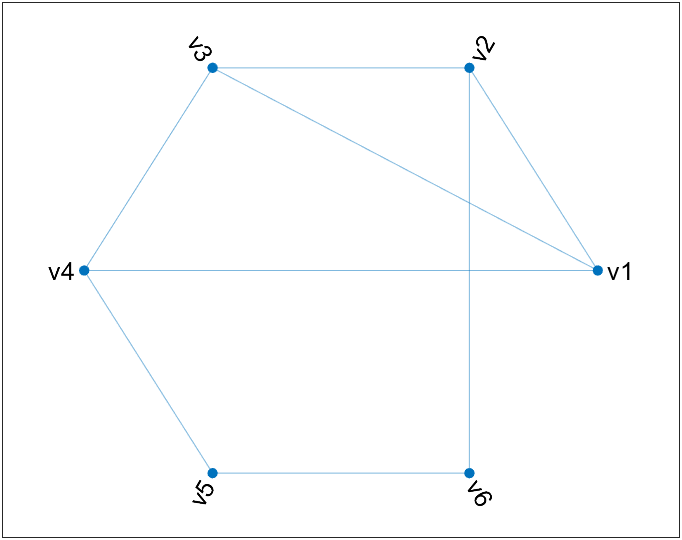
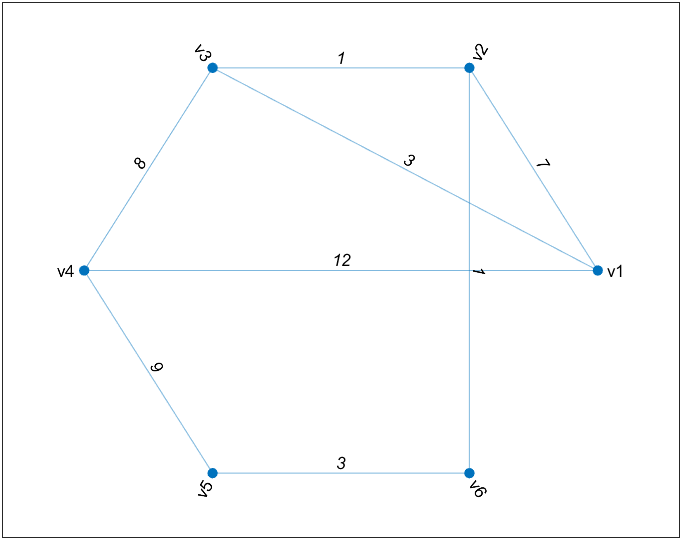
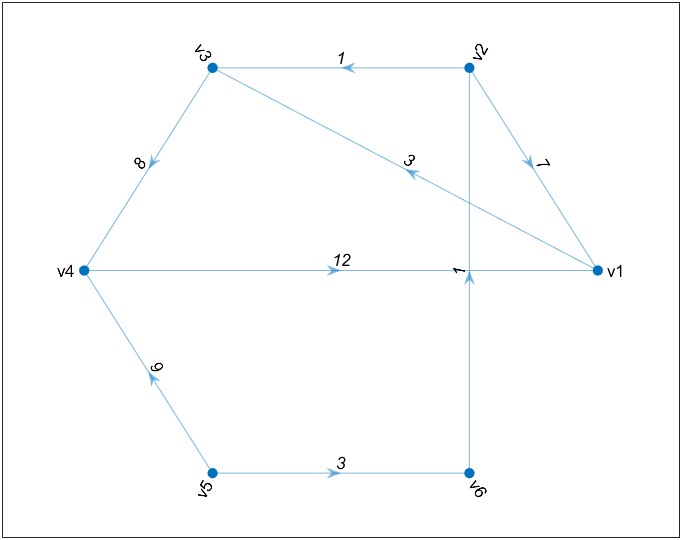
旅行商问题(TSP)

用图论的术语说, 就是在一个赋权完全图中, 找出一个有最小权的 Hamilton 圈。称这种圈为最优圈
一个可行的办法是首先求一个 Hamilton 圈 C, 然后适当修改 C 以得到具有较小权的另一个 Hamilton 圈。修改的方法叫做改良圈算法:
设初始圈 $C = v_1v_2 \cdots v_nv_1$
对于 $1 \leq i < i+1 < j \leq n$, 构造新的 Hamilton 圈
\[ C_{ij} = v_1v_2 \cdots v_i \underline{v_j v_{j-1} v_{j-2} \cdots v_{i+1}}_{(reverse)} v_{j+1} v_{j+2} \cdots v_n v_1 \] 它是由 $C$ 中删去边 $v_iv_{i+1}$ 和边 $v_jv_{j+1}$ , 添加边 $v_iv_j$ 和边 $v_{i+1}v_{j+1}$ 得到的。若:
\[ w(v_iv_j) + w(v_{i+1}v_{j+1}) < w(v_iv_{i+1}) + w(v_jv_{j+1}), \] 则以 $C_{ij}$ 代替 $C$ , $C_{ij}$ 叫做 $C$ 的改良圈
重复以上过程, 在无法改进后停止算法, 可以选择不同的初始圈多进行几次得到更好结果

eg. 对下图六城市找最小权的 Hamilton 圈

	L	M	N	Pa	Pe	T
L		56	35	21	51	60
M	56		21	57	78	70
N	35	21		36	68	68
Pa	21	57	36		51	61
Pe	51	78	68	51		13
T	60	70	68	61	13

有初始圈 5->1->2->3->4->6->5, 长度为 274, 代码见下:

clc, clear; % 旅行商问题简单来说就是计算出发地经过若干地点再返回原地的最短路径
% 这个程序围绕数学建模书 59 页问题,从地点 5 开始出发，最后再回到地点 5
a=zeros(6);  % 初始化邻接矩阵
a(1,2)=56; a(1,3)=35; a(1,4)=21; a(1,5)=51; a(1,6)=60;
a(2,3)=21; a(2,4)=57; a(2,5)=78; a(2,6)=70; a(3,4)=36; a(3,5)=68; a(3,6)=68;
a(4,5)=51; a(4,6)=61; a(5,6)=13; % 对邻接矩阵进行赋值
a=a+a';% 利用对称矩阵的性质获得最终得邻接矩阵
L=size(a,1); % 获取矩阵的行数，如果是size(a,2)就是获取矩阵的列数
c=[5 1:4 6 5];  % 这样写是为了方便，实际上c=[5 1 2 3 4 6 5],这个定义的是初始圈
[circle,long]=modifycircle(a,L,c); % 调用下面的修改圈的子函数
circle, long  % 注意如果在变量名后面加上分号的话就不会在窗口显示它的值，如果想显示值就不要加分号
function [circle,long] = modifycircle(a,L,c)
    for k=1:L  % 因为要走过六个地方，于是要遍历循环
        flag=0;    % 预先设置是否知道已经修改了边,如果循环后flag还是0，说明并没有修改初始圈
        long=0;    % 初始化总路程
        for m=1:L-2  % 因为算法中的i是1<=i<i+1<j<=n,i与n最少差2
            for n=m+2:L % 原算法中的j是至少比i大2的
                if a(c(m),c(n))+a(c(m+1),c(n+1))<a(c(m),c(m+1))+a(c(n),c(n+1)) 
                % 如果修改后的新圈比旧圈权重小
                    c(m+1:n)=c(n:-1:m+1);  % 将原来的路线倒过来，结合上面讲解的算法
                    flag=flag+1; % 如果修改了圈就将flag的值加1
                end
            end
        end
        if flag==0  % 如果循环结束后都没有修改圈的话
            long=274 % 那么所走路线就是初始圈，路程就是初始路线的总路程
        else
            for i=1:L
                long=long+a(c(i),c(i+1)) % 遍历更新总路程
            end
            circle=c; % 更新路线圈
            return 
            % 在条件块（例如 if 或 switch）或循环控制语句（例如 for 或 while）使用 return 时需要小心。当 MATLAB 到达 return 语句时，它并不仅是退出循环，还退出脚本或函数，并将控制权交还给调用程序或命令提示符。
        end
    end
end
%-------------------------------
circle = 5 4 1 3 2 6 5
long = 211

你也可以用 0-1 整数规划模型解决 TSP 问题, 只要引进这样的 0-1 变量:
\[ x_{ij} = \left\{\begin{aligned} 1, \;\;&当最短路径经过\;i\;到\;j\;的边时\\ 0, \;\;&当最短路径不经过\;i\;到\;j\;的边时 \end{aligned}\right. \] 然后目标是要求一个 $min \; z = \sum\limits_i\sum\limits_j w_{ij} x_{ij}$ 这样的东西, 主要约束 $x_{ij}$

插值

拉格朗日插值和牛顿插值只有理论上意义, 实际应用不大, 故略去

分段线性插值

直接把 x, y 散点拿 plot 一画就可以了, 略

三次样条插值

在给定两点间的表达式均为一个三次多项式, 在整个区间上有连续的二阶导数
用 spline 函数, s = spline(x,y,xq) 返回与 xq 中的查询点对应的插值向量 s。s 的值由 x 和 y 的三次样条插值确定。
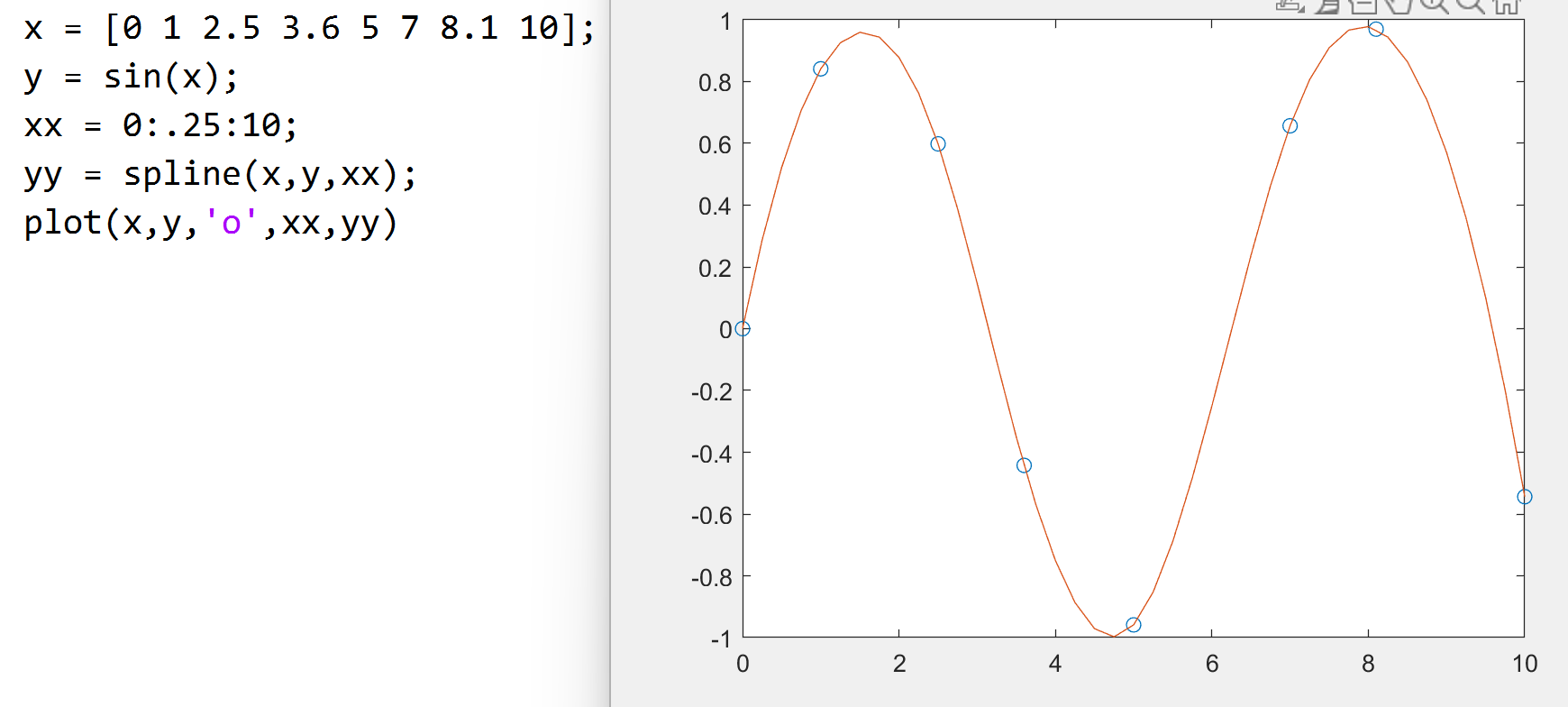
eff50bbb118a1685f62896f56a7dce6f

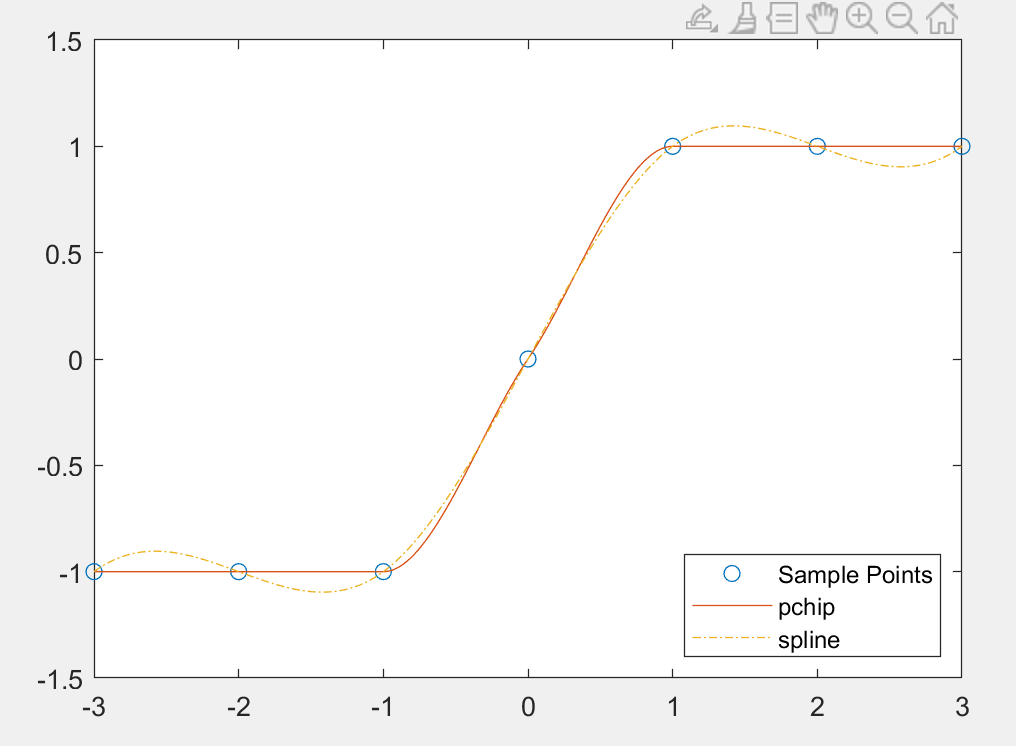
pchip 分段三次插值

用多项式作插值函数, 随着插值节点(或插值条件)的增加, 插值多项式次数也相应增加, 高次插值不但计算复杂且往往效果不理想, 甚至可能会产生龙格振荡现象。

利用多项式对某一函数作近似逼近, 计算相应的函数值, 一般情况下, 多项式的次数越多, 需要的数据就越多, 而预测也就越准确。然而, 插值次数越高, 会产生插值结果越偏离原函数的现象, 这称为龙格振荡现象。

分段插值就没这问题了

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:0.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.')
legend('Sample Points','pchip','spline','Location','SouthEast')

griddedInterpolant 函数

我勒个超级插值函数
F = griddedInterpolant(X1,X2,...,Xn,V) 使用作为一组 n 维数组 X1,X2,...,Xn 传递的样本点的完整网格创建二维、三维或 N 维插值。V 数组包含与 X1,X2,...,Xn 中的点位置关联的样本值。每个数组 X1,X2,...,Xn 的大小都必须与 V 相同。
F = griddedInterpolant(___,Method) 指定插值方法:
'linear'、'nearest'、'next'、'previous'、'pchip'、'cubic'、'makima' 或 'spline'
你可以在上述任意语法中指定 Method 作为最后一个输入参量。

计算对应的函数值的使用格式为 vq = F(xq1,xq2,...,xqn)

x = -5:0.8:5;  
y = x';
z = sin(x.^2 + y.^2) ./ (x.^2 + y.^2);
F = griddedInterpolant({x,y},z); %二维, (x,y) 点, z 为函数值
xq = -5:0.1:5;
yq = xq';
vq = F({xq,yq}); % 把原来 0.8 的步长插值成 0.1 的
surf(xq,yq,vq)

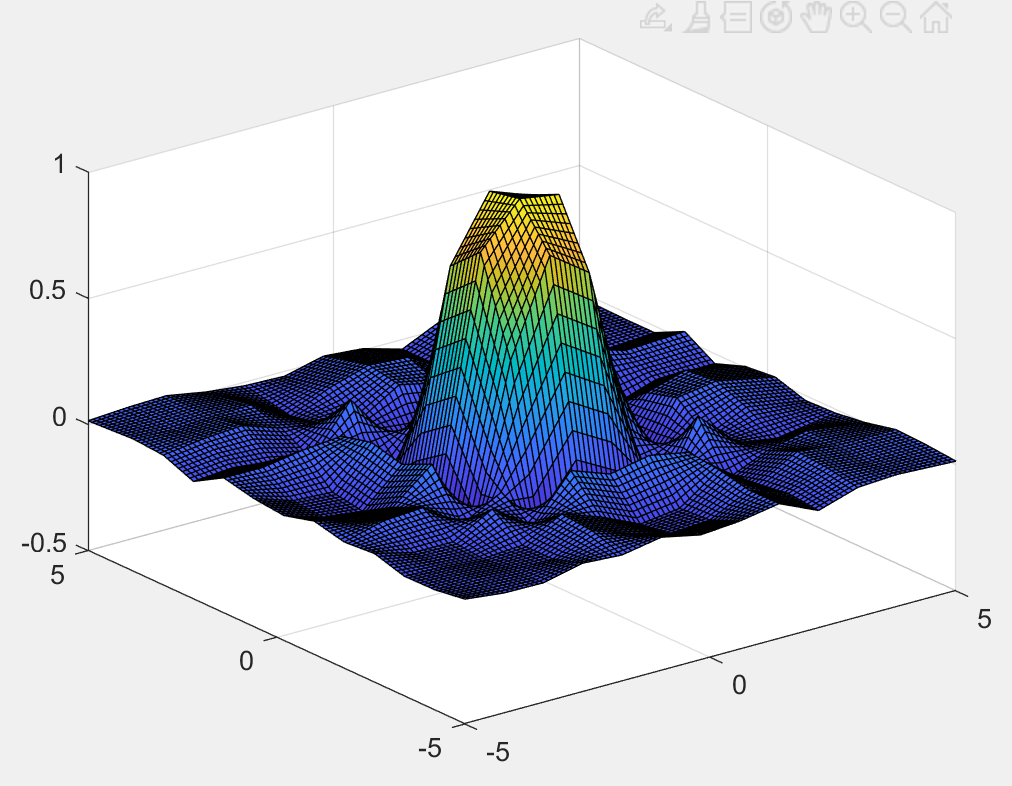
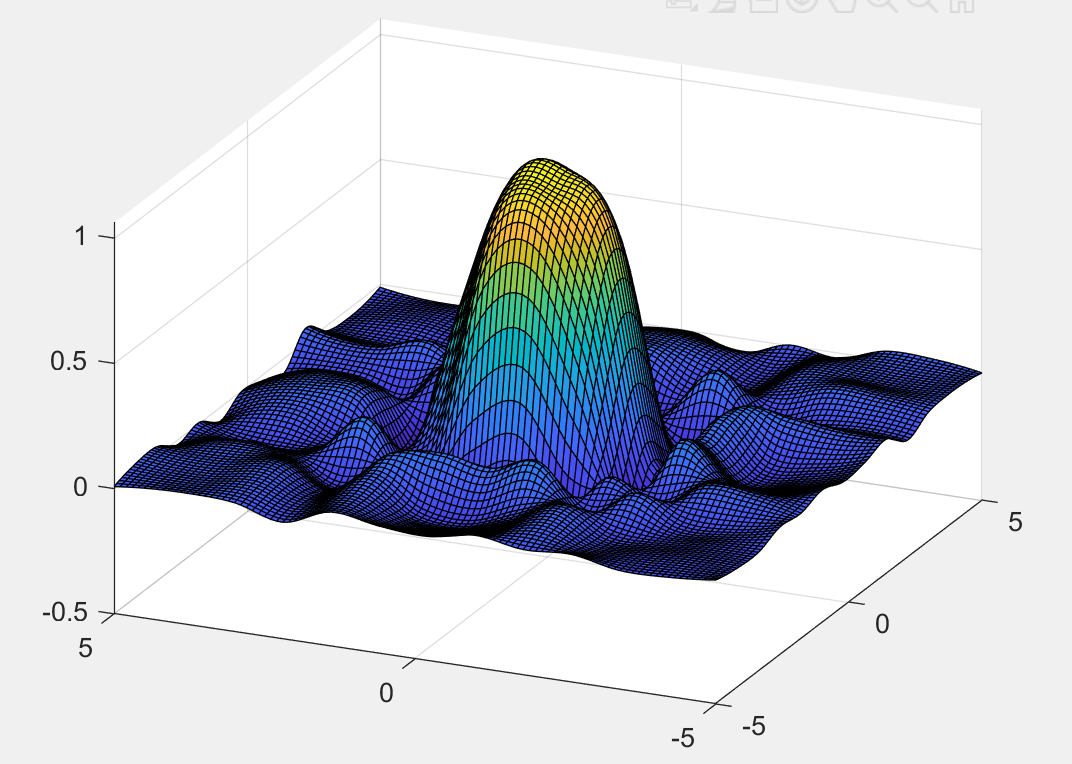
如果改为 F = griddedInterpolant({x,y},z,'cubic') , 能获得更好的三次插值

拟合

最小二乘法

先看线性的, 根据一些基础的线性代数知识, $\mathbf{A^T Ax= A^T b}$ 肯定有解, 故 $\mathbf{x} = \mathbf{(A^T A)^{-1} A^T b}$ 为所求的拟合矩阵的系数, $f(x) = \displaystyle \sum a_ix^i$
我们还是直接套库, 就不自己写了
p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数, 该阶数是 y 中数据的最佳拟合 (基于最小二乘指标)。p 中的系数按降幂排列, p 的长度为 n+1，其中 $p(x) = p_1x^n + p_2x^{n-1} + \dots + p_nx + p_{n+1}$

y = polyval(p,x) 计算多项式 p 在 x 的每个点处的值

x = [0:7];
y = [27,26.8,26.5,26.3,26.1,25.7,25.3,24.8];
p = polyfit(x,y,1);
x1 = linspace(0,7);
y1 = polyval(p,x1);
hold on;
plot(x,y,'o');
plot(x1,y1);

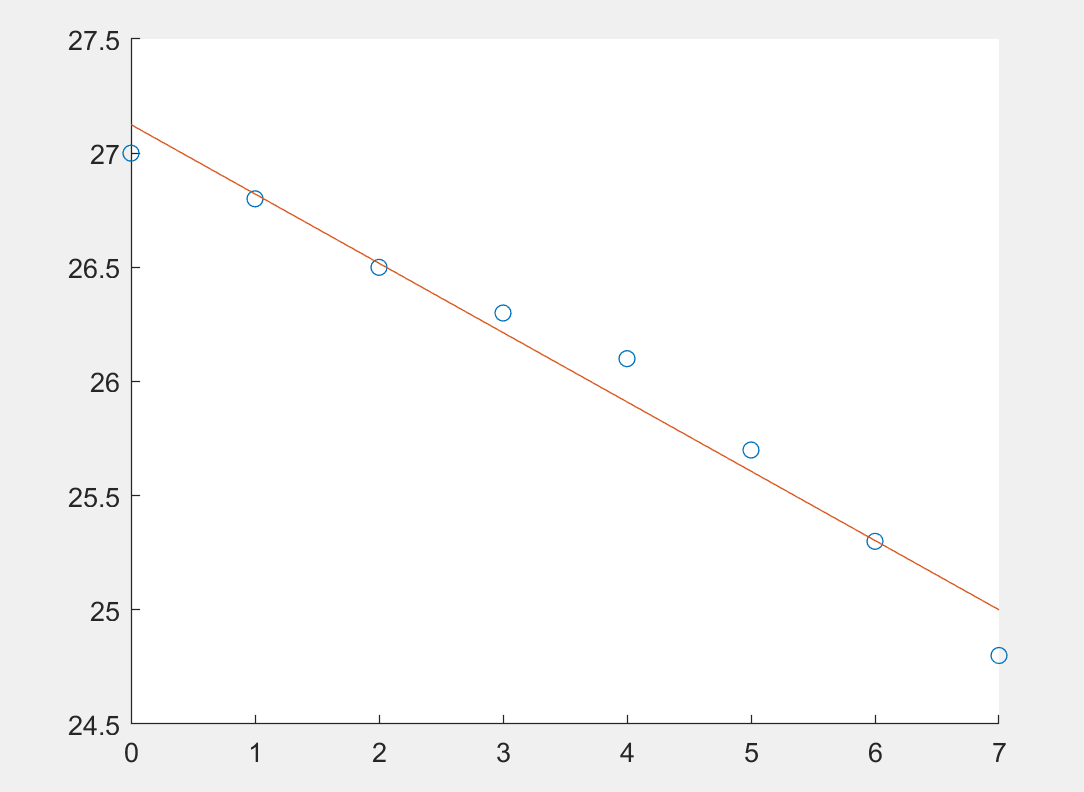
若样本点不是线性的, 我们可以尝试用常见的非线性函数来拟合, 例如多项式、双曲线 $y= \displaystyle \frac{a_1}{x}+a_2$、指数曲线 $y = a_1 e^{a_2x}$
我们这次不用库了, 用工具箱！
Matlab - APP - Curve Fitting Tool 进入, Polynomial, Power, Sum of Sine, Logistic(S 型) 等多种拟合方式任君挑选

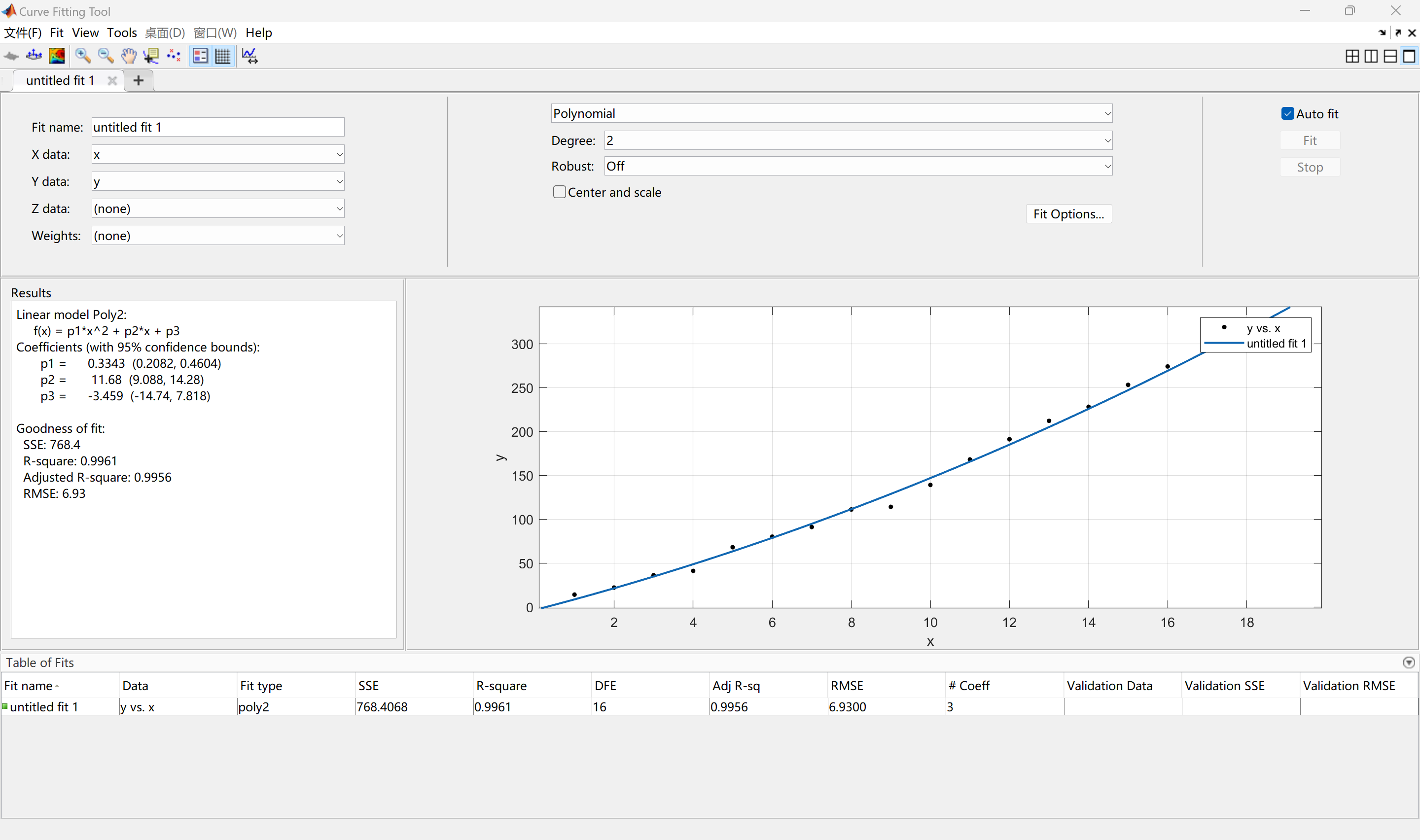
线性前提下, $R^2$ 越接近 1 越好, 否则 SSE 越低越好
做题可以先把散点图画出来, 分段拟合

微分方程

解析解

调库，调库！
$eg. 解 \;\;y'' + 2y' +y-x^2 =0, y(0)=0, y'(0)=15$

1
2
3

y=dsolve('D2y+2*Dy+y-x^2=0','y(0)=0','Dy(0)=15','x')
%---------------------------
y = 13*x*exp(-x) - 6*exp(-x) - 4*x + x^2 + 6

其中 Dty 代表 $y^{(t)}$, 格式为 y = dsolve('f1','f2',...,'x')
你也可以:

syms y(x) % 定义符号变量, 说明 y 是 x 的函数
eq = y - diff(y,x) == 2*x; % diff(y,x) = dy/dx = y'
dsolve(eq) % 通解
dsolve(eq,y(0)==3) % 特解
%----------------------------
ans = 2*x + C1*exp(x) + 2
ans = 2*x + exp(x) + 2

\[ eg.\;求 \left\{\begin{aligned} &\frac{dx}{dt} = y \\ &\frac{dy}{dt} = -x \end{aligned}\right. \;\;且 \;x(0)=0, y(0)=1\;的解 \]

syms x(t) y(t) % 定义两个符号变量
eq1 = diff(x,t) == y;
eq2 = diff(y,t) == -x;
eqs = [eq1 eq2]; % 方程矩阵
cond = [x(0)==0, y(0)==1]; % 条件矩阵
[xsol(t),ysol(t)] = dsolve(eqs,cond)
%------------------------------
xsol(t) = sin(t)
ysol(t) = cos(t)

求不出解析解, 就去求数值解, ode45, 启动！

数值解

ode45 可以求解非刚性问题(函数变化缓慢) (刚性问题用 ode15s )
格式为: [t,y] = ode45(odefun,tspan,y0)
其中 odefun 是用匿名函数定义 $f(t,y)$ 的函数文件名(或匿名函数返回值), tspan = [t0 tf] 为一个积分区间, 奇妙的 matlab 会自动选择步长并求经过的点集的数值解, 你可以之后 plot 把图象画出来, y0 为初始条件, 长度与 odefun 的输出长度相同
ode45 只能解一阶微分方程, 高阶的要先拆成一阶微分方程组

eg. 解 $y_1'' - \mu(1-y_1^2)y_1'+y_1 = 0,\;其中\; \mu=1, y_1(0)=2, y_1'(0)=0$
设 $y_1' = y_2$ 有 $y_1' = y_2, \;y_2'=\mu(1-y_1^2)y_2-y_1$

clc; clear; 
[x y] = ode45(@(x,y) df(x,y),[0,20],[2,0]); %调用时导参, 再套一层匿名函数
plot(x,y(:,1),'-o',x,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE45');
xlabel('Time t'); ylabel('Solution y'); legend('y_1','y_2');
function dydt = df(x,y)
    dydt = zeros(2,1);
    dydt(1) = y(2);
    dydt(2) = (1-y(1)^2)*y(2)-y(1);
end

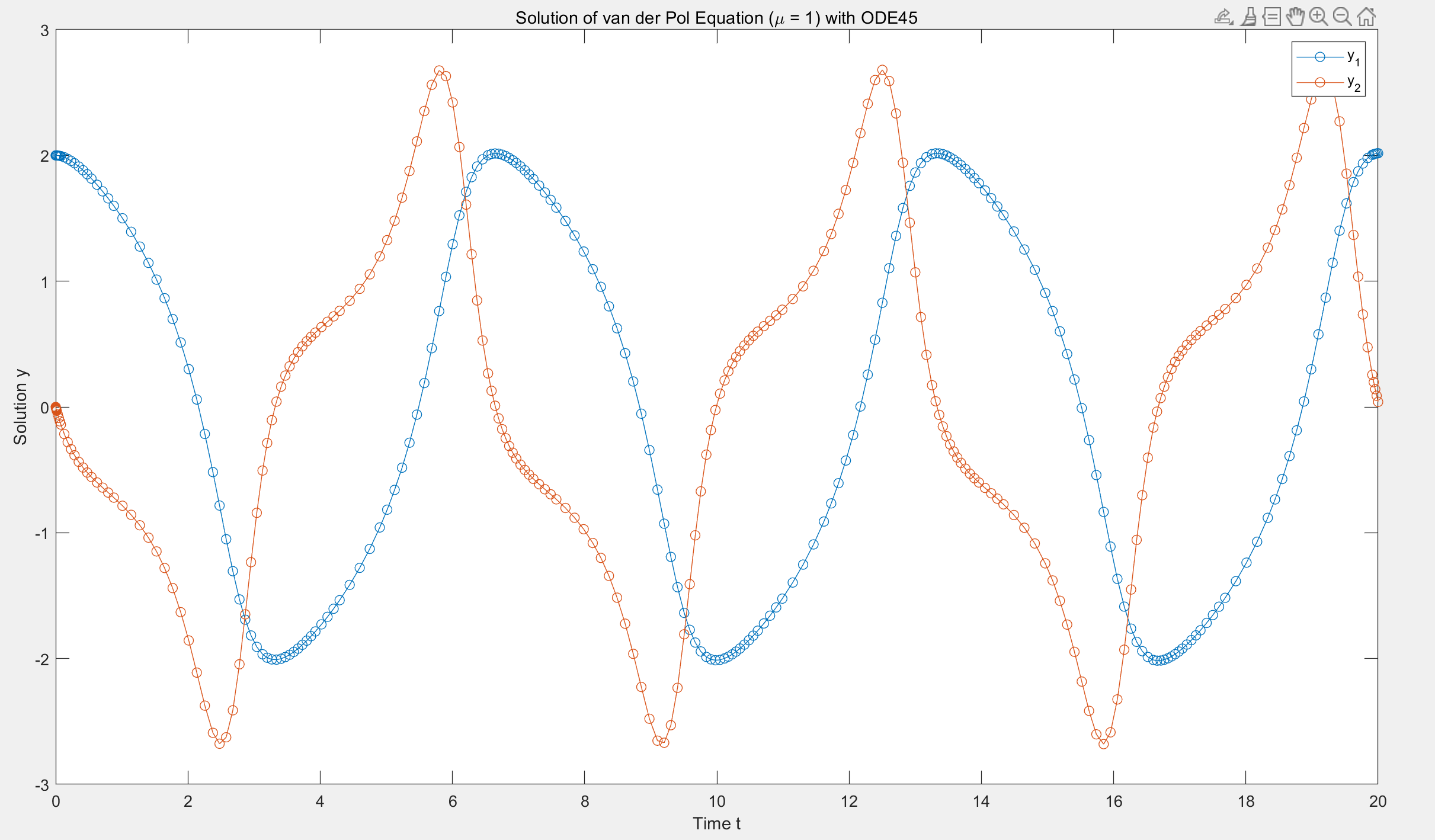
步长大概为 0.1 左右, 而且不固定, 真抽象啊 matlab

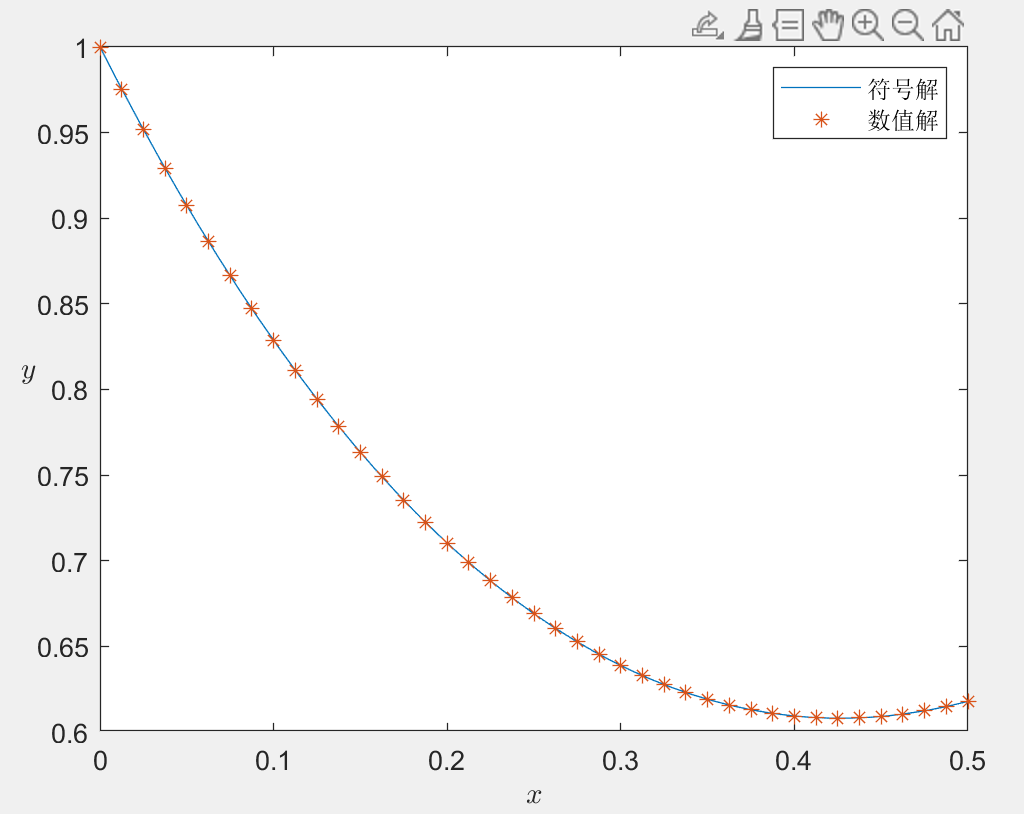
求微分方程 $y'=-2y+2x^2+2x,\;y(0)=1, 0 \leq x \leq 0.5$ 的数值解, 并在同一个界面上画出数值解和解析解的曲线

clc, clear, close all, syms y(x)
y = dsolve(diff(y) == -2*y+2*x^2+2*x, y(0)==1);
dy = @(x,y) -2*y+2*x^2+2*x;
[sx,sy] = ode45(dy,[0,0.5], 1);
fplot(y,[0,0.5]); hold on;
plot(sx,sy,'*'); legend({'符号解','数值解'})
xlabel('$x$','Interpreter','latex');
ylabel('$y$','Interpreter','latex','Rotation',0); % 不然字母 y 会旋转

人口模型

马尔萨斯人口模型

对于这个模型, 有假设:
(1) 设 x(t) 表示 t 时刻的人口数, 且 x(t) 连续可微
(2) 人口的增长率 r 是常数 (增长率=出生率-死亡率)
(3) 人口数量的变化是封闭的, 即人口数量的增加与减少只取决于人口中个体的生育和死亡, 且每一个体都具有同样的生育能力和死亡率

由假设, t 时刻到 t+Δt 时刻人口的增量为 x(t+Δt) -x(t) = rx(t)Δt, 有 dx = rx * dt, x(0) = x0,
解得 $x(t) = x_0e^{rt}$ , 显然扯淡, 于是要修正

Logistic 模型

也称阻滞增长模型在人口较少时, 可以把增长率 r 看成常数, 那么当人口增加到一定数量之后, 就应当视 r 为一个随着人口的增加而减小的量, 即将增长率 r 表示为人口 x(t) 的函数 r(x), 且 r(x) 为 x 的减函数, 有假设:
(1) 设 $r(x)$ 为 $x$ 的线性函数, $r(x) = r-sx$ (先假设为一次函数)
(2) 自然环境所能容纳的最大人口数为 $x_m$, 即当 $x=x_m$ 时, 增长率 $r(x_m) = 0$
由假设, $\displaystyle r(x) = r\left(1 - \frac{x}{x_m}\right)$ , 有
\[ \left\{\begin{aligned} &\frac{dx}{dt} = r\left(1-\frac{x}{x_m}\right)x, \\ &x(t_0) = x_0. \end{aligned}\right. \] 解为 $x(t) = \displaystyle \frac{x_m}{\displaystyle1+\left(\frac{x_m}{x_0}-1\right)e^{-r(t-t_0)}}$
这个模型有一些特点, $x(t)$ 单增, 变化率 $dx/dt$ 在 $x = \frac{x_m}{2}$ 时最大, 总体就是生物的 $S$ 型曲线
实际应用还是 Matlab - APP - Curve Fitting Tool - Logistic 拟合
或者你用 Custom Equation, 然后把算出来的 x(t) 填进去, 例如:

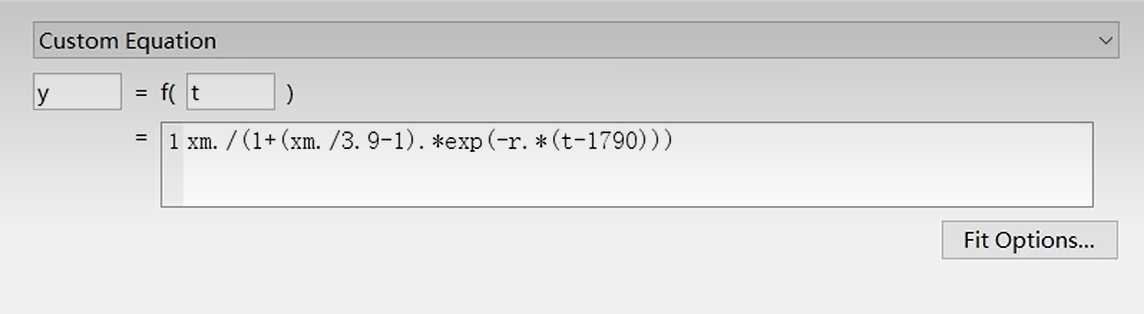
拟合的过程中能估计出来 $x_m$ 和 $r$, 得到了函数就可以拿来估计后续了

相互作用模型

种群竞争模型略
互惠共存模型略

弱肉强食模型(Lotka-Volterra模型)
此类问题广泛存在于自然界中, 如大鱼吃小鱼、狼群与羊群等
设 $t$ 时刻第一个种群的数量和第二个种群的数量分别为 $x_1(t),\; x_2(t)$ , 初始种群数量为 $x_1^0, \;x_2^0$
有一些基本假设:
(1) 第一个种群的生物捕食第二个种群的生物, 其种群数量的变化除了自身受 Logistic 规律的制约外, 还受到被捕食的第二个种群的数量影响
(2) 第二个种群的数量变化除了自身受自限规律影响外, 还受其天敌第一个种群的数量影响。第二个种群的种群数量越多, 被捕杀的机会越多, 从而第一个种群的繁殖越快
(3) 设两个种群的自然增长率分别为 $r_1$ 和 $r_2$, 各自独自生存的生存极限数分别为 $K_1$ 和 $K_2$

由假设, 有 $\displaystyle \frac{dx_1}{dt} = r_1\left(1-\frac{x_1}{K_1}\right)x_1 + b_{12}x_1x_2, \;\; \frac{dx_2}{dt} = r_2\left(1-\frac{x_2}{K_2}\right)x_2 - b_{21}x_1x_2$
其中 $b_{12}, b_{21} > 0$, 为两个种群的接触系数, 并不一定相同, 再加上初始条件 $x_1(0)=x_1^0,\;x_2(0)=x_2^0$ 就可以开解微分方程了

eg. 已知捕食者-被捕食者方程组:
\[ \left\{\begin{aligned} &\frac{dx}{dt} = 0.2x-0.005xy,\;x(0)=70, \\ &\frac{dy}{dt} = -0.5y+0.01xy,\;y(0)=40. \end{aligned}\right. \] 式中: $x(t)$ 表示 $t$ 个月后兔子的总体数量, $y(t)$ 表示 $t$ 个月后狐狸的总体数量
请研究以下问题: (1). $x(t),y(t)$ 变化的周期; (2). $x(t)$ 总体数量的最值; (3). $y(t)$ 总体数量的最值。

我们先令 $0.2x-0.005xy = -0.5y+0.01xy = 0$, 解得临界点 $(50,40)$

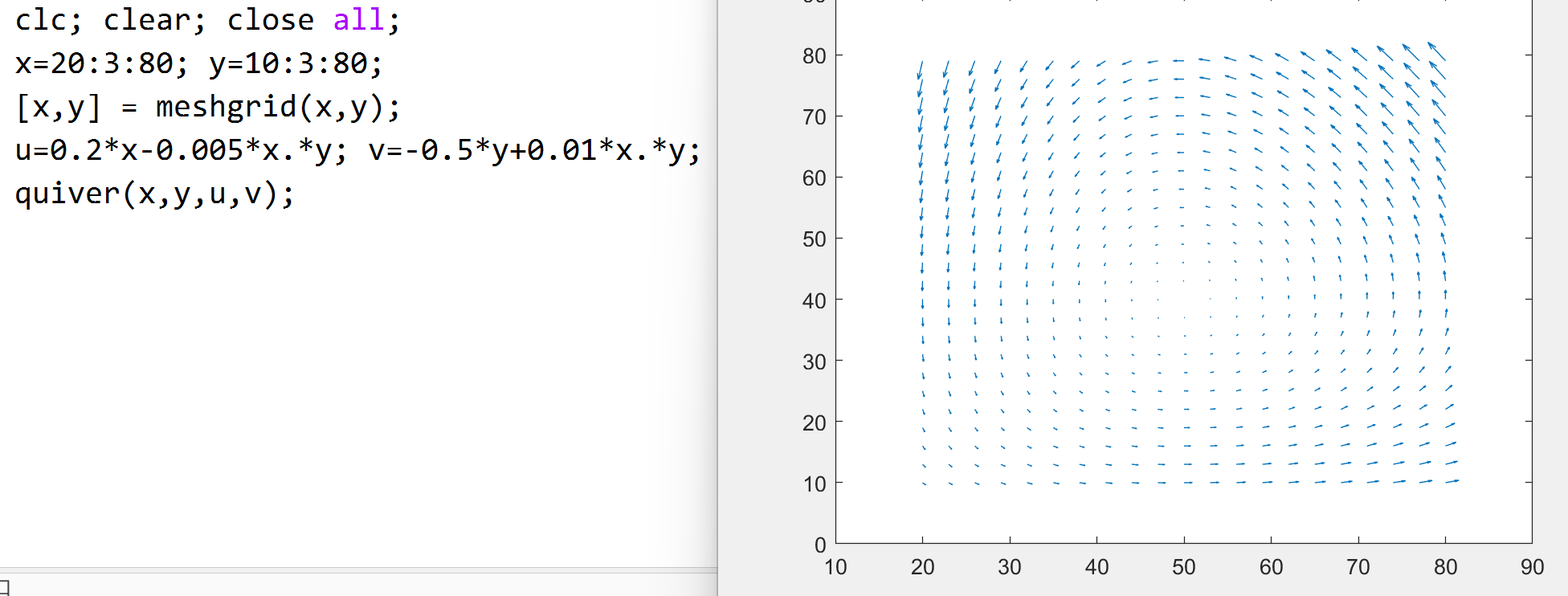上图是炫酷的向量场图象, x, y 就绕这个来变化
好像没什么用？还是画出 $x(t),\;y(t)$ 解的图象吧……
需要用到一个函数: y = deval(sol,x) 可以计算 x 中包含的点处的微分方程问题的解 sol, y = deval(___,idx) 只返回带有向量 idx 中所列索引的解分量
可能还需要一个函数:
x = fminbnd(fun,x1,x2) 返回一个值 x，该值是 fun 中描述的标量值函数在区间 x1 < x < x2 中的局部最小值
[x,fval] = fminbnd(___) 返回 x 与目标函数在 fun 的解 x 处计算出的值

clc; clear; close all; % 下文范围默认 [0,100]
dxy = @(t,z) [0.2*z(1)-0.005*z(1)*z(2); -0.5*z(2)+0.01*z(1)*z(2)];
sol = ode45(dxy,[0,100],[70;40]);
xt = @(t)deval(sol,t,1); yt = @(t)deval(sol,t,2);
hold on;
fplot(xt,[0,100],'--','LineWidth',1.5);
fplot(yt,[0,100],'LineWidth',1.5);
xlabel('$t$','Interpreter','latex');
legend({'$x(t)$','$y(t)$'},'Interpreter','latex');
[xt1,fx1] = fminbnd(xt,0,100) % 求 x 的最小点及最小值
[xt2,fx2] = fminbnd(@(t)-xt(t),0,100) % 求 x 的最大点及最大值
[yt1,fy1] = fminbnd(yt,0,20) % 求 y 在 [0,20] 上的最小点及最小值
[yt2,fy2] = fminbnd(yt,20,40) % 求 y 在 [20,40] 上的最小点及最小值
T = yt2-yt1 % 求周期 (事先画图估计过在 20 左右)
[yt3,fy3] = fminbnd(@(t)-yt(t),0,100) % 求 y 的最大点及最大值
%-----------------------------------------------
xt1, fx1 = 8.9150, 34.2513
xt2, fx2 = 60.6487, -69.8810 % 取反后实为 69.8810
yt1, fy1 = 14.9932, 21.5086
yt2, fy2 = 35.2133, 21.5644
T = 20.2201
yt3, fy3 = 64.7762, -66.7664 % 取反后实为 66.7664

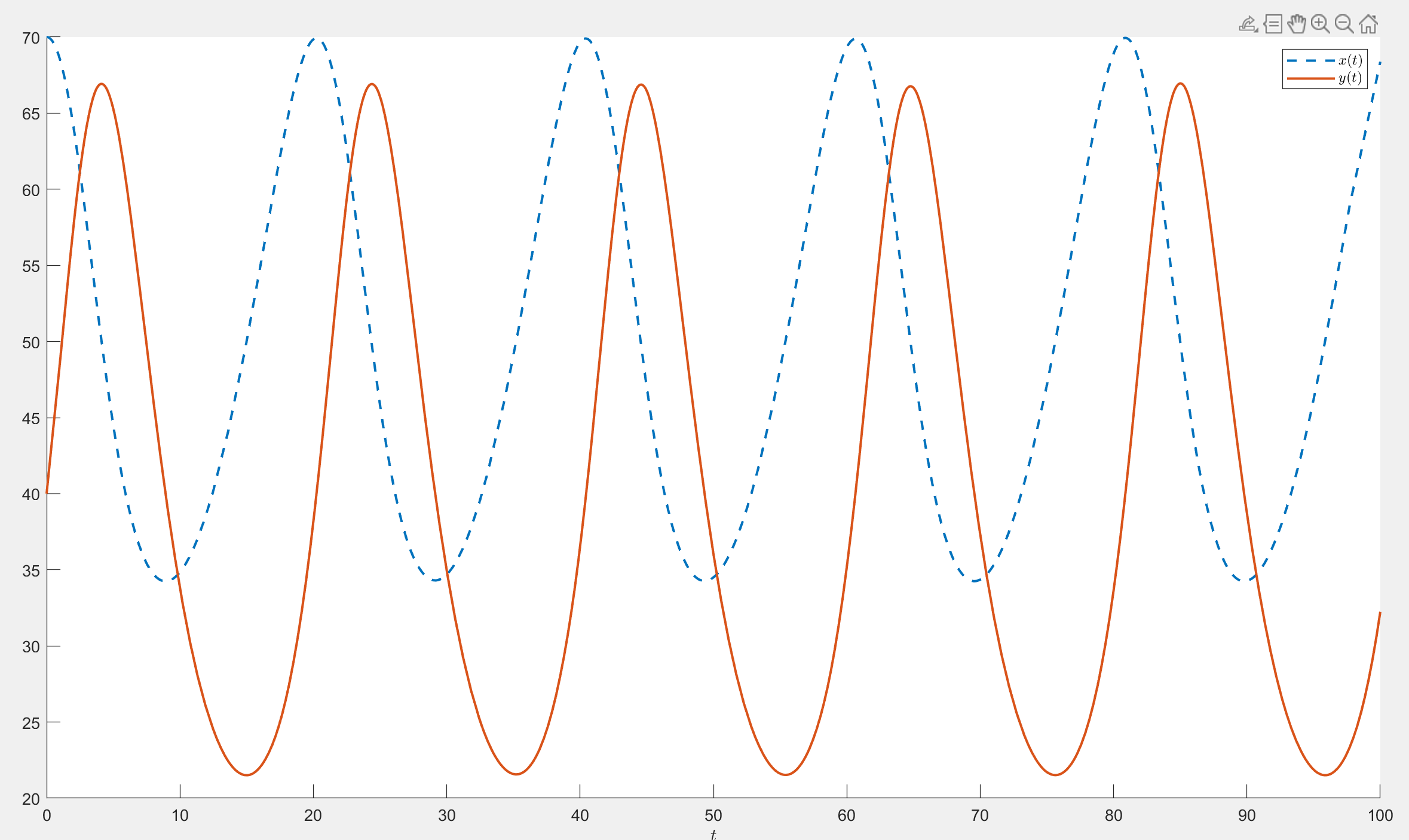
传染病模型(笔记待补)

SI 模型和 Logistic 模型一样, 略
SIS 模型进一步假设了每天被治愈的病人占总人数的比例为 $\mu$, 以及痊愈的病人还能被感染
SIR 假设:
(1) 人群分健康者、病人和病愈后因具有免疫力而退出系统的移出者三类。设任意时刻 t 这三类人群占总人口的比例分别为 $s(t), i(t)$ 和 $r(t)$
(2) 病人的日接触率为 $\lambda$, 日治愈率为 $\mu$, 传染强度 $\sigma = \lambda/\mu$
(3) 人口总数 N 为固定常数
总体方程组为:
\[ \left\{\begin{aligned} &\frac{di}{dt} = \lambda s i- \mu i,\\ &\frac{ds}{dt} = -\lambda s i, \\ &\frac{dr}{dt} = \mu i, \\ &i(0)=i_0, s(0)=s_0, r(0)=0 \end{aligned}\right. \]

K-Means 聚类算法

算法目标是将数据集划分为 K 个簇(Clusters), 最小化簇内的点到簇中心(centroid)的距离总和
主要还是调库, 核心代码就一行 [idx centroid] = kmeans(data, Clusternum)
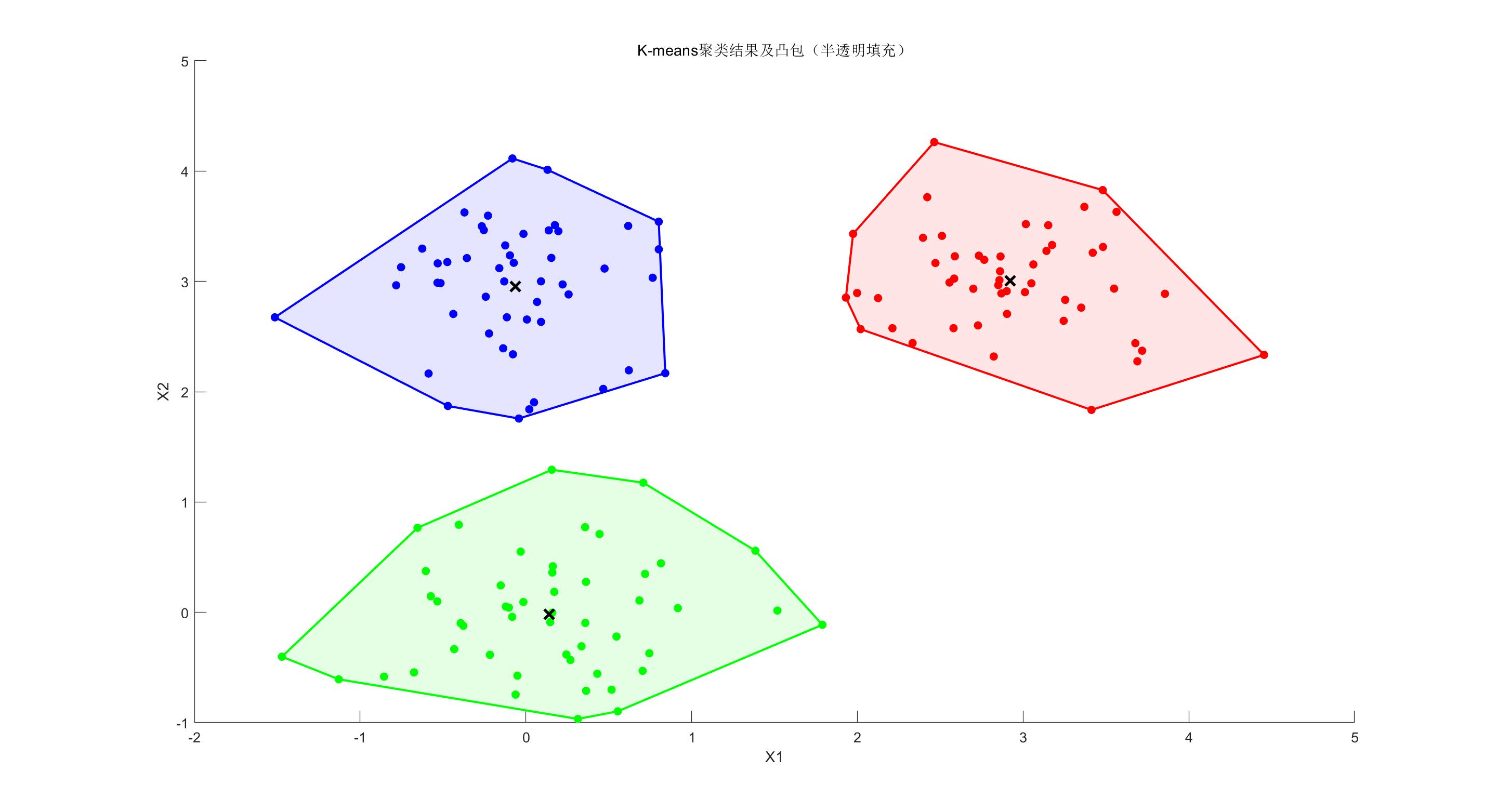
在实际绘图中为了好看你还可以画出外层凸包
二维最清晰好看, 可惜只能有两个指标

% 生成随机数据（三个簇）
rng default; % 设置随机种子保证结果可重复
data1 = randn(50, 2)*0.5 + [0, 0];
data2 = randn(50, 2)*0.5 + [3, 3];
data3 = randn(50, 2)*0.5 + [0, 3];
X = [data1; data2; data3];

% 应用K-means算法进行聚类
k = 3; % 聚类数目
[idx, centroids] = kmeans(X, k);

% 分割数据到各个聚类
clusters = cell(k, 1);
for i = 1:k
    clusters{i} = X(idx == i, :);
end

% 计算每个聚类的凸包并绘图
figure;
hold on;
colors = {'r', 'g', 'b'}; % 每个聚类的颜色

for i = 1:k
    % 当前聚类的数据
    currentCluster = clusters{i};
    % 绘制数据点
    scatter(currentCluster(:, 1), currentCluster(:, 2), [], colors{i}, 'filled');
    % 计算凸包
    hullIndices = convhull(currentCluster(:, 1), currentCluster(:, 2));
    hullPoints = currentCluster(hullIndices, :);
    % 绘制凸包边界
    plot(hullPoints(:, 1), hullPoints(:, 2), 'Color', colors{i}, 'LineWidth', 1.5);
    % 填充凸包区域，颜色半透明
    fill(hullPoints(:, 1), hullPoints(:, 2), colors{i}, ...
        'FaceAlpha', 0.1, 'EdgeColor', 'none'); % FaceAlpha 控制透明度
end

% 可选：绘制聚类中心
scatter(centroids(:, 1), centroids(:, 2), 100, 'k', 'x', 'LineWidth', 2);
title('K-means聚类结果及凸包（半透明填充）');
xlabel('X1');
ylabel('X2');

代码由 deepseek 编写, 在 legend 方面可能有点问题, 我就直接去掉了

Matlab 基础入门

http://example.com/2025/02/06/Matlab/

作者

Frankly6

发布于

2025-02-06

更新于

2025-03-28

许可协议

matlab

	L	M	N	Pa	Pe	T
L		56	35	21	51	60
M	56		21	57	78	70
N	35	21		36	68	68
Pa	21	57	36		51	61
Pe	51	78	68	51		13
T	60	70	68	61	13

	L	M	N	Pa	Pe	T
L		56	35	21	51	60
M	56		21	57	78	70
N	35	21		36	68	68
Pa	21	57	36		51	61
Pe	51	78	68	51		13
T	60	70	68	61	13

Matlab 基础入门

Matlab

矩阵

创建矩阵

矩阵元素修改

矩阵拼接

矩阵重构与重排

矩阵的运算

调用函数运算

矩阵加减

矩阵乘/除/乘方/转置

矩阵关系运算

逻辑

运算符

常用函数

语法结构

条件结构

循环结构

函数

自定义函数

匿名函数

特殊函数

常用函数

三角函数

图形绘制

二维绘图

plot 函数

fplot 函数

fimplicit 函数

其他绘图函数

图形属性设置

三维绘图

三维曲面

句柄与窗口

MCM/ICM Matlab

使用 optimproblem 创建和求解优化问题

遗传算法(Genetic Algorithm)

蒙特卡洛法

图论绘图

旅行商问题(TSP)

插值

分段线性插值

三次样条插值

pchip 分段三次插值

griddedInterpolant 函数

拟合

最小二乘法

微分方程

解析解

数值解

人口模型

马尔萨斯人口模型

Logistic 模型

相互作用模型

传染病模型(笔记待补)

K-Means 聚类算法

作者

发布于

更新于

许可协议

目录

使用 `optimproblem` 创建和求解优化问题

	L	M	N	Pa	Pe	T
L		56	35	21	51	60
M	56		21	57	78	70
N	35	21		36	68	68
Pa	21	57	36		51	61
Pe	51	78	68	51		13
T	60	70	68	61	13