CS61A 笔记

包含简单的 Python, Scheme, SQL 和编程思想的学习

中文课本链接 / 英文版
课程官网
我的 Projects 代码库

函数构建抽象

交互模式的 python: python -i xxx.py
主要是这个 -i 起作用(interact?)

定义函数:

def f(x): #f(x, y), f(), ...
    return ... #eg. "return a, b, c" then you can code "i, j, k=f(x)"
#----------OR----------
g = f

导入:

from math import pi
from operator import add, mul
from math import * #不要全导进来, 关键字太多, 不同包还可能重复

多元素赋值:

a, b = 1, 2
b, a = a+b, b  #b=3, a=2 then

当使用一个名称时，程序会在当前的环境中查找该名称绑定的值，如果没有找到，则会向外层环境继续查找，直到找到为止。(local frame -> global frame)(局部 -> 全局)

print 与 None:

>>> print(print(1), print(2))
1
2
None None

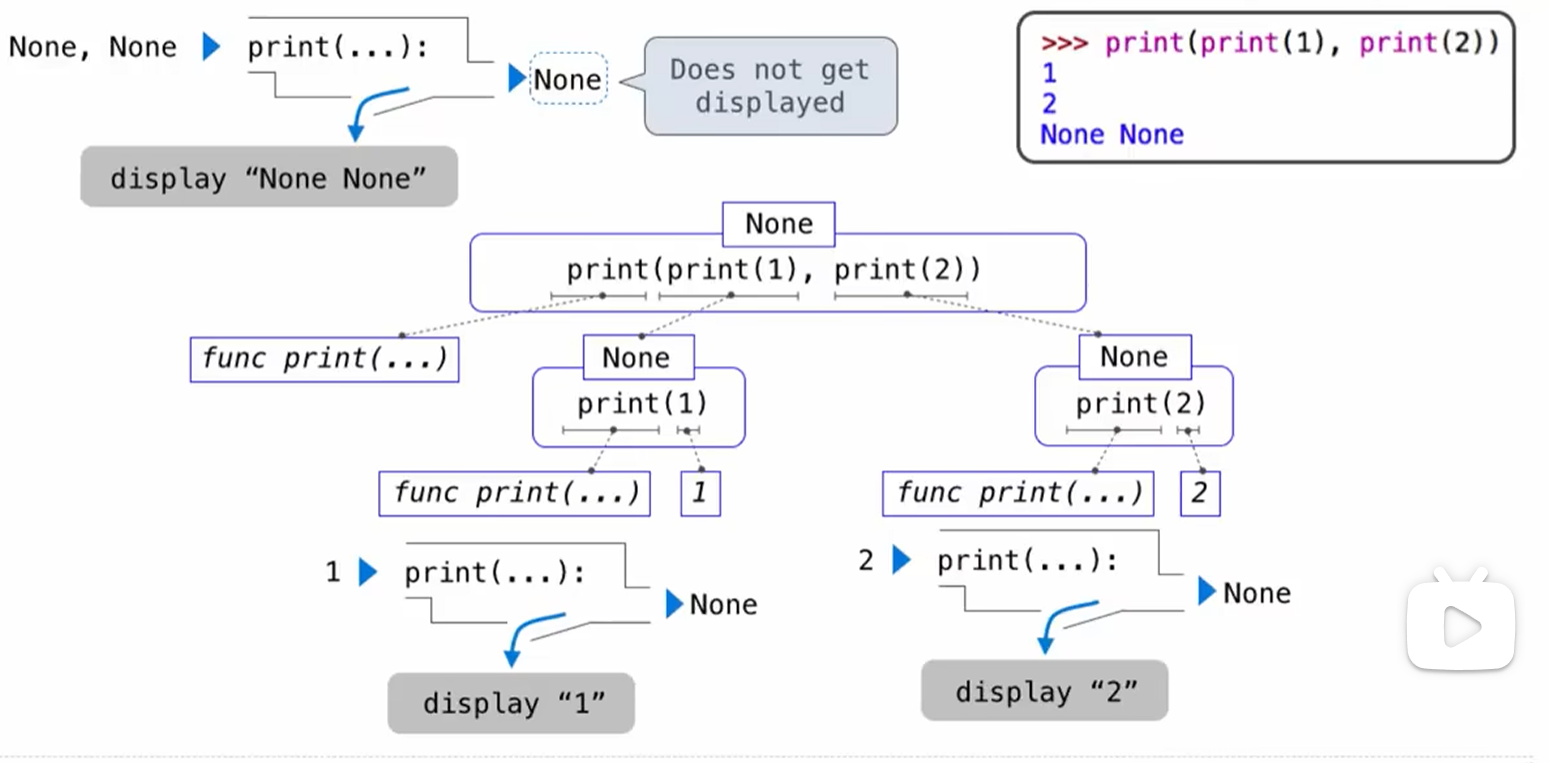print() 没有返回量, 返回 None, 最外层 print() 的 None 不会显示, 自己定义没有返回量的函数最后要 return None

整除符号 \(//\)​​ , 也可以用 operator 里的 floordiv(a, b) 替代
数的次方符号 \(**\) , 例如 \(10 ** \;1000 = 10^{1000}\)

函数传默认参(如果没有传参进来, 用默认参, 参数从左到右依次传):

def f(x, y=10): return x+y
a = f(10) #a = 20
a = f(10, 15) #a = 25

假设语句 if/elif/else (elif = else if) , 不加括号, 直接 if <condition>: ...

迭代-while语句: (下面是一个斐波那契数列的程序, 可以玩玩, 我真心希望它能加载出来)

文档测试(Doctests): 文档字符串的第一行应该包含函数的单行描述，接着是一个空行，下面可能是参数和函数意图的详细描述。此外，文档字符串可能包含调用该函数的交互式会话示例:

>>> def sum_naturals(n):
        """返回前 n 个自然数的和。
        
        >>> sum_naturals(10)
        55
        >>> sum_naturals(100)
        5050
        """
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total

然后，可以通过 doctest 模块 来验证交互，如下:

>>> from doctest import testmod
>>> testmod()
TestResults(failed=0, attempted=2)

assert语句: 与其在程序运行时崩溃, 不如在出现错误条件时就崩溃。

assert a>0, 'a 必须为正数' #在a>0时向下运行, 在a<=0时抛出崩溃信息

高阶函数: 例如在求正方形, 正六边形, 圆形的面积时, 其面积都可以表达为 \(C \times r^2\) 其中 \(C\) 是一个常数, 我们可以把这个常数在代码中定义为一个函数(同理也有 \(f(x) \times r^2\)), 这个函数可以被传入求面积的函数中, 求面积的函数就称为高阶函数。

函数内定义函数:

def make_adder(n):
    def adder(k):
        return k+n
   	return adder            #make_adder(1)(2) = 3 或者 f=make_adder(1), f(2)=3

Lambda 表达式: 其结果是一个匿名函数(Lambda 函数), 让你不用想一个函数名, 让代码简洁难懂

def make_adder(n):
    return lambda k: n + k

x = 10
square = x*x #square 是一个值, square=100
square = lambda x: x*x #square 是一个函数, square(10)=100, square(4)=16

def compose(f, g):
    return lambda x: f(g(x))
f = compose(lambda x: x*x, lambda y: y+1)
ans=f(12)   #ans=169, guess why?

def search(f):
	x=0
   	while not f(x): x+=1
    return x
def square(x): return x*x
def inverse(f): return lambda y: search(lambda x:f(x)==y)    """Return g(y) such that g(f(x)) -> x."""
#----------------------------------------------
>>> sqrt = inverse(square)
>>> sqrt(256)    #y = 256, then search(lambda x:square(x)==256) -> return 16
16

与/或(\(and/or\))运算是按顺序的, 若前面不满足条件则不会往下运算(可以被"短路")
函数调用会先检查所有传参, 所以不能(不建议)用函数来创造三目运算符
a if b else c: 如果 b 为真, 执行 a, 否则执行 c

*args:不定参数, 不知道有几个参数会发过来
f(1,2,3) = f(*[1,2,3]) , *起到了压缩/解压参数列表的作用
(不准发键值对, 否则用 **kwargs (接收 N 个关键字参数, 转换成字典 dict 形式) ):

>>> def printed(f):
...     def print_and_return(*args):
...         result = f(*args)
...         print('Result:', result)
...         return result
...     return print_and_return
>>> printed_pow = printed(pow)
>>> printed_pow(2, 8)  # *args represents the arguments (2, 8)
Result: 256
256
>>> printed_abs = printed(abs)
>>> printed_abs(-10)  # *args represents one argument (-10)
Result: 10
10

递归函数, 进行自调用:

def print_sum(x):
    print(x)
    def next_sum(y):	
        return print_sum(x+y)
   	return next_sum
print_sum(1)(3)(5)  #print_sum(1)/print_sum(1)(3)/print_sum(1)(3)(5) 都是一个next_sum函数  
#---------------------------------
1
4
9

装饰器(decorator):
装饰器本质上是一个函数，它可以接收一个函数作为参数并返回一个新的函数。这个新函数是对原函数的一种包装或增强，可以在不改变原函数代码的前提下，增加额外的功能 (eg. 在 cats 项目中给你的爆搜加个记忆化)
装饰器内部有包装函数, 装饰器在内部定义它并返回它, 使用 @ 语法, 见下例:

def trace(f): # f 即被装饰函数
    def traced(x):
        print('Calling',f,'on argument',x)
        return f(x)
    return traced

@trace
def square(x):
    return x*x
print(square(12))
#-----------------------------------
Calling <function square at 0x000001F0A104EF80> on argument 12
144

一道程序填空难题, 题面见下(禁止使用 list, set, 或其他笔记中未提及的):

def repeat(k):
    """When called repeatedly, print each repeated argument
    
    >>> f = repeat(1)(7)(7)(3)(4)(2)(5)(1)(6)(5)(1)
    7
    1
    5
    1
    """
    return ___(k)

def detector(f):
    def g(i):
        if ___:
            ___
        return ___
    return g

一种可能答案见下:

def repeat(k):
    """When called repeatedly, print each repeated argument
    
    >>> f = repeat(1)(7)(7)(3)(4)(2)(5)(1)(6)(5)(1)
    7
    1
    5
    1
    """
    return detector(lambda j: False)(k)

def detector(f): #f = have_seen_i_before
    def g(i):    #g = updated_have_seen_i_before
        if f(i):
            print(i)
        return detector(lambda j: j==i or f(j)) 
    #每一次迭代相当于添加了一个 lambda 函数在 list 中
    return g

这体现了函数构建抽象的思想, 你知道了 \(f(i)\) 的含义, 就不用想它, 直接用就是了

递归(recursion): 自我调用
迭代是递归的特殊情况, 用具体功能理解抽象函数, 在写递归时做出信仰之跃

一行的递归求阶乘算法:

def fac():
    return (lambda y: y(y))(lambda y: lambda x: 1 if x==1 else x*y(y)(x-1))
#----------------------哈哈我也看不懂----
>>> fac()(5)
120

数据构建抽象

列表(list): 类似 c++ 中的数组, 初始化 a = [a0,a1,a2,a3,...]
list 的运算, 例: a=[2,6] b=[5,8], c=a+b*2=[2,6,5,8,5,8]
新的运算符 in: 设 a=[2,6] , 此时 2 in a 为 True
高维 list: p=[[10,20], [30,40]] , 此时 p[1]=[30,40]
二维list创建: p=[[] for _ in range(M)], 创建一个 M 行的空 list, 加东西用 p[i].append(...)
注意！不建议 list 赋值时用 list_a = list_b , 在python中 list_a 相当于 list_b 的指针, 修改 list_a 会改变 list_b

list 是一种容器(container), 容器是包含其它数据类型的一种数据结构或数据类型

For循环: for <name> in <expression>: <suite>
以找在 list 中一个数出现的次数为例:

def count(s, val):
    tot=0
    for element in s:
        if element==val: tot+=1
    return tot
#------------------------------
>>> count([1,2,1,2,1],1)
3

这里的 in 有点像 c++ 的 auto 了......
对于 p[[1,2], [3,4], [2,2], [5,7]], 还可以写 for x, y in p: 这下直接步入 c++17 了
对于 a[1,2,3], a[1:]=a[1:3]=[2,3], 这里的 1: 代表从下标为 1 的元素到最后一个元素
同理有 a[:1]=a[0:1]=[1], 右边界不含

range(1,N) 可以帮助遍历 [1,N) 之间的整数, range(N) = range(0,N)

join(): 连接字符串数组。将字符串、元组、列表中的元素以指定的字符(分隔符)连接生成一个新的字符串
语法 'sep'.join(seq) , 其中 sep 为分隔符(可以为空('')), seq 为要连接的元素序列、字符串、元组、字典
返回一个以分隔符 sep 连接各个元素后生成的字符串

#eg. 将长整数每一位分割进 list 后再合并
num = input()
s = [int(d) for d in str(num)]
num = int(''.join(str(i) for i in s))

list comprehension: 一种具体/抽象构建 list 的方法, 见下例:

>>> odds=[1,3,5,7,9]
>>> [x+1 for x in odds]
[2,4,6,8,10]
>>> [x for x in odds if 25%x==0]
[1,5]

字符串(string):可用 单引号/双引号/三引号(多行常用) 定义, len(s) 求 s 的长度
string 可以直接找子串, list 不行

抽象屏障: 不要直接玩弄抽象下标了, 没人知道那代表什么, 评价为学 OI 学的, 下图是一个经典反例

这样写不利于维护和更改

字典(dictionary): 一个 key 对应一个 value, list 或 dictionary 不能被用来做 key (因为 list 是可变的, 只能用 tuple)
字典是无序的, key 是唯一对应的, 非要让 key 对应多个 value 的话, value 就用 list 吧
字典定义用大括号 {}
字典添加/修改直接写 dict["xxx"]=yyy, 或调用 update 方法 dict.update({"xxx",yyy})

numerals = {'I':1, 'V':5, 'X':10}
---------------
>>> numerals['X']
10
>>> numerals.keys()
dict_keys(['X', 'V', 'I'])
>>> numerals.items()
dict_items([('X',10), ('V',5), ('I',1)]) 
>>> 'X' in numerals
True

元组(tuple): 与 list 不同, 元组是有序且不可修改的集合, 用小括号 () 创建
元组内下标可以为负数, 你可以认为元组是无限循环的, p[-1] 可指向元组的最后一个元素
可以通过 tuple(...) 函数直接将 list 转化为元组

max函数: max(iterable[, key=func]) -> value 或 max(a, b, c, ...[, key=func]) -> value
中括号括起来的参量可以空着不写

>>> max(range(5))
4
>>> max(range(10), key=lambda x: 7-(x-4)*(x-2)) #key 相当于一个 compare 函数
3

树结构: 一个树有一个根标签(root label)和一系列分支(branch)。树的每个分支都是一棵树, 没有分支的树称为叶子(leaf)。树中包含的任何树都称为该树的子树(例如分支的分支)。树的每个子树的根称为该树中的一个节点(node)。 python 的 list 套 list 结构可以帮助我们很快构建一颗树:

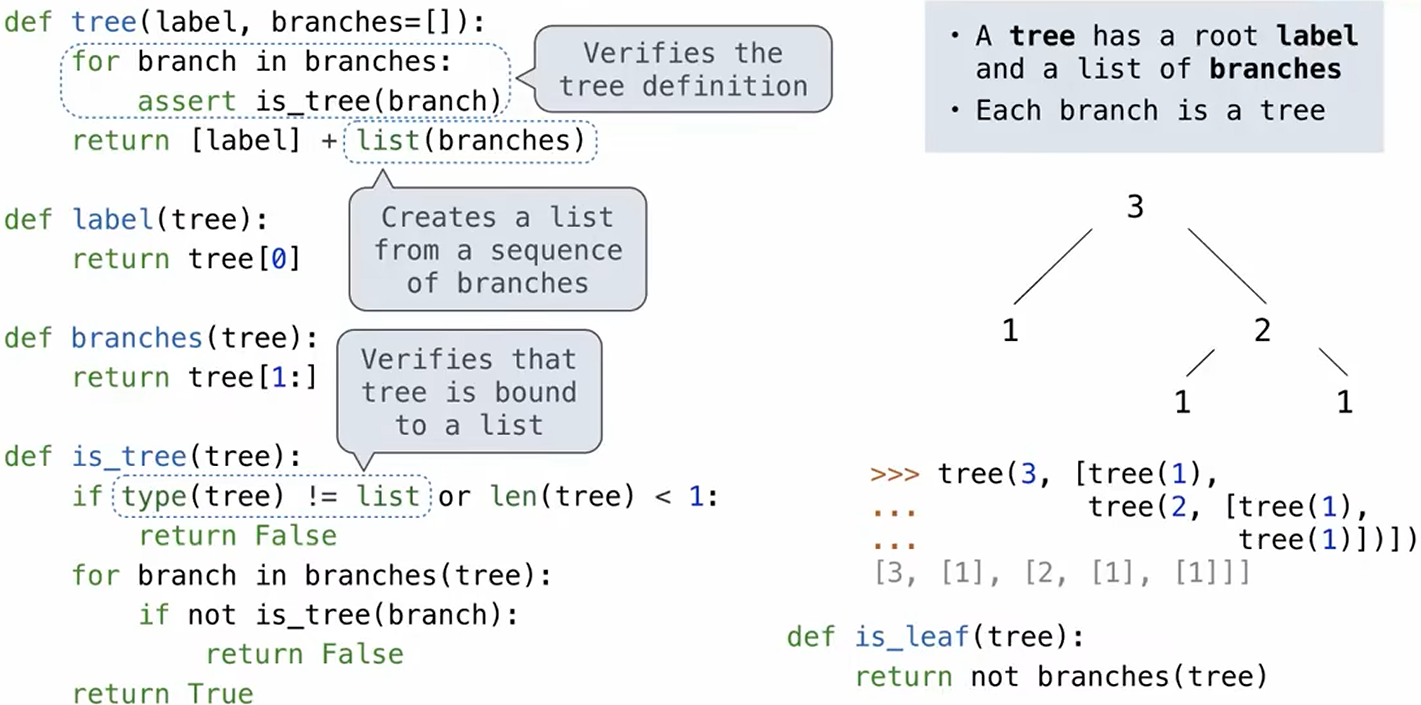
下图为斐波那契树的构造:

def fib_tree(n):
    if n<=1: return tree(n)
	else:
        left, right = fib_tree(n-2), fib_tree(n-1)
        return tree(label(left)+label(right),[left, right])
-----------------------------------------
>>> fib_tree(4)
[3, [1, [0], [1]], [2, [1], [1, [0], [1]]]]

list 及 子list 的第一项都是树及子树的根
这样建树太抽象了, 我还是用我的 append 吧……

all(): 接收一个 list , 全真为真, 其余为假
any(): 接受一个 list , 全假为假, 其余为真
zip(): 将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表

>>> a = [1,2,3]
>>> b = [4,5,6]
>>> c = [4,5,6,7,8]
>>> zipped = zip(a,b)     # 打包为元组的列表
[(1, 4), (2, 5), (3, 6)]
>>> zip(a,c)              # 元素个数与最短的列表一致
[(1, 4), (2, 5), (3, 6)]
>>> zip(*zipped)          # 与 zip 相反，*zipped 可理解为解压, 返回二维矩阵式, 每个元组长度相同
[(1, 2, 3), (4, 5, 6)]	  # == zip(s*zip(a,b)) / list(tuple(a),tuple(b))

一些没用二进制知识的回忆:
原码: 原码是最直观的表示方法, 它直接用二进制数表示一个数, 包括正负号。在原码中, 最高位(最左边的位)是符号位, 0 表示正数, 1 表示负数, 其余位表示数值本身。例如, 十进制数 +5 的原码表示为 0000 0101, 而 -5 的原码表示为 1000 0101。
反码: 反码主要用于表示负数。对于正数, 其反码与其原码相同。对于负数, 其反码是将原码除符号位外的所有位取反(0 变 1, 1 变 0)。例如, 十进制数 -5 的反码表示为 1111 1010。
补码: 补码是计算机中最常用的表示方法, 用于进行二进制加法运算。对于正数, 其补码与其原码相同。对于负数, 其补码是其反码加 1。补码的一个重要特性是, 任何数的补码加上该数本身, 结果总是 0。例如, 十进制数 -5 的补码表示为 1111 1011。

这些抽象东西在做正数与负数的加法上很有用, 以 -3 + 2 为例:
2 的补码为其本身: 0000 0010
-3 的补码为: 1111 1101
两者相加所得补码: 1111 1111
此时补码为负，除符号位取反加1得到原码：1000 0001，即 -1

补码存在的本质大抵是一种模运算, 让负数与对应的正数在 \(2^n\) 上同余以此做加减

面向对象编程 (object-oriented programming) 的核心就是向数据添加状态
Python 中所有的值都是对象。也就是说，所有的值都有行为和属性，它们拥有它们所代表的数据的行为

Python 的 ord() 函数用于返回单个字符的 ASCII 数值或 Unicode 数值, 相反的, 函数 chr() 用一个范围在ASCII/Unicode 内的整数作参数，返回一个对应的字符。

# list 就是一个可变变量, python 提供了很多函数操作它
>>> chinese = ['coin', 'string', 'myriad']  # 一组字符串列表
>>> suits = chinese                         
# 为同一个列表指定了两个不同的变量名, 类似 C++ 中的 &suits = chinese 
>>> suits.pop()             		 # 从列表中移除并返回最后一个元素
'myriad'
>>> suits.remove('string')  	     # 从列表中移除第一个与参数相同的元素
>>> suits.append('cup')              # 在列表最后插入一个元素
>>> suits.extend(['sword', 'club'])  # 将另外一个列表中的所有元素添加到当前列表最后
>>> suits[2] = 'spade'  			 # 替换某个元素
>>> suits
['coin', 'cup', 'spade', 'club']
>>> suits[0:2] = ['heart', 'diamond']  # 替换一组数据
>>> suits
['heart', 'diamond', 'spade', 'club']
>>> chinese  # 这个变量名与 "suits" 指向的是同一个列表对象
['heart', 'diamond', 'spade', 'club']

#append 与 extend 与 s=s1+s2 是复制后传参
#如果你要写类似于 s=[s1]+[s2] 这样的东西, 注意此处的s1, s2为实参！

因为传实参的一些特性，你可以玩抽象的递归 list:

t = [1,2,3]
t[1:3]=[t]
t.extend(t)
print(t)
>>> [1, [...], 1, [...]]

因为 python 默认取地址的特性, 我们想复制一份不关联的形参可能要这么写:

nest = list(suits)  # 复制一个与 suits 相同的列表，并命名为 nest

你可以用 is 运算符看两个名称是否为同一个变量:

a = [10]
b = a
c = [10] ## a==b==c
>>> a is b
True
>>> a is c
False

tuple (用小括号 () 创建)是不可变的，但如果元组中的元素本身是可变数据，那我们也是可以对该元素进行操作的:

nest = (10, 20, [30, 40])
nest[2].pop() #合法
nest[2] = 30 #不合法

python 函数的默认值很危险, 因为它默认是 static 的！

python 的函数好像也默认传的实参:

def f(s):
    s.pop()
four = [1,2,3,4] #len(four)=4
f(four) #len(four)=3

python 的函数也可以是有状态的, 相同的输入可能产生不同的结果
多次调用同一个函数得到的结果却不相同，副作用之所以会出现，是因为函数更改了它所在的栈帧之外的变量
下面以一个取钱函数为例:

def make_withdraw(balance):
    """返回一个每次调用都会减少 balance 的 withdraw 函数"""
    def withdraw(amount):
        nonlocal balance                 # 声明 balance 是非局部的
        if amount > balance:
            return '余额不足'
        balance = balance - amount       # 重新绑定
        return balance
    return withdraw
withdraw = make_withdraw(100)
# 如果注释掉 nonlocal balance, 那么 python 在编译时会认为 balance 绑定的是 local frame, 而程序在声明前就调用了它

这里的 nonlocal 是一种非局部声明, 当 balance 属性为声明为 nonlocal 后, 每当它的值发生更改时, 相应的变化都会同步更新到 balance 属性第一次被声明的位置, 如果在声明 nonlocal 之前 balance 还没有赋值, 则 nonlocal 声明将会报错。
其实一般不用这东西，你重新绑一个名字 eg. b=[balance] 就行了

iterator 迭代器
迭代器是可以迭代的对象，这意味着你可以遍历所有值

s = [[1,2],3,4,5]
t = iter(s)
next(t)
>>> [1,2]
next(t)
>>> 3

在字典中迭代顺序是插入顺序, 可以选择迭代 .keys()/.values()/.items()
在 for 循环中遍历 list 的迭代器，只能 for 一次, 第二次因为迭代器到达了末尾而无法进行

map(function, iterable, ...) 会根据提供的函数对指定序列做映射
第一个参数 function 以参数序列中的每一个元素调用 function 函数, 返回包含每次 function 函数返回值的新列表

>>> map(lambda x:x^2, [1,3,5,7,9])
[1,9,25,49,81]

filter(function, iterable) 函数用于过滤序列，过滤掉不符合条件的元素, 返回由符合条件元素组成的新列表
该函数接收两个参数, 第一个为函数, 第二个为序列, 序列的每个元素作为参数传递给函数进行判断, 然后返回 True 或 False, 最后将返回 True 的元素放到新列表中

>>> filter(lambda x:x%2==1, [1,2,3,4,5,6])
[1,3,5]

有的时候, python 的函数不会立即计算答案, 而是返回一个迭代器, 用到的时候再计算, 在一些情形下可能会出错

在 Python 中，使用了 yield 关键字的函数被称为生成器(generator), 其为一种特殊的迭代器
当在生成器函数中使用 yield 语句时, 函数的执行将会暂停, 并将 yield 后面的表达式作为当前迭代的值返回
然后, 每次调用生成器的 next() 方法或使用 for 循环进行迭代时, 函数会从上次暂停的地方继续执行, 直到再次遇到 yield 语句。这样, 生成器函数可以逐步产生值, 返回多次, 而普通函数只返回一次结果

def countdown(n):
    while n > 0:
        yield n
        n -= 1
gen = countdown(5) 
print(next(gen))  # 输出: 5
print(next(gen))  # 输出: 4
print(next(gen))  # 输出: 3 
# 使用 for 循环迭代生成器
for value in gen:
    print(value)  # 输出: 2 1

# 一个小例题: 返回给定序列的全排列, 要求用 yield 一个一个传
# eg: sorted(permutations((1, 2, 3))) = [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
# eg: sorted(permutations("ab")) = [['a','b'],['b','a']]
def permutations(seq):
   	if not seq: yield []
    else:
        for perm in permutations(seq[1:]):
            for i in range(len(seq)):
                yield perm[:i] + [seq[0]] + perm[i:]
#————————————————OR————————————————
def permutations(seq):
    if not seq: yield []
    else:
        for i in range(len(seq)):
            for arr in permutations(seq[:i]+seq[i+1:]):
                yield [seq[i]] + arr

你还可以用 yield from 一次性把可迭代对象的东西全 yield 出来

类与对象(Class & Objects)
类就像一个模板，对象是按照模板（类）生成的实例
class 语句可以创建自定义类
Python 中有一个特殊的名称 __init__ (“init”的每一侧都有两个下划线), 称为类的构造函数(constructor)
Python 类中的每个函数必须有一个额外的第一个参数名称, 按照惯例它的名称是 self, 相当于 C++ 的 *this
类属性在给定类的所有对象之间共享, 类属性的赋值会改变类的所有实例的属性值
类属性由 class 语句套件中的赋值语句创建，位于任何方法定义之外

class Account:
    interest = 0.02 #类属性
    def __init__(self, account_holder):
        self.balance = 0
        self.holder = account_holder
    def deposit(self, amount):
        self.balance += amount
        return self.balance
    def withdraw(self, amount):
        if amount > self.balance:
            return 'Insufficient funds'
        self.balance = self.balance - amount
        return self.balance
>>> a = Account("Stanley")
>>> a.balance
0
>>> a.holder
Stanley
>>> a.deposit(100)
100
>>> Account.interest = 0.05
>>> a.interest #注意, 若之前单独改变 a.interest = c, 则会输出 c 而不是 0.05
0.05

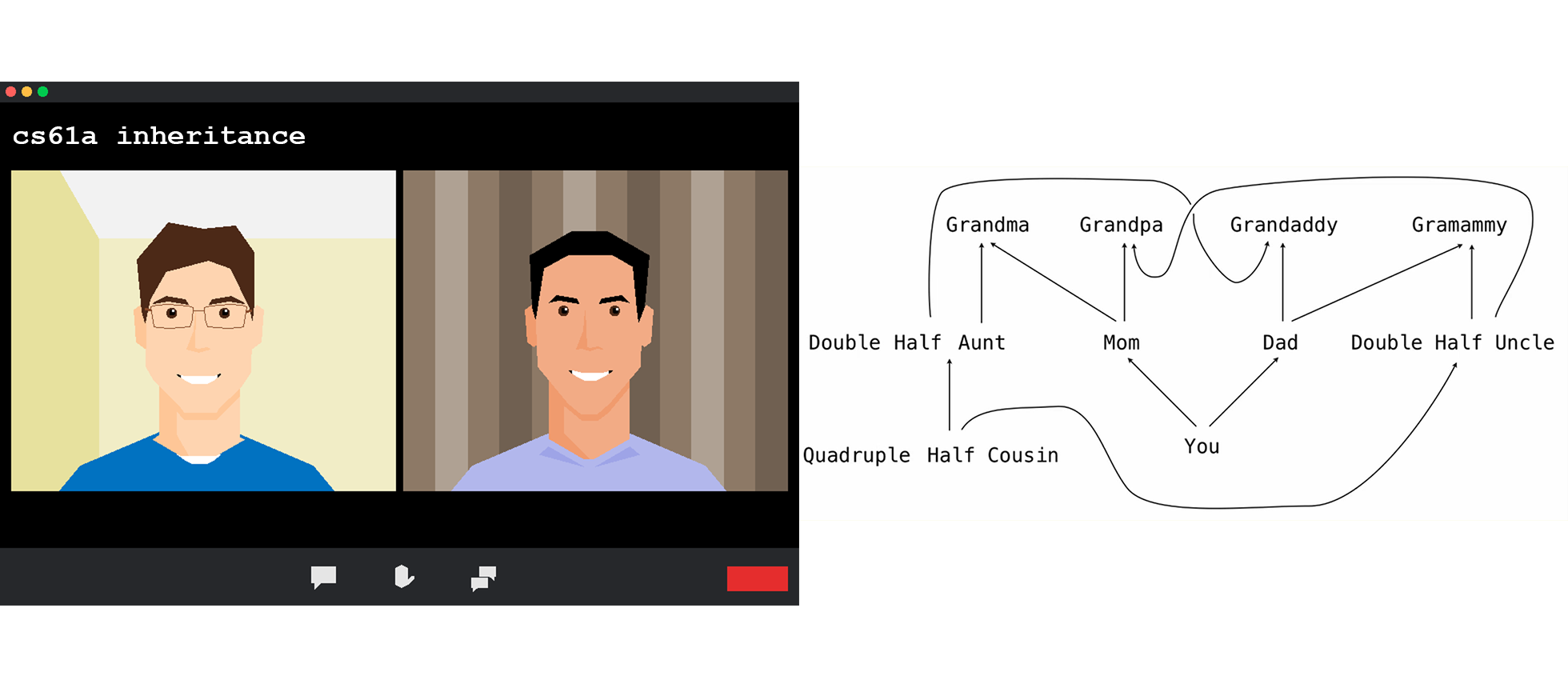
类的继承(inheritance)

#eg. 创造继承于 Account 的 CheckingAccount 类, 其会收取固定手续费, 并且利率不同
class CheckingAccount(Account): # 继承于 Account
    withdraw_fee = 1
    interest = 0.01
    def withdraw(self, amount): # 新的 withdraw 会覆盖基类的 withdraw
    	return Account.withdraw(self, amount + self.withdraw_charge)
# 不用写 __init__(), 因为基类写过了

在类中查找名称时先找当前类再找父类(基类)
我们可以用 super() 来使用父类的函数, 比如说 super().withdraw()
我们还可以写多继承, 例如 class A(B, C, D): 但是继承的排序总是令人恼火的, 我们可以通过 A.mro() 获取顺序

有时候你需要的不是继承(inheritance), 而是组合(composition), 例如下文的 Bank 类:

class Bank:
    """A bank *has* accounts
    
    >>> bank = Bank()
    >>> John = bank.open_account('John',10)
    >>> Jack = bank.open_account('Jack',5,CheckingAccount)
    >>> John.interest
    0.02
    >>> Jack.interest
    0.01
    >>> bank.pay_interest()
    >>> John.balance
    10.2
    """
    def __init__(self):
        self.accounts = []
   	def open_account(self, holder, amount, kind=Account):
        account = kind(holder)
        account.deposit(amount)
        self.accounts.append(account)
        return account
    def pay_interest(self):
        for a in self.accounts:
            a.deposit(a.balance * a.interest)

Python 规定所有的对象都应该生成两个不同的字符串表示: 一种是人类可读的文本, 另一种是 Python 可解释的表示式。字符串的构造函数, 即 str, 返回一个人类可读的字符串。如果可能, repr 函数返回一个 Python 可解释的表达式, 该表达式的求值结果一般与原对象相同

专用方法:
例如: __bool__ 方法可以用来覆盖默认真值的行为, 假设我们想让一个只有 0 存款的账号为假值。我们可以为 Account 添加一个 __bool__ 方法来实现这种行为:

Account.__bool__ = lambda self: self.balance != 0

len() 函数调用 __len__ 方法来确定其长度, 我们也可以直接调用, 有: 'Go'.__len__() = 2
__call__ 方法可以让我们定义一个行为像高阶函数的类:

>>> class Adder(object):
        def __init__(self, n):
            self.n = n
        def __call__(self, k):
            return self.n + k
>>> add_three_obj = Adder(3)
>>> add_three_obj(4)
7

自己定义这些方法就相当于重载运算符, 例如 + 的方法是 __add__, print 使用方法是 __str__ :

class Point:
    def __init__(self, x = 0, y = 0):
        self.x, self.y = x, y
    def __str__(self):
        return "({0},{1})".format(self.x,self.y)
    def __add__(self,other):
        x = self.x + other.x
        y = self.y + other.y
        return Point(x,y)
------------------------------------------------
>>> p1 = Point(2,3)
>>> p2 = Point(-1,2)
>>> print(p1 + p2)
(1,5)

这样我们就重载了 Point 类, 注意这里只重载了左加, 右加 __radd__ 可以通过 __radd__ = __add__ 来重载

链表类(linked list)

#isinstance() 函数用于判断一个对象是否是一个已知的类型, 会认为子类是父类的一个实例
class Link:
    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest
#--------------------------------------------------
>>> s = Link(3, Link(4, Link(5)))
>>> s.first
3
>>> s.rest
Link(4, Link(5))
#当然你也可以测试一些花活, 例如 s.rest.rest = s 来造循环列表

树(Tree)的类实现:

class Tree:
    def __init__(self, label, branches=[]):
        self.label = label
        for branch in branches:
            assert isinstance(branch,Tree)
        self.branches = list(branches)
    def __str__(self):
        return '\n'.join(self.indented())
    def indented(self):
        lines = []
        for b in self.branches:
            for line in b.indented():
                lines.append('  ' + line)
        return [str(self.label)] + lines
#----------------------------------
>>> t = Tree(1, [Tree(3), Tree(4)])
>>> print(t)
1
  3
  4

程序的效率问题: 比如说求个斐波那契数列, 你可以用高阶函数写记忆化, eg.

def memo(f):
    cache = {}
    def memorized(n):
        if n not in cache:
            cache[n] = f(n)
        return cache[n]
    return memorized

然后让 fib = memo(fib) 来记忆化
或者你也可以写一个装饰器

集合(set)
集合(set)是一个无序的不重复元素序列。
集合中的元素不会重复，并且可以进行交集、并集、差集等常见的集合操作。
可以使用大括号 { } 创建集合，元素之间用逗号 , 分隔， 或者也可以使用 set() 函数创建集合。

set1 = {1, 2, 3, 4}            # 直接使用大括号创建集合
set2 = set([4, 5, 6, 7])      # 使用 set() 函数从列表创建集合

>>> basket = {'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}
>>> print(basket)                      # 这里演示的是去重功能
{'orange', 'banana', 'pear', 'apple'}
>>> 'orange' in basket                 # 快速判断元素是否在集合内
True
>>> 'crabgrass' in basket
False

>>> a = set('abracadabra') # 下面展示两个集合间的运算
>>> b = set('alacazam')
>>> a                                  
{'a', 'r', 'b', 'c', 'd'}
>>> a - b                              # 集合a中包含而集合b中不包含的元素
{'r', 'd', 'b'}
>>> a | b                              # 集合a或b中包含的所有元素
{'a', 'c', 'r', 'd', 'b', 'm', 'z', 'l'}
>>> a & b                              # 集合a和b中都包含了的元素
{'a', 'c'}
>>> a ^ b                              # 不同时包含于a和b的元素
{'r', 'd', 'b', 'm', 'z', 'l'}

添加: s.add(x) 或 s.update(x)
删除: s.remove(x) 或 s.discard(x) 其中 discard 为安全删除, 如果元素不存在, 不会发生错误

计算机程序的解释

在了解函数与数据后, 我们讨论一下程序本身, python 程序是文本的集合, 而解释器决定了编程语言中表达式的含义, 但它只是另一个程序, 这一部分主要要求你写一个 Python 语言的 Scheme 解释器
我们来学习另一门程序语言 Scheme, 你可以在 61A Code 中编写并运行 Scheme 程序
你可以在 Scheme入门教程 速通一下 Scheme

Scheme 是 Lisp 的一个变种, 而 Lisp 是继 Fortran 之后仍然广受欢迎的第二古老的编程语言。
Scheme 程序主要是由各种表达式构成的, 这些表达式可以是函数调用或一些特殊的结构。一个函数调用通常由一个操作符和其后面跟随的零个或多个操作数组成, 这点和 Python 是相似的。不过在 Scheme 中, 这些操作符和操作数都被放在一对括号里：

(quotient 10 2) ; <=> (/ 10 2) <=> 5
; quotient 是整除, / 是除
; (remainder a b) 返回 a%b 的值

Scheme 的语法一直采用前缀形式。也就是说, 操作符像 + 和 * 都放在前面。函数调用可以互相嵌套, 并且可能会写在多行上:

(+ (* 3 5) (- 10 6)) ;ans = 19 (15 + 4 = 19)
(* 1 2 3 4) ;ans = 24

判断也是前缀的, 回复 #t 为 true, #f 为 false

(>= 2 1)
#t

if 表达式结构如下, 为真返回 <consequent>, 否则返回 <alternative>:

(if <predicate> <consequent> <alternative>)

and / or 格式: (and <e1> ... <en>) , (or <e1> ... <en>)
定义值:

;(define <symbol> <expression>)
> (define pi 3.14)
> (* pi 2)
6.28

定义函数(函数在 Scheme 中称为过程):

;(define (<name> <formal parameters>) <body>)
> (define (f x) (* x x))
> (f 2)
4
> (define (abs x)
    (if (< x 0)
        (-x)
        x))
> (abs -3)
3

匿名函数是通过 lambda 特殊形式创建的。Lambda 用于创建过程, 与 define 相似, 但不需要为过程指定名称, 格式为: (lambda (<formal-parameters>) <body>)
以下两种定义方式等效:

(define (plus4 x) (+ x 4))
(define plus4 (lambda (x) (+ x 4)))

Scheme 支持与 Python 相同的词法作用域规则, 允许进行局部定义。
下面, 我们使用嵌套定义和递归定义了一个用于计算平方根的迭代过程:

(define (square x) (* x x))
(define (average x y)
  (/ (+ x y) 2))
(define (sqrt x)
  (define (good-enough? guess)
    (< (abs (- (square guess) x)) 0.001))
  (define (improve guess)
    (average guess (/ x guess)))
  (define (sqrt-iter guess)
    (if (good-enough? guess)
        guess
        (sqrt-iter (improve guess))))
  (sqrt-iter 1.0))
(sqrt 9)

3.00009155413138

复合类型介绍

cond 相当于 if-elif-...-elif-else 结构:

(cond ((> x 10) (print 'big))
      ((> x 5) (print 'medium))
      (else (print 'small)))
; 你也可以这么写
(print
    (cond ((> x 10) 'big)
          ((> x 5) 'medium)
          (else 'small)))

begin 函数将多个表达式并在一起, 如 (begin (display"Hello, World!") (newline)) 会输出 Hello, world! 并回车换行

let 函数像一个局部的 define , 用完即扔

scheme 也有类似于 python 的 list, 但是这个 list 更像链表(linked list)
有一些关键词, 例如 cons car cdr nil , 我直接放一下课程截图吧......

eg. (cons (cons 4 (cons 3 nil)) s) = ((4 3) 1 2)
你也可以直接 (list list(4 3) 1 2) 来构造 list

下面是一个嵌套 list 的结构:

在 Scheme 中, 我们通过在 a b 前面加上一个单引号来引用符号 a 和 b 而不是它们的值, 见下例:

> (define a 1)
> (define b 2)
> (list a b)
(1 2)
> (list 'a 'b)
(a b)
> (list 'a b)
(a 2)

在 Scheme 中, 任何不被求值的表达式都被称为被引用。在语言中, 引号允许我们讨论语言本身, 而在 Scheme 中也是如此, 引用可以在定义之前进行

Scheme 程序语句也可以是 Scheme list, eval 函数又能将 list 解耦为程序语句:

> (list 'quotient 10 2)
(quotient 10 2)
> (eval (list 'quotient 10 2))
5

` 符号(左单引号) 代表部分引用(quasiquotation), 被部分引用的部分可以通过 ,(逗号) 解引用, 例:

> (define b 4)
> `(a ,(+ b 1))
(a 5)

下面给出 homework 08 的四个例题及代码, 有助于你理解这门没有循环, 全靠递归的语言:

; 询问 list s 是否为不降序列
(define (ascending? s) 
    (cond 
        ((or (equal? s nil) (equal? (cdr s) nil)) #t)
        ((> (car s) (car (cdr s))) #f)
        (else (ascending? (cdr s)))
    )
)
; 询问 list s 经历 pred 函数 “过滤” 后的序列
; eg. (my-filter even? '(1 2 3 4 5)) = (2 4)
(define (my-filter pred s) 
    (cond
        ((equal? s nil) nil)
        ((equal? (pred (car s)) #f) (my-filter pred (cdr s)))
        (else (append (list (car s)) (my-filter pred (cdr s))))
    )
)
; 将 lst1, lst2 两个序列互相穿插, lst1 先开始, 一个序列空后将另一个直接接在最后面
; eg. (interleave '(1 2 3) '(4 5 6)) = (1 4 2 5 3 6)
; eg. (interleave '(7 8 9 10) '(11 12)) = (7 11 8 12 9 10)
(define (interleave lst1 lst2) 
    (cond
        ((equal? lst1 nil) lst2)
        ((equal? lst2 nil) lst1)
        (else (append (list (car lst1) (car lst2)) (interleave (cdr lst1) (cdr lst2)))) 
    )
)
; 去除 list s 中的重复元素
; eg. (no-repeats (list 5 4 5 4 2 2)) = (5 4 2)
(define (no-repeats s) 
    (define (filter pre now)
        (cond
            ((equal? now nil) nil)
            ((= pre (car now)) (filter pre (cdr now)))
            (else (append (list (car now)) (filter pre (cdr now))))
        ) 
    )
    (cond
        ((equal? s nil) nil)
        (else (append (list (car s)) (filter (car s) (no-repeats (cdr s)))))   
    )
)

异常(exception)
未处理的异常会导致 Python 程序停止运行, 解释器将打印一个堆栈回溯(stack backtrace)
异常也是一种对象, 其类有对应的构造函数
抛出异常(raising an exception): assert 语句会抛出一个类为 AssertionError 的异常, 格式为 assert <expression>, <string>。
通常情况下, 可以使用 raise 语句来抛出任何异常实例, eg. raise Exception('An error occurred')
处理异常(handling exceptions): 异常可以由封闭的 try 语句来处理。try 语句由多个子句组成；第一个以 try 开头，其余的以 except 开头:

try
	<try suite>
except <exception class> as <name>:
	<except suite>

我们先执行 <try suite>, 如果有抛出异常且异常类型为 <exception class>, 则 <except suite> 会强制执行, 并把 <name> 绑定到异常上

>>> def invert(x):
		result = 1/x  #抛出一个异常（ZeroDivisionError) 如果 x 为 0
		print('Never printed if x is 0') 
		return result
>>> def invert_safe(x):
		try:
			return invert(x)
		except ZeroDivisionError as e:
			return str(e)
#-----------------------------------------
>>> invert_safe(2)
Never printed if x is 0
0.5
>>> invert_safe(0)
'division by zero'

让我们回到 scheme, 下一步目标是做一个 scheme 程序的解释器
解析是根据原始文本输入生成表达式树的过程。解析器由两个组件组成: 词法分析器(lexical analyzer)和语法分析器(syntactic analyzer)
首先, 词法分析器将输入字符串划分为标记(token)。标记表示语言的最小语法单元, 比如名称和符号。然后, 语法分析器根据这个标记序列构建一个表达式树。

>>> tokenize_line('(+ 1 (* 2.3 45))') #lexical analyzer part
['(', '+', 1, '(', '*', 2.3, 45, ')', ')']
>>> expression = scheme_read(Buffer(tokenize_lines('(+ 1 (* 2.3 45))'))) 
>>> expression #syntactic analyzer part
Pair('+', Pair(1, Pair(Pair('*', Pair(2.3, Pair(45, nil))), nil)))
>>> print(expression)
(+ 1 (* 2.3 45))

让我们先尝试做一个 scheme 计算机, 主要依赖于 Pair 类来实现

将一个表达式变成 pair 的形式有助于解释器(interpreter)处理
scheme_eval 函数用于对 Scheme 中不同形式的表达式进行求值, 包括基元、特殊形式和调用表达式。在 Scheme 中, 组合形式可以通过检查其第一个元素来确定。每种特殊形式都有自己的求值规则

我们要特殊关心那些逻辑语句, 它们会带来一个或多个子表达式, 例如 if,and,or,cond:

再学一下引用(quotation), (quote <expression>) 后编译器回处理出来 <expression>, 再处理一次才能得到表达式的值, 相当于单引号的作用 (quote (1 2)) 和 `(1 2) 是等价的

现在我们已经描述了 Scheme 解释器的结构, 接下来我们来实现构成环境的 Frame 类。每个 Frame 实例代表一个环境, 在这个环境中, 符号与值绑定。一个帧有一个保存绑定(bindings)的字典, 以及一个父(parent)帧。对于全局帧而言, 父帧为 None
绑定不能直接访问，而是通过两种 Frame 方法：lookup 和 define。第一个方法实现了第一章中描述的计算环境模型的查找流程。符号与当前帧的绑定相匹配。如果找到它, 则返回它绑定到的值。如果没有找到, 则继续在父帧中查找。另一方面，define 方法用来将符号绑定到当前帧中的值, 格式为 (define <name> <expression>) 为了说明 lookup 和 define 的用途，请看以下 Scheme 程序示例:

(define (factorial n)
  (if (= n 0) 1 (* n (factorial (- n 1)))))

(factorial 5)
120

第一个输入表达式是一个 define 形式, 将由 Python 函数 do_define_form 求值。定义一个函数有如下步骤:

1. 检查表达式的格式, 确保它是一个格式良好的 Scheme 列表, 在关键字 define 后面至少有两个元素
   
2. 分析第一个元素(这里是一个 Pair), 找出函数名称 factorial 和形式参数表 (n)
   
3. 使用提供的形式参数、函数主体和父环境创建 LambdaProcedure
   
4. 在当前环境的第一帧中, 将 factorial 符号与此函数绑定。在示例中, 环境只包括全局帧

第二个输入是调用表达式。传递给 scheme_apply 的 procedure 是刚刚创建并绑定到符号 factorial 的 LambdaProcedure。传入的 args 是一个单元素 Scheme 列表 (5)。为了应用该函数, 我们将创建一个新帧来扩展全局帧 (factorial 函数的父环境)。在这帧中，符号 n 被绑定为数值 5。然后, 我们将在该环境中对 factorial 函数主体进行求值, 并返回其值。

本部分笔记最重要的解释器编写在我的 Scheme 大作业中, 缺少它会失去很多乐趣 =)
大作业有一个 Optional Problem: 实现 Scheme 解释器中的尾调用(Tail Call)优化

在计算机学里, 尾调用(tail call)是指一个函数里的最后一个动作是返回一个函数的调用结果的情形, 即最后一步新调用的返回值直接被当前函数的返回结果
尾调用由于是函数的最后一步操作, 所以不需要保留外层函数的调用记录, 因为调用位置、内部变量等信息都不会再用到了, 只要直接用内层函数的调用记录, 取代外层函数的调用记录就可以了

以阶乘函数的两种实现为例:

# tail-recursion
def factorial_recursion(n, k):
    if n == 0:
        return k
    else:
        return factorial(n - 1, k * n)

# iteration
def factorial_iteration(n, k):
    while n > 0:
        n, k = n - 1, k * n
    return k

递归版本具有更高的空间复杂度, 在 n 较大时会爆栈

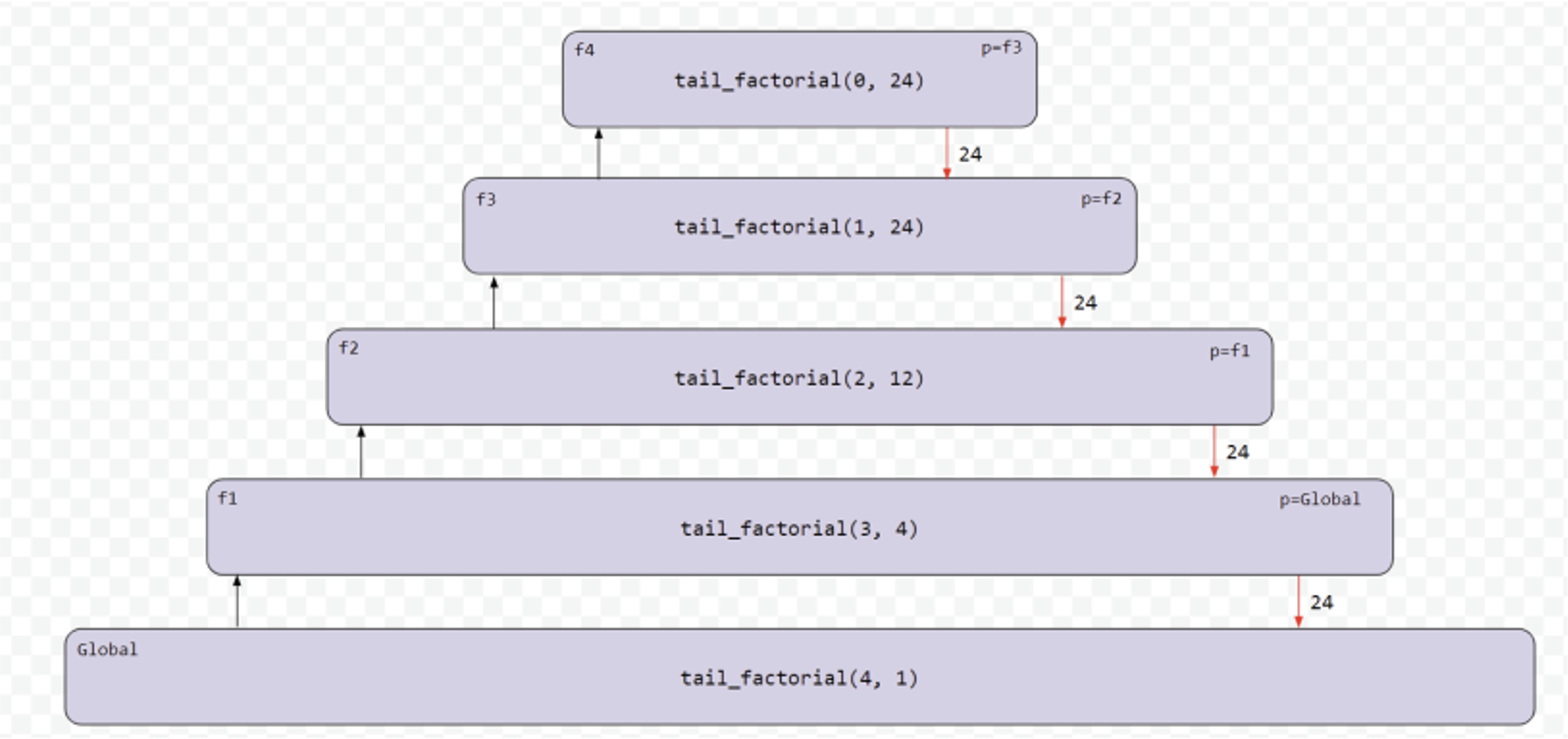
所以我们想到不保留栈帧, 递归到下一层时将变量保存过去即可:

def thunk_factorial(n, so_far=1):
    def thunk():
        if n==0:
            return so_far
       	return thunk_factorial(n-1, so_far*n)
    return thunk

def factorial(n):
    value = thunk_factorial(n)
    while callable(value):
        value = value()
    return value

图例是这样的:

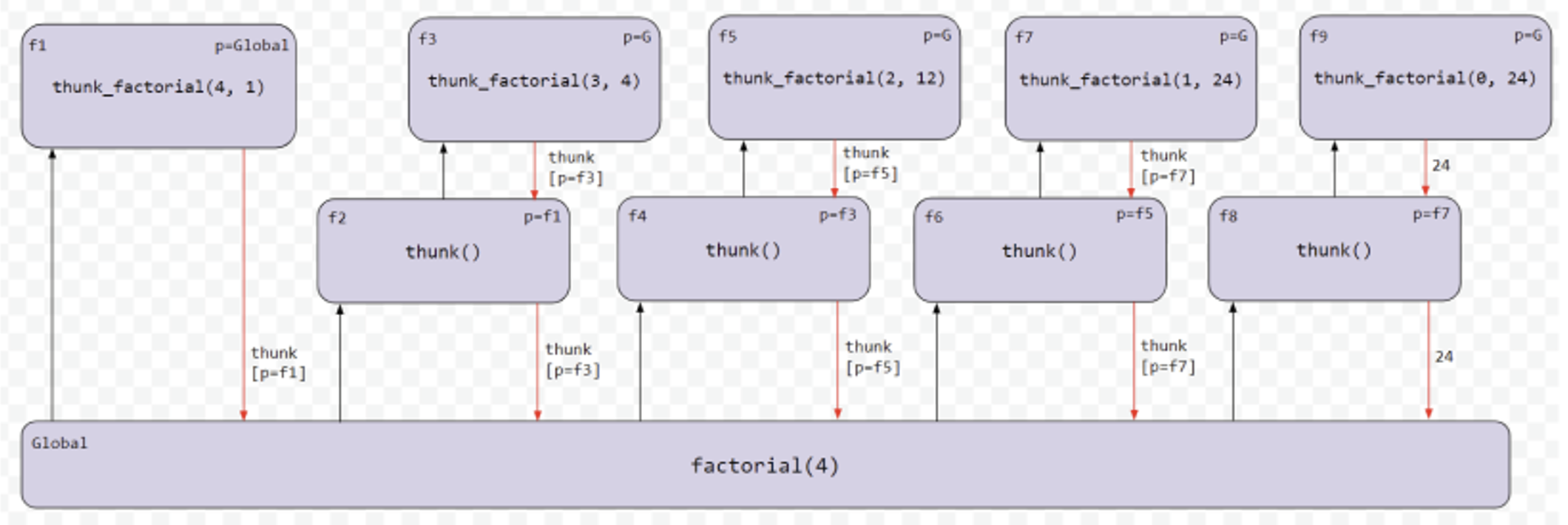
在 scheme 解释器中的优化是这样的:

def optimize_tail_calls(unoptimized_scheme_eval):
    """Return a properly tail recursive version of an eval function."""
    def optimized_eval(expr, env, tail=False):
        """Evaluate Scheme expression EXPR in Frame ENV. If TAIL,
        return an Unevaluated containing an expression for further evaluation.
        """
        if tail and not scheme_symbolp(expr) and not self_evaluating(expr):
            return Unevaluated(expr, env)
        # Unevaluated 即类似上图的 thunk() 
        result = Unevaluated(expr, env)
        while isinstance(result, Unevaluated):
            result = unoptimized_scheme_eval(result.expr, result.env)
        return result
    return optimized_eval

tail 即代表到达了底部, 返回函数值, 否则先返回一个 Unevaluated 实例回收空间, 在 result 的环境中计算表达式, 反正不能到最后才回溯就是了

数据处理

声明式编程(英语：Declarative programming)或译为声明式编程, 是对与命令式编程不同的编程范型的一种合称。它们建造计算机程序的结构和元素, 表达计算的逻辑而不用描述它的控制流程

即告诉计算机做什么而不是编写代码教计算机怎么做

SQL 是一种声明式编程语言的例子。SQL 语句不直接描述计算过程, 而是描述一些计算的预期结果。数据库系统的查询解释器负责设计和执行计算过程以产生这样的结果

可以使用 SQL 语言中的 select 语句创建一个单行表, 其中行值用逗号分隔, 列名跟在关键字 "as" 后面。所有的 SQL 语句都以分号结尾, eg. select [expression] as [name], [expression] as [name]

select 38 as latitude, 122 as longitude, "Berkeley" as name;
38|122|Berkeley
-- 当然实际显示没有这么简陋, 可以去 vscode 上下载一个 sqlite 插件, 新建 .sql 文件, run query 玩一下

多行要用 union 连接

select 38 as latitude, 122 as longitude, "Berkeley" as name union
select 100,71,"Cambridge" union
select 45,93,"Minneapolis";

latitute	longtitude	name
38	122	Berkeley
100	71	Cambridge
45	93	Minneapolis

select 语句只是拿来显示而不是存储, 存储用 create table [name] as [select statement]

create table cities as
    select 38 as latitude, 122 as longitude, "Berkeley" as name union
    select 42,             61,               "Cambridge"        union
    select 45,             93,               "Minneapolis";
SELECT * FROM cities; -- 验证表结构和数据

select 语句可以通过列出单行的值或更常见的通过在 from 子句中使用现有表来定义一个新表 (现有表投影)
select [column name] from [existing table name]
更复杂一点的, 有:
select [column name] from [existing table name] where [condition] order by [order]
eg. select name, latitude, temp from cities, temps where name = city;

还可以写一些算数式子, 以课程中的图举例:

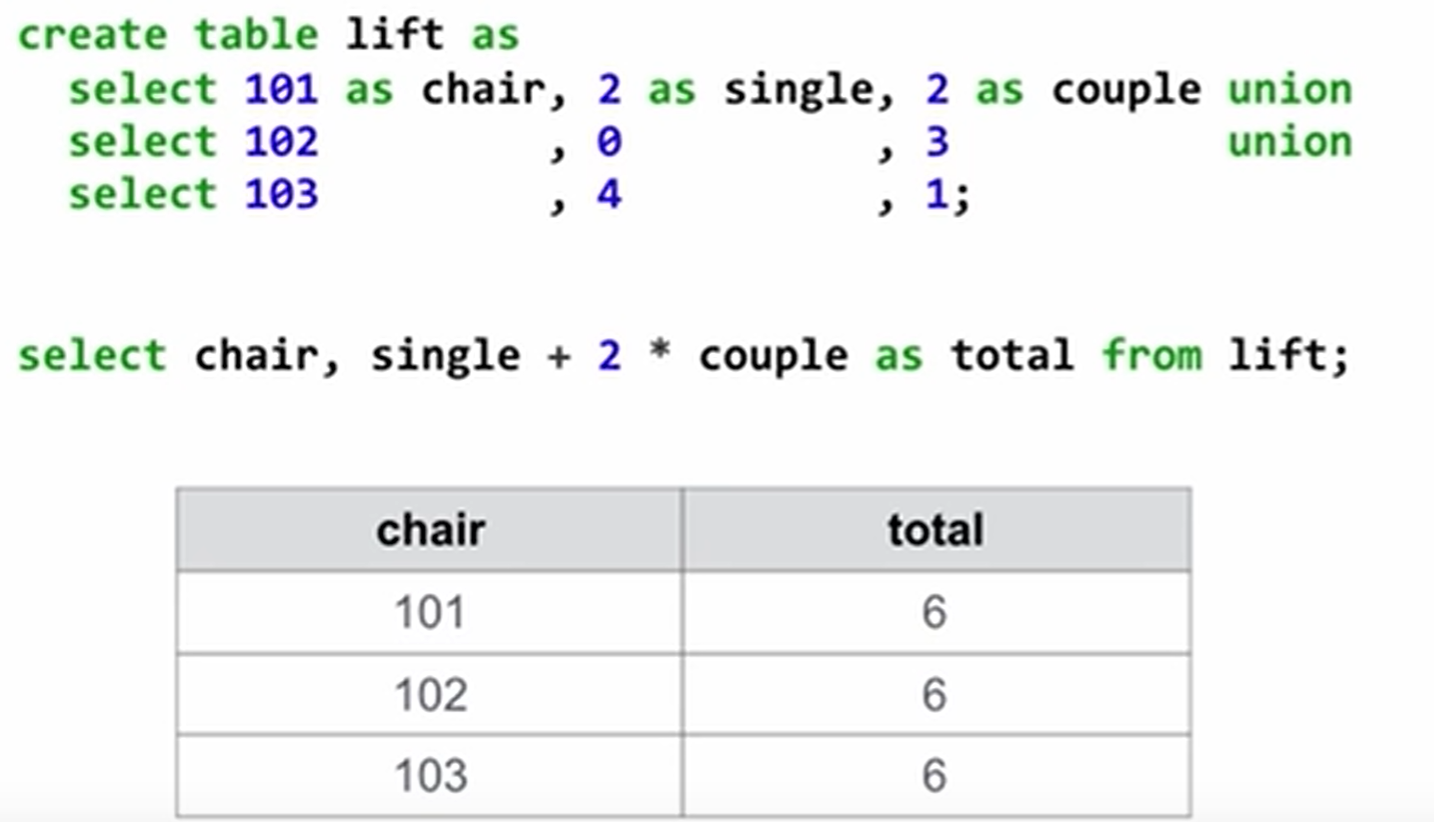
合并表信息:
如果直接连接, select * from A, B; , 若 A 表有 m 行, B 表有 n 行, 则新表有 m*n 行
一般来讲我们只 select 我们需要的行, 还要加上一些 where [condition] 来限制它
有时候表的某个列名我们需要导入多次分别使用, 我们可以给相同的列名取一些别名(aliases)

select a.child as first, b.child as second
	from parents as a, parents as b
	where a.parent = b.parent and a.child < b.child
-- 一段找兄弟姐妹的程序

string 表达式:

select "hello, " || "world";
hello, world

有一些函数可以用, 比如说 substr 和 instr, 用到再查

create table nouns as
    select "dog" as phrase union
    select "cat"           union
    select "bird";

select subject.phrase || " chased " || object.phrase as phrase
    from nouns as subject, nouns as object
    where subject.phrase <> object.phrase; 
-- <> 即为不等于号
phrase
bird chased cat
bird chased dog
cat chased bird
cat chased dog
dog chased bird
dog chased cat

limit [number] 可以限制输出的条目数目, 一般放在最后

聚合函数(aggregate functions)
max() / min() / sum() / avg() / count()(返回行数) / ......

聚合函数会选择对应的行, 当写出 select max(A), B from All 这样的代码时, 只会返回 max(A) 所在的那一行 但是当你写一些更抽象的东西, 比如 select avg(A), B from All, 返回什么只有天知道了

select 语句默认都在一个大的聚合(group)里, 我们可以给这些 select 语句加上分类, 这样聚合函数会对每个聚合进行运算, 并输出多行结果, 格式:
select [columns] from [table] group by [expression] having [expression]

eg. select legs, max(weight) from animals group by legs

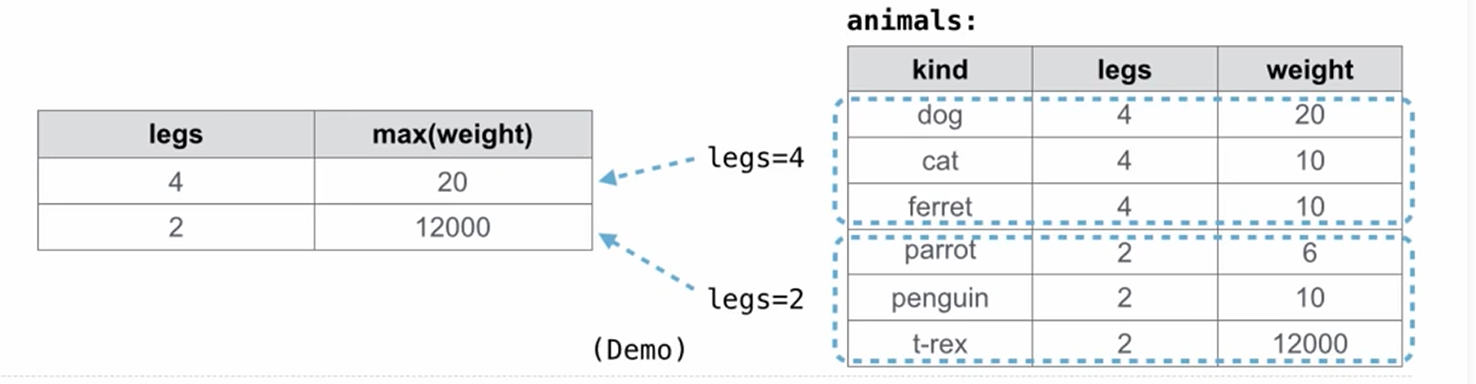
之后课本上还有一些内容, 比如分布式计算和并行式计算, 可惜没有课程了, 相关内容可能以后会补充到笔记中