Codeforces exercises 2024
记录了24/7/8-24/12/28的十八场 codeforces 补题, \(rating\;1646\rightarrow1785\)
Undone: 982 的 E 还没写完, 后补
codeforces round 956 (#Div2) 24/7/8
\((1646 \rightarrow 1692,
rk1180)\)
\(next\_permutation\)
不会用导致卡了40mins C, 认了
E
题意:
Alice 和 Bob 轮流随机取球, 一共 \(n \leq 4
\times 10^5\) 个带有一定分值 (\(v_i\)) 的球, 前 \(k\) 个特殊球取了之后还能继续取球,
效果可叠加, 问 Alice 先手情况下两人得分的期望 (模 \(10^9+7\) 输出)。
思路:
小巧精妙的题。分 \(n-k\) 个普通球和
\(k\) 个特殊球来思考,
先求出各自种球分值的和。对于普通球, Alice 一定会取 \(\lceil \frac {n-k}{2}\rceil\) 个。
对于特殊球取的个数, 因为其与普通球有关, 一个直观的想法是 D。设 \(dp_{i,j}\) 表示此时有 \(i\) 个普通球, \(j\) 个特殊球时取走的特殊球数量的期望,
显然其可以通过 \(dp_{i-1,j},
dp_{i,j-1}\) 转移而来, 很可惜这个想法是 \(O(n^2)\) 的, 我们可以以此辅助先打表试试
(当然前提是你C++有一个分数类的模板或你略懂 python) 。
我们发现, 除最后一次取球外, 一个人的完整的一次取球必定以取普通球结束
(n个连续的特殊球加上一个普通球),
我们可以采用配凑的手段在取球序列的最后加上一个普通球, 这 \(n-k+1\) 个普通球将整个取球序列分为 \(n-k+1\) 段,
每一个特殊球出现在每一段中的概率都是相等的, 而 Alice 会取走 \(\lceil \frac{n-k+1}{2} \rceil\) 段,
所以会取走 \(k \times \frac{\lceil
\frac{n-k+1}{2} \rceil}{n-k+1}\) 个特殊球,
剩下的就是一个逆元板子了。
代码: link
codeforces round 958 (#Div2) 24/7/15
\((1692 \rightarrow 1642,
rk3656)\)
乱用 define int long long 加上D题思路错误, 认了
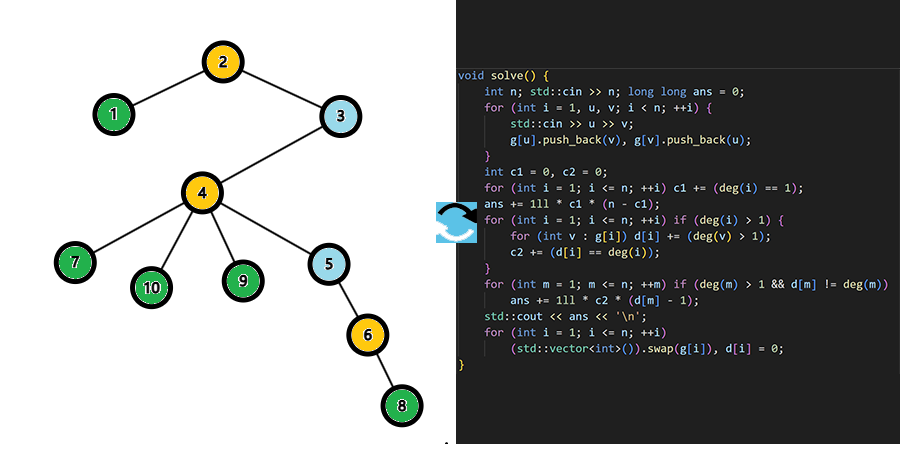
D
题意:
树, 点有权值, 每回合先收到树上权值和(\(\sum
{a_{i}}\))的伤害, 然后可以删去任意多不在一条边上的点,
问受到的最小总伤害。(\(n \leq 3 \times 10^5,
a_i \leq 10^{12}\))
思路:
一开始认为总轮数最多为 3 , 否则会在第一次删点后在树上形成长度大于等于 3
的长链, 那么中间的点就应该第一轮被删去, 这个思路是错误的, 反例很好举:
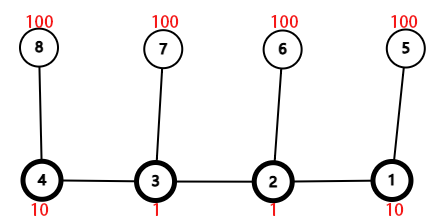先删5 6 7 8, 再删 1 4, 再删 2, 再删 3。
所以思考最多要几轮删完: 设第 \(i\)
个点第 \(b_i\) 轮被删,
题目限制等价于不存在相邻的两个点 \(b_i\) 相同, 在最优情况下, \(b_i = mex_{(j,i) \in E} b_j\) , 设最大的
\(b_i = u\) , 使其为根节点, 其子节点的
\(b_j\) 遍历 (1~ u-1) , 这样递归推下去,
可推得 \(u= \lfloor log_2n \rfloor +1\)
。
在真实比赛中, 我们可以根据最大权值和 \(3
\times 10^5 \times 10^{12} \leq 10^{18}\), 以及 \(2^{60} \; >\; 10^{18}\) ,
构造出一种最多删 60 轮的删法, 即每次将树黑白染色后删较大权值和的部分,
直接根据 \(u \leq 60\) 来 DP。
设 \(f_{i,k}\) 表示以 \(i\) 为根的子树全部删完且 \(i\) 节点在第 \(k\) 轮删去的受伤害最小值, 即有 \(f_{i,k}=k \times a_{i} + \sum\limits_{(i,j)\in E}
min\{f_{j,1},f_{j,2},...,f_{j,k-1},f_{j,k+1},...f_{j,60}\}\)
前缀和后缀和做一下即可快速更新, 复杂度 \(O(60n)\)
代码: link
codeforces round 959 (#Div1+2) 24/7/18
\((1642 \rightarrow 1631, rk3146)\)
D
题意:
给你 \(a_i\) 数组, \(n-1\) 次操作, 第 \(x\) 次操作时若 \(x\) 整除\(|a_u-a_v|\) 则可连边, 问能不能连成一棵树,
\(n \leq 2000, a_i \leq 10^9\)
思路:
鸽巢原理, 反着操作, 第 \(x\) 次操作时有
\(x+1\) 个连通块,
则一定有两个连通块中的两个数关于 \(x\)
同余, 加个并查集即可通过本题
代码: link
E
幽默贪心, 个人 D > E, 题解区有人说应该把 E 放在 C 位置上的
codeforces round 960 (#Div2) 24/7/20
\((1631 \rightarrow 1695,
rk950)\)
E = 2500, 先咕着, 等我上 2000 就回来补。 ---24.9.29
Pinely round 4 (#Div1+2) 24/7/28
\((1695 \rightarrow 1709, rk2176)\)
E
题意：
交互题, 给定无向图和三种颜色 \(1, 2,
3\), Alice 和 Bob 进行游戏, 每一轮:
- Alice 选择两种不同颜色
- Bob 选择其中一种颜色并选择一个未染色点染色
如果 \(n\) 轮后, 有相邻节点颜色相同,
则 Alice 胜利, 否则 Bob 胜利, 请输出胜者并完成交互
思路:
一个观察: 只要有奇环 Alice 就获胜, 否则 Bob 获胜。
一开始想要把图的奇环取出来, 比较困难
一个更进一步的观察: 若选择 Alice 胜利来交互, 只要重复选择颜色 \(1,2\) 就行了,
所以只用黑白染色确认奇环的存在就行。对于 Bob 胜利的情况,
我们刚刚染好色的图就派上用场了, 如果 Alice
给了对应染色的颜色就选那种颜色的点染色, 否则直接选择颜色 3, 此时 \(1, 2\) 种肯定有一种颜色染完了,
就染剩下颜色对应的点。
代码: link
F
题意：
给你 \(n\) 根棍子, 长度 \(a_i\) , \(q\) 次询问, 每次问 \([l,r]\;(r-l+1\geq 6)\)
的范围中能不能取六根棍子组成两个三角形。
\(n, q \leq 10^5, a_i \leq 10^9\)
思路:
纯纯诈骗题,
一个最优的思想肯定是将所给区间排好序后尝试选择相邻的棍子构成三角形,
这样暴力做一次的代价是 \(O(nlogn)\)
的。我们注意到 \(a_i \leq 10^9\),
尝试构造一个构造不出来三角形的最长数列, 即 \(1,1,2,3,5,8,13,...\) 事实上四十多项就涨破
\(10^9\) 了, 于是我们对于那些过宽的区间
\([l,r]\) 缩到最多 \(50\) 的长度, 这样单次代价 \(O(50log(50))\), 可以通过本题。
如果这题的样例没有精心构造过, 这题会从诈骗题晋升为钓鱼题。对于 \(\{2,2,4,5,10,10\}\) 这个样例, 里面 \(\{2,4,5\}\) 是连续的, \(\{2,10,10\}\) 不是连续的,
这告诉我们答案可能会从连续的 \(6\)
个数字中不连续的出来, 设 \(6\)
个数字从小到大为 \(a,b,c,d,e,f\) ,其中
\(a\) 一定为短边, \(f\) 一定为长边, 要检查一共七种可能情形,
分别是:
- \(a+b>d,\;c+e>f\)
- \(a+c>d,\;b+e>f\)
- \(b+c>d,\;a+e>f\)
- \(a+b>e,\;c+d>f\)
- \(a+c>e,\;b+d>f\)
- \(a+d>e,\;b+c>f\)
- \(b+c>e,\;a+d>f\)
对于 \(\{1,2,2,4,6,10,10\}\)
这个样例, 里面的 \(\{1,2,2\}
,\{6,10,10\}\) 并没有接到一起去, 但是是各自连续的,
这启示我们答案可能由两个不在一起的 "三连续子数组" 构成,
可证明只存在这两种构成方式。
代码: link
codeforces round 963 (#Div2) 24/8/4
\((1709 \rightarrow 1661, rk3739)\)
D
绝妙思维题, 告诉我们题目的每个条件都应尽量贴切用上,
可能还是我见的太少了......
题意:
给你长度为 \(n\) 的数组 \(a_i\) 和常数 \(k\) , 每次在数组中删掉长度为 \(k\) 的连续段直到不能删为止,
问剩下数列的中位数最大是多少？ \(n,k \leq
5*10^5, a_i \leq 10^9\)
思路:
首先套一个二分, 中位数根据与 mid 的关系映射为 \(-1/1\) , 再套一个前缀和。
接下来我的想法是贪心暴力, 先把目前能删的连续段都放进优先队列里,
若删去一个段再考虑把它两边接起来的段继续扔进去, 需要一个双向列表来维护,
难写得很, 复杂度大抵是对的, 但是过不了题。
题解思路利用了一个条件, 每次删除的连续段长度不变, 都是 \(k\), 假设删到最后剩下 \(x\) 个数, 它们下标 \(mod\;k\) 的结果一定是 \(1,2,3,...,x\)
,这样就可以通过下标判断选了几个数从而 \(dp\) , 设 \(f_u\) 表示最后一个数字 \(mod\; k=u\) 的答案, 转移一下就行了。
代码: link
codeforces round 965 (#Div2) 24/8/10
\((1661 \rightarrow 1672, rk2013)\)
EPIC Institute of Technology Round August 2024 (#Div1+2) 24/8/11
\((1672 \rightarrow 1797, rk773)\)
D2
是 \(\color{black}{\tt{B}}\color{red}{\tt{rothercall}}\)
的思路, 不是我的, 谢罪, \(\color{black}{\tt{B}}\color{red}{\tt{rothercall}}\)
真乃直觉杀手。
简写一下, 这题问给定排列是不是给定树的 DFS 序,
你手玩一颗树后可以猜想其充必条件为: 对于排列上所有相邻的两点, 它们的 lca
要么为前点(正在下探), 要么为后点的父节点(探完当前子树去新子树)
其必要性显然, 但充分性我真不会证
educational codeforces round 169 (#Div2) 24/8/15
\((1797 \rightarrow 1827, rk928)\)
E
题目名称 Not A Nim, 实则是 SG 函数的板子, 把这个知识漏洞补了下
codeforces round 973 (#Div2) 24/9/20
\((1827 \rightarrow 1800, rk1595)\)
D
分别做两次二分, 可证明两次互不干扰, 我想到二分套二分上去了……
E
小清新数论, 注意到 gcd 的减少至少也要缩一半 (/2), 故缩到 0 最多十次, 贪心解决, \(O(10n)\)
Educational Codeforces Round 170 (#Div2) 24/10/14
卡了三十分钟 C, 因为双指针不会写加上多测不清空, 寄之。
E
题意:
有 \(n\) 组牌, 每组牌有 \([1,m]\) 数字的牌各一张, 一人拿 \(n\times m/2\) 张牌,
然后要找这样的拿牌方案数, 规定对于一方出的任意一张牌,
另一方都有牌比它大, 每张牌只能用一次。牌的大小是这样比较的:
- 第一组的牌可以打败任意非同组的牌
- 若牌的组数相同，则比较牌的数字大小
规定 \(n,m \leq 500\) 且 \(m\) 为偶数, 方案数模 \(998244353\) 输出。
思路:
假设 \(n=1\) ,
这本质上就是个卡特兰数
若 \(n \neq 1\) ,
第一组牌的取法就成了卡特兰数的变形, 我们可以取 \(c\geq m/2\) 张牌,
在和其他第一组的牌比较完后还能剩 \(c-m/2\) 张牌给后面用(相当于万能牌了), 对于
2~n 组, 可以看出每组只能取最多 \(m/2\)
张牌, 否则多取的花不出去无法跨组比较，我们可以想到这样一个 DP:
\[
f_{i,j}=f_{i-1,j-1}+f_{i-1,j+1}\;\;\;\;f_{i,j}\;表示第1组目前取了i张牌并剩余j张万能牌
的方案数\]
\[g_i=f_{m,m-i}\;\;\;\;g_i\;表示m张卡片取i张并获得i/2场胜利的方案数(剩下m-i张用万能牌取胜)\] \[h_{i,j}= \sum\limits_{k=0}^j h_{i-1,k}*g_{m+k-j}\;\;\;\;h_{i,j}\;表示对于2\sim i 组,用过了j张万能牌的方案数\]
答案即为 \(\sum\limits_{i=0}^{m}f_{m,i}*h_{n,i}\)
复杂度 \(O(nm^2)\)
主要代码:
1 | f[0][0]=1; //f[i][j]: choose i cards and rest j cards on hand |
codeforces round 980 (#Div2) 24/10/20
\((1800 \rightarrow 1688,
rk4628)\)
寄中寄, 做完 AB 后 C 陷入了先入为主猜结论的死胡同, D 又想假了,
一场就送掉了……
D
题意:
有 \(n\) 个问题编号从 \(1\) 到 \(n\) , 每个问题有得分 \(a_i\) 和参数 \(b_i\)
从第一个问题开始决策, 每次决策有两种选择:
- 提交问题获得 \(a_i\) 分, 然后问题作废, 下一题的下标 \(j\) 是满足 \(j<i\) 且问题未作废的最大下标
- 跳过问题, 然后问题作废, 下一题的下标 \(j\) 是满足 \(j \leq b_i\) 且问题未作废的最大下标
最大化得分, 数据范围 \(n \leq 4 \times
10^5,a_i \leq 10^9, 1 \leq b_i \leq n\)
思路：
题目本身不是很难, 有优先队列(dp)解法, 大体思路是设 \(f_i\) 为到 \(i\) 点的最小花费, 更新 \(i\) 时, 找队列中 \(b_j \geq i\) 且代价最小的作为 \(f_i\) , 更新完后把 \(\{a_i+f_i,b_i\}\) 压入优先队列中,
记得开小根堆。
然而这题真正有趣的在于其图论刻画, "下一题" 类似于一种有向边,
最大化得分则是最长路, 考虑建图:
- \(i \stackrel{-a_i}{\longrightarrow} b_i\) , 表示跳过问题
- \(i \stackrel{0}{\longrightarrow} i-1\) 表示提交问题
- \(i \stackrel{\sum_{j=1}^i a_j}{\longrightarrow} 0\) 表示不再跳过问题, 按顺序回答前面的每个问题直至结束
只有跳过问题会导致分数的减少, 只有不再跳过才进行分数的结算,
故提交问题的边权为 \(0\)
代码(来源知乎):
1 |
|
codeforces round 982 (#Div2) 24/10/26
\((1688 \rightarrow 1793,
rk301)\)
手速场, D2 不会, E 是我见过最难的 SG 函数了
E1
题意:
\(n\) 堆石子, 每堆 \(x_i\) 个, 有一个限制上限 \(a_i\) , 两人先后手在一堆石子中取,
每次可以取 \(d\) 个, 满足 \(1 \leq d \leq a_i\) 且 \(x \;\&\;d=d\) 其中 \(x\) 是当且这堆石子的数量, 问理想状态下谁赢
? \(n \leq 10^4; a_i,x_i \leq
2^{30}\)
思路:
一眼 SG 函数, 但是不能只靠打表
当 \(a_i \geq x_i\) 时相当于 \(a_i\) 对 \(x_i\) 没有影响, 此时 \(sg(x_i) = popcount(x_i)\) 即 \(x_i\) 在二进制下 \(1\) 的个数。
当 \(a_i < x_i\) 时,
我们尝试归并到上面情况:
首先忽略 x 比 a 高的位数, 因为肯定取不上去, 完成 a, x 位数的对齐, 例如
a=100, x=1101 等价于 a=100, x=101
对于 a=100010, x=110000 , \(x\)
中第一个比 \(\underline{a}\)
大的位置后的 1 的数量为 0, 所以 \(x\) 不管怎么取之后 \(x' < a\) 且 \(x' \neq 0\), 所以 \(sg(x)=0\)
对于 a=100010, x=110001, 其等价于 a=100001, x=110001,
(对于 x=0, a=1的第一位, a 后面的 0 都翻成 1), 这又等价于 a=101,
x=111(去除两边都为 0 的部分), 这下子 x 被我们消成了 \(2^k-1\) 的形式
codeforces global round 27 24/10/27
\((1793 \rightarrow 1788,
rk1780)\)
每次都天真的往 D 糊一个 1400 难度的假做法, 还恰巧能过样例, 于是上头狂调,
一小时有余方才发现错误, 亡羊补牢为时已晚, 掉了小分
E
题意:
初始攻击力为 \(0\)
，进行以下操作，以最少的代价击败生命值为 \(z\) 的 Boss：
1.攻击力提升 \(1\) ，花费 \(x\) 的代价。最多连续进行
\(k\) 次攻击力提升。
2.进行一次攻击，造成相当于攻击力的伤害，花费 \(y\) 的代价。
\(1 \leq x,y,z,k \leq 10^8\), 100
组数据
思路:
一开始蒙了个三分, 认为先提升攻击最后进行攻击的击败代价函数是个二次函数,
后来发现不对劲, 因为整数的离散性需要上取整, 函数不是平滑的。
然而总体的思路不变, 先升级再打, 注意到不是每次升级攻击力都会减少回合数,
例如对于血量为 \(20\) 的 boss 而言,
只有攻击力提升到 \(1,2,3,4,5,7,10,20\)
时才会减少回合数, 可以观察到临界值个数的数量级为 \(\sqrt z\)
于是我们每次尝试拿 \(min(\sqrt z, k)\)
个临界值更新临界答案 (即加到临界值的攻击后停止提升并一直攻击的答案) ,
然后进行一次攻击, 若 boss 仍有血量并继续循环, 循环次数为 \(O(\sqrt{z/k})\) 次, 一次循环有 \(min(\sqrt z, k)\) 个临界值, 当 \(k \sim O(\sqrt z)\) 时, 复杂度为 \(O(z^{3/4})\)
代码:link
educational codeforces round 171 (#Div2) 24/10/28
\((1788 \rightarrow 1810, rk986)\)
E
题意:
给定大小为 \(n\) 的数组 \(a\), 现在让你从 \(a\) 中选取一些数, 记为数组 \(b\) , 求 \(|b|-popcount(\bigvee b_i )\) 最大值 \(T, n \leq 100, a_i \leq 2^{60}\)
思路:
十分的 educational , 最大权闭合图裸题, 设 1 ~ N 为数组各位, N+1~N+60 为
60 个二进制位, 连边:
\(S\stackrel{1}{\longrightarrow} i (i \in
[1,n])\)
\(i (i \in [1,n])
\stackrel{inf}{\longrightarrow} n+j \;\; ((a_i >> j) \&
1==1)\)
\(n+j\stackrel{1}{\longrightarrow}
T\)
答案即为 \(n-dinic()\)
代码: link
codeTON round 9 (#Div1 + 2) 24/11/23
\((1810 \rightarrow 1852, rk1139)\)
C2 过了还是很懵, 分类讨论容易把人写浑, 不要追求讨论不重,
追求不漏就可以了
E
题意:
初始 \(a=\{0,1\}\), 每次操作将 \(a\) 的逆序对个数选择插入 \(a\) 的任意位置, 求长度为 \(n\) 的 \(a\) 数组的方案数, \(n \leq 10^6\)
思路:
就不抄一遍 Tutorial 了,
思想就是分类, 递推。因为注意到当 \(a\)
的逆序对个数大于 \(a\) 的最大值时,
所有插法都是新的, 记这样的 \(a\) 为
"好数组"。于是可以先考虑一个长度为 \(i\) 的 "好数组" 可以构成多少个长度为 \(n\) 的 "好数组", 再看有多少个 "好数组"
可以由 "坏数组" 一步构造成, 答案为 "坏数组" 数量加上一个 $ a*b $
形式的东西
代码: link
codeforces round 989 (#Div1 + 2) 24/11/30
\((1852 \rightarrow 1795,
rk2503)\)
D 把一个 set 的 rbegin() 改成 begin() 就过了,
告诉我们题目要想清楚一点再写, 因为以后有你急的
codeforces round 992 (#Div2) 24/12/08
\((1795 \rightarrow
1835, rk554)\)
E 的实现丑陋，期望还在拿数列极限推，其实题目思想比较经典，可惜了
E
题意:
初始在树上选择一个非根点后开始操作, 奇数步往根跳,
偶数步可以支付一元往根跳, 否则随机跳, 给你树的形态, 进行 \(Q\) 次询问, 每次询问提供初始点和钱的数量
\(k\) ,
问跳到树根所需次数的最小期望
\(k \leq N \leq 2000, Q\leq
2000\)
思路:
考场上把一条链上的需要花钱的点抽出来按期望 sort 后毙掉花钱最多的 \(k\) 个, 但是期望算错了并且实现很丑,
实际上可以树型 DP 解决 设点 \(u\)
往上跳的步数期望为 \(P(u)\) , 有 \(P(u) = \frac{1}{son_u+1} + \frac{son_u}{son_u+1}
\times (P(u)+2)\), 解得 \(P(u) = 2
\times son_u+1\)
设 $f_{i,j} $ 表示点 \(i\) 花费 \(j\) 元跳到根节点的最小期望, 有:
\[f_{root,i} = 0,\; f_{son_{root},i} = 1,\; f_{v,0}=f_{fa_u,0}+P(u)+1 (v \notin son_{root})\]
\[f_{v,i} = min(f_{fa_u,i-1}+2,f_{fa_u,i}+P(u)+1)\]
然后 DP 即可, 复杂度 \(O(n^2)\)
代码:link
Good Bye 2024: 2025 is NEAR 24/12/28
\((1835 \rightarrow
1785, rk3180)\)
纯纯小丑，D 一眼题却实现丑陋，WA
的要道心破碎了，果然以后有我急的，应该以后还有我急的。 E
看上去挺漂亮
E
题意:
给定一棵大小为 \(N\) 的树, 定义 \((p,q)\) 为树上 \(p,q\) 之间的路径, 在每一回合, Alice
可以选择一个连接 \(p\) 且不在路径上的点
\(u\) , 并将整个路径向 \(u\) 方向移动, Bob 可以选择一个连接 \(q\) 且不在路径上的点 \(v\) , 并将整个路径向 \(v\) 方向移动。当任何时刻 \(p\) 为度数为一的节点时, Alice 获胜,
当任何时刻 \(q\) 为度数为一的节点时,
Bob 获胜, 否则平局。问有多少个有序对 \((p,q)\) 能让 Bob 获胜？\(N \leq 200000\) 思路:
考场上想出来了 80%, 场下找到了实现方式, 觉得自己思路比较自然(抽象),
所以分享一下。
让我们定义度数为一的点为叶子节点(一类点), 连接其的点为二类点,
若都不是即为三类点。
有一种明显对答案的贡献方式, 即 \(p\)
为非一类点, \(q\) 为一类点, 所以 Bob
上来就赢了
让我们想想还有什么方式能对答案贡献, 若 \(p\) 为一类点或二类点肯定不行, 当 \(p\) 为三类点时, 在 Alice 走完一步后, 若
\(q\) 变成二类点, 则 Bob 可以向 \(q\) 连接的一类点走一步来获得胜利。
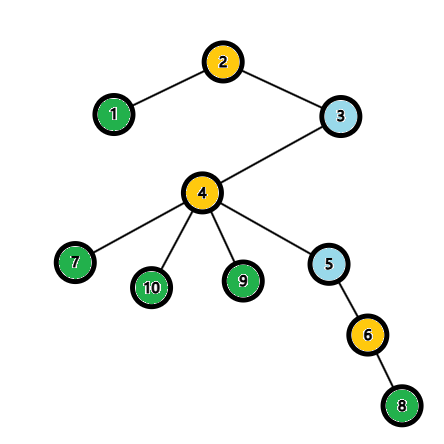
如样例四的图: 绿色为一类点, 黄色为二类点, 青色为三类点, 答案为 \(5 \times 5 + (3,5) + (5,3) = 27\)
我们要想办法统计每个作为三类点的 \(p\)
对答案的贡献, 若 \(q\) 在 \(p\) 的子树中, 不难发现 \(p\) 会使 \(q\) 上移为其父节点; 若 \(q\) 不在根到 \(p\) 的路径上, \(q\) 也会上移为其父节点; 若 \(q\) 在根到 \(p\) 的路径上, 则 \(q\) 会朝 \(p\) 方向下移。 上移的方向是确定的,
而下移的方向因 \(p\) 而异,
这启示我们先统计每颗子树的上移贡献情况, 再在 dfs 时处理根到 \(p\) 的路径。
代码的实现用了三次 dfs (尽显幽默): 第一次处理一、二、三类点;
第二次处理 \(num[x]\) , 即以 \(x\)
为根的子树中有多少非一类点的父节点为二类点; 第三次处理统计贡献。
同时, 可以注意到我一直在用一类点的定义而非 “叶节点”,
因为如果从随意一点开始 dfs 的话根节点可能也为一类点,
在代码中我寻找第一个度数 \(\geq 2\)
的点开始 dfs, 特判一下 \(N=2\)
的情况。
代码:
1 |
|
其中 isl[x] 代表一类点, isu[x] 代表二类点,
in[x] 为度数, to[x] 代表非一类点的 \(x\) 上探是否为二类点, num[x]
为以 \(x\)
为根的子树中有多少非一类点的父节点为二类点。
第三次 dfs3 中的 cur 变量代表当前子树外的统计情况,
贡献答案的时候还要加入当前子树, 并记得把 \(x\) 的情况扣掉, 因为 \(p \neq q\)
在理解上文的情况下我们可以看见官方题解更简单的做法, 我们能注意到一个更强的事实, 假设三类点总数为 \(c\), 一个二类点 \(x\) 相邻的非一类点数量为 \(m\) , 则这个二类点会对答案产生 \(c \times (m-1)\) 的贡献, 因为对于任意三类点 \(p\) , 考虑 \(q\) 在移动后到达该二类点 \(x\) , 总存在唯一的 \(q\) 在 \((p,x)\) 路径上不合法, 而其他点都是合法的且移动方向正确, 这样我们也不用弄什么 dfs 了, 直接统计即可。
我把官方题解代码也放在了下面并加上一点我的注释:
1 |
|
Codeforces exercises 2024