Codeforces exercises 2022
记录了22/5/31-22/11/20的三十七场 codeforces 补题, \(rating \;1568\rightarrow1906\)
codeforces round 795 (#Div2) 22/5/31
\((1568\rightarrow1532,
rk3394)\)
这几场都打的很寄, 例行只会ABC,
stl不会用,场上一共寄了六发,都是各种边界条件……
D
题意:
给定长度为 \(n\) 的数组 \(a (-10^9\leq a_{i} \leq 10^9)\),
问是否能找到一段区间 \([L,R]\) 使得
\(max([L,R])<\sum\limits_{i=L}^{R}a_{i}\)
思路:
区间的选择有 \(n^2\) 种,
区间最大值的选择只有 \(n\) 种,
因此要枚举所有的 区间最大值, 然后让包含它的区间最大。
流程:
\(1.\) 单调栈找到每个 \(a_{i}\) 第一个左边比它大的数 \(L_{i}\) 与右边比它大的数\(R_{i}\) \(2.\) 对 \(a\) 做前缀和, 对 \(pre\) 建线段树, 找到 \([i,R_{i}-1]\) 中的最大值和\([L_{i},i-1]\)中的最小值, 两个相减得到包含
\(a_{i}\) 的最大区间。
代码注意:线段树下标从 \(0\) 开始,
记得开 \(long\) \(long\)
代码:
1 | for(int i=1;i<=N;i++) l[i]=r[i]=0; top=0; |
是个好题, 告诉我们做题要找简单切入点, 不要盯着 \(n^2\) 的区间选择看……
E
题意:
\(N\) 条线段, 两种不同的颜色,
若不同颜色的线段有交集则说明是联通的(一个交点也算),
问有多少个连通块。
思路:
好想,难写(对于我这个不会用STL的菜鸡)。
暴力连边 \(O(N^2)\) 不可取,
尝试排序线段端点,带删连边。
我们可以把一条线段拆成左右两端点, 到左端点时加入, 右端点时删除, 存入两个
\(set\) 中(代表两个不同颜色),
加入左端点时, 若另一个 \(set\)
中还有元素(另一个 \(set\)
中的线段都包含这个左端点), 则全部合并, 因为全部合并, 可以将另一个 \(set\)
中的元素删除到仅剩一个右端点最大的元素为止, 最后统计连通块数目。
代码:
1 | struct seg {int l, r, col, pos;}; |
有几点想说:
1、\(auto\) 真好用, \(set\) 真香, 这里 \(pair\) 换 \(struct\) 也可以, 记得 \(set\) 里存的右端点。
2、代码是改 \(tourist\) 的, 在拆端点时记得给左边赋 \(-i\) ,因为有一个交点也算连通块。
3、这题拖了一个月, 因为一开始 STL 蛋都不懂。
codeforces round 796 (#Div2) 22/6/3
\((1532\rightarrow1639,
rk438)\)
全场贪心(指我会的ABCD), 猜了一个结论, E最小生成树全忘了, 到时候复健一下,
F很有趣, 但不会。场上只寄了一发F, 但A题写了19mins,
下次思考完再动手……
E (Div1 B)
复健了一下……
交互题 题意:
\(N\) 个点, \(M\) 条边的图(不一定联通), \(2M\) 次询问, 每次自由加一些边,
告诉你最大生成树林的边权和, 你要最后回答最小生成树林的边权和。
思路:
先用 \(M\) 个类似 \(0000...0010...0000\)
的字符串求出每一条边的边长, 从小到大排序一下, 再贪心 \(M\) 次尝试一条条加回去,
如果加回去后返回的最大森林边权和等于目前的答案加上加入的那条边的边权,
则说明新加入的这条边联通了两个块, 应该保留, (类似 \(kruskal\) 的思想), 最后输出答案。
代码:
1 | N=read(); M=read(); |
F (Div1 C)
题意:
给定两个长为 \(n\) 的数组 \(a\), \(b\), 再给 \(m\) 个区间 \([l_{i}, r_{i}]\) , 每次操作可以选择一个
\(\sum\limits_{j=l_{i}}^{r_{i}}a_{i}=\sum\limits_{j=l_{i}}^{r_{i}}b_{i}\)
的区间, 把 \(b\) 的这部分换到 \(a\) 上, 问能否通过若干次操作将 \(a\) 换成 \(b\)。
思路:
先是套路部分的题意转换, 区间相等\(\implies\)做前缀和. 令 \(c_{i}=a_{i}-b_{i}\) , \(pre_{i}=pre_{i-1}+c_{i}\) , 题意转化为当某个 \(pre_{l_{i}-1}=pre_{r_{i}}\) 时将 \([pre_{l_{i}},pre_{r_{i}}]\)全部赋为 \(pre_{l_{i}-1}\)(因为此时\(c_{i}=a_{i}-b_{i}=0\), 前缀和不再变化), 我们要使得最后 \(pre\) 数组清零。
一个 \(key\;observation\) 是我们要贪心的选取满足 \(pre_{l_{i}-1}=pre_{r_{i}}=0\)的可操作区间, 注意到这样的操作会使得\([pre_{l_{i}},pre_{r_{i}}]=0\), 然后我们继续寻找可操作区间。
为什么这样做是对的?我们最终的目标是全部置 \(0\), 如果一个位置 \(pre_{i}\neq0\), 要想把这个位置置 \(0\), 一定存在一个 \([l_{j}, r_{j}]\)包含位置 \(i\) 且 \(pre_{l_{j}-1}=pre_{r_{j}}=0\)
流程:
贺的题解代码, 现学现卖用 \(set\) 维护尚不能更新的区间
\(1.\) 读入, 前缀和, 不能用的点 ( \(pre_{i}\neq0\) ) 放 \(set\) 里, 能用的点压入 \(queue\), \(vector\) 存一下每个点作为起点或终点时对应的起点终点。
\(2.\) \(iterator\;lower\_bound\) 维护一下, 找到可更新的区间就把 \(set\) 里区间里的点压进 \(queue\) 中, 若最终 \(set\) 为空则说明可行。
代码:
1 | N=read(); M=read(); |
注意 \(iterator\) 不要原地删除后再跳……
codeforces round 800 (#Div2) 22/6/16
$(1639, rk574) $
C, D玄学猜结论过题, E 题真是人类智慧好题, 但我不会.
E (Div1 C)
题意: 给出一个有向图起点为 \(1\), 终点为 \(N\), 每次操作可以删去一条边或者随机选择一条边移动,问最优的操作下从起点移动到终点至多要多少步。
思路:
定义 \(dis_{u}\) 为 \(u\) 到 \(N\) 所需的最小边数, 对于一个 \(u\) 的子节点 \(v_{1}, v_{2},\cdots, v_{m}\) 有 \(dis_{v_{1}}, dis_{v_{2}},\cdots,
dis_{v_{m}}\), 设 \(dis_{v_{1}},dis_{v_{2}},\cdots,
dis_{v_{m}}\) 升序排列, 保证选到 \(v_{j}\) 或更优就要删掉 \(dis_{v_{j+1}},dis_{v_{j+2}},\cdots,
dis_{v_{m}}\) 这 \(m-j\)
条边.
我们反向建图, 可以保证每次更新的节点都是正向图中未被更新的 \(dis\) 最小的, 具体如例图:

最短路算法会先跑到 \(v1\) , 再到 \(v2\) , 再到 \(v3\) , 我们把边权设为入点 \(u\) 还没走过的子节点数 \(+1\) 跑 \(dijkstra\) 就是最后的答案.
代码( \(dijkstra\) 记录 \(in\) 数组):
1 | //dijkstra part...... |
codeforces round 801 (#Div2) 22/6/18
$(1697, rk1030) $
D 题真是人类智慧好题(下次我怕不是要夸 C 题了), 但我还是不会
想 rush 出 D 的 easy version, 失败了, 上小分
这次ABC做得都不顺, 属于真实水平暴露了
D1
题意:
无根树上一个隐藏的顶点 \(x\) ,
每次问询你可以知道被问询点与隐藏点 \(x\) 在树上的距离, 给你树的结构,
让你找出最小的问询次数 \(k\)
使得一定存在一系列问询点 \(v_{1}, v_{2}, ... ,
v_{k}\) 能寻找到 \(x\) 点.
树上节点数量小于2000
思路:
没有思路, 题解是贺的.
\(key\;observation:\)
对于任意一个根节点 \(u\) ,
其所有子树中, 只能有一颗子树不含查询点,
否则不含查询点的子树的高度相等的点无法排除,只剩一颗子树不含查询点则可以通过容斥确认
\(x\) 点所在子树。
考虑 \(O(n^2)\) 暴力树型 \(DP\) , 枚举每个根节点并保证选取,
接下来要做的就是确定唯一的子树节点。状态转移 \(dp_{u}=\sum\limits_{v\in
son_{u}}dp_{v}+max(cnt_{u}-1,0)\) , 其中 \(cnt_{u}\) 代表子树个数为 1 的 \(u\) 的子节点数量, 最终答案 \(dp_{root}+1\) , \(dp_{root}\) 记得取 \(min\) , 答案最后再取根节点 \(+1\) 。
代码:link
D2
题意同上。
树上节点数量小于2e5
思路:
做完 \(D1\) 再来看, 一眼 换根DP ,
但其实有更优雅的解法(毕竟我也不会换根DP)。
考虑到枚举根节点复杂度过大, 尝试压缩,有两个结论:
1、除了根是否要询问,其余询问的总次数固定。
2、若根节点的的子节点数量 \(>2\) , 则这个根节点不需要询问。
这两个观察是“信仰之跃”式的思维跳跃, 关键是注意到 D1 的子树上查询点的选择其实等价于对于每个以 \(v\) 为根的子树, 要么查找到 \(v\) 节点, 要么在 \(v\) 节点的子树外有查询以确定 \(x\) 点所在的子树, 当根节点的的子节点数量 \(>2\) 时几个节点互相确定, 不用选根节点, 性质二又能推出性质一(换根)。
如果没有根节点的子节点的数量 \(>2\) 原树则为一条链, 答案为 1。
抄完题解还是较难理解……
代码:link
Educational codeforces round 131 (#Div2) 22/7/8
$(1715, rk2820) $
需要复健,怕是废了。 \(ABC\)
都做得很慢, 还发现简单套路题做得真的不多, 慢慢刷吧……
D
题意:由排列 \(a\) 构造出数组 \(b\) , 其中 \(b_{i}= \lfloor\frac{i}{a_{i}}\rfloor\)
,现在已知 \(b\) , 求一个可行的 \(a\) .
思路:
1、要确定每一个 \(b_{i}\) 对应的 \(a_{i}\) 的范围, 我自己用数论分块 + 二分弄出
\(a_{i}\) 的范围,
大佬题解的搞法是找等价条件, 注意不到 \(b_{i}= \lfloor\frac{i}{a_{i}}\rfloor\)
等价于: \[b_{i}\leq\frac{i}{a_{i}}<b_{i}+1\]
又等价于: \[
\lfloor\frac{i}{b_{i}+1}\rfloor+1 \leq a_{i}
\leq\lfloor\frac{i}{b_{i}}\rfloor\]
注意这里的左界的符号变化。
2、此时问题转换为区间选数构成排列,现场我就寄在这里……
简单贪心一下:从 \(1\) 到 \(N\) ,每次加入这个左端点对应的所有区间,
选择右端点最小的先处理, 这样可以给后来的多一点选择空间。
实现:
对每一个左端点建一个 \(vector\) , 存
\(pair\), 第一键值右端点,
第二键值存下标 , 再建一个 \(pair\) 的
\(set\), 循环时把对应 \(vector\) 全压进 \(set\) 里, \(set\) 每次处理一个。
代码:
1 | for(int i=1;i<=N;i++) v[i].clear(); |
注意: 不要在函数内定义你该死的 vector[MAXN].
E
开始赛后补题……
题意:给你两个字符串 \(s, t\),长度为
\(N, M\) , 均小于 5000, 保证 \(N\geq M\) , 问至少多少个操作能将 \(s\) 转换为 \(t\) , 不能则输出 \(-1\) , 一开始有一个光标在 \(s\) 末尾, 操作有五种:前移一位光标;
后移一位光标; 光标置于最前; 光标置于最后; 删除光标前的字母。
思路:很明显光标肯定只会回到最前端一次或不回去, 不会反复横跳,
并可能在中间存在不需修改的部分。
我们可以把 \(s\) 串分为三部分 DP ,
前修改串, 中保留串(不修改), 后修改串。然后开始贺题解: 设
\(f_{i,j,0/1/2}\) 表示处理到 \(s\) 的第 \(i\) 个字母, 并已经和 \(t\) 的前 \(j\) 个字母匹配完成, 0/1/2 分别代表 前/中/后
三部分。
1、在任意时刻前缀与后缀部分都可以删除后/前字母,
其中删除后字母的代价为两次操作(右移+删除),
而删除前字母的代价为一次操作(删除), 转移如下:
\[f_{i,j,0}=min(f_{i,j,0},f_{i-1,j,0}+2)\]
\[f_{i,j,2}=min(f_{i,j,2},f_{i-1,j,2}+1)\]
2、在 \(s_{i}=t_{j}\) 时刻,
可仅仅移动光标完成匹配, 中间部分则直接沿用:
\[f_{i,j,0}=min(f_{i,j,0},f_{i-1,j-1,0}+1)\]
\[f_{i,j,1}=min(f_{i,j,1},f_{i-1,j-1,1})\]
\[f_{i,j,2}=min(f_{i,j,2},f_{i-1,j-1,2}+1)\]
3、任意时刻的匹配都能从处于前面的部分转入处于后面的部分:
\[f_{i,j,2}=min(\{f_{i,j,0},f_{i,j,1},f_{i,j,2}\})\]
\[f_{i,j,1}=min(f_{i,j,0},f_{i,j,1})\]
你可以理解为虽然真实顺序是从后到前跳转, 但我们从前到后正常处理匹配,
最终汇总到 \(f_{i,j,2}\) 中,
这个记得最后更新
4、若存在不回到开头的方案, 其操作数为 \(N-len\) , 其中 \(len\) 为 \(s,t\) 串最长公共前缀的长度,
它要在与回到开头的答案 \((f_{N,M,2}+1)\) 取 \(min\) 。 代码:link
原题卡空间, 还要开滚动数组, 在循环中再设初始值吧……
F
题意:
数轴上三元组 \((i,j,k)\) , 满足 \(i<j<k\;\&\&\;k-i\leq D\)
的为好三元组, 一开始数轴为空, \(D\)
为定值, \(Q\) 个操作, 每次给你一个数
\(\in [1,2e5]\) , 若未加入过就加入,
已加入过就删除, 在线求当前数轴中好三元组的数量。
思路:
简化问题, 考虑加入一个点时它分别作为三元组的 \(i,j,k\) 时的贡献。每个点 \(x\) 的加入会影响 \([max(0,x-D),min(2e5,x+D)]\) 的范围,
我们对每个点 \(p\)
受到来自左边或右边的影响单独计数, 为 \(l_{p},r_{p}\) , 这样当 \(p\) 作为 \(i\) 时的贡献为 \(\frac{1}{2}*r_{p}*(r_{p}-1)\) , 同理 \(p\) 作为 \(k\) 时的贡献为 \(\frac{1}{2}*l_{p}*(l_{p}-1)\) 。
现在考虑当 \(p\)
处于三元组中间时的贡献, 看上去难以下手(我到这儿就想不出来了),
一个切入口是暴力统计
\[\sum\limits_{i=p-D}^{p-1}{[i_{exist}]}*\sum\limits_{k=p+1}^{i+D}{[k_{exist}]}\]
(\(i_{exist}\)表示 \(i\) 点已经在数轴上)这个暴力重复过多,
可以再拆一下贡献, \(\sum\limits_{k=p+1}^{i+D}{[k_{exist}]}\)
就可以拆为
\[\sum\limits_{k=1}^{i+D}{[k_{exist}]}-\sum\limits_{k=1}^{p}{[k_{exist}]}\]
来做一个简单前缀和, 记 \(c[l,r]\) 为
\([l,r]\) 内点的个数,
所以贡献为:
\[\sum\limits_{i=p-D}^{p-1}{([i_{exist}]*c[1,i+D])}-c[p-D,p-1]*c[1,p]\]
前面是动态的所以还是得展开, 我们可以再记 \(v_{i}=c[1,i+D]\) , 最终贡献:
\[\sum\limits_{i=p-D}^{p-1}{([i_{exist}]*v_{i})}-c[p-D,p-1]*c[1,p]\]
剩下的简单了, 线段树维护 \(v, c\) 就行,
之前的 \(l_{p}, r_{p}\) 也可以用 \(c[x-D,x-1],c[x+1,x+D]\) 换掉了, 注意有关
\(0\)
的边界情况还是要特判的……删除同理……
代码: link
其实小细节挺多, 我的实现略繁琐, 用了 \(v1,
v2\) 两个数组来处理 \([i_{exist}]\) , \(v1\) 为 \(v\) , \(v\) 有两次更新, 在单点更新 \(c\) 时把之前 \(v1\) 积累的更新给 \(v2\)
一并加上,向上更新;第二次区间更新考虑单点更新 \(c\) 时对 \([max(1,i-d),2e5]\) 的 \(v1,v2\) 都有影响, 向下更新, 打懒标记什么的,
最后实际询问的是 \(v2\)
贡献。删除的更新顺序与上面相反。此外还要注意数轴长度固定为 \(200000\),与 \(Q,D\) 无关, 记得开 \(long\;long\) ,
这题算一个不错的线段树题。
codeforces round 808 (#Div2) 22/7/16
\((1661\rightarrow1621,
rk2785)\)
两个月来最差的一把。
十九分钟过了\(A,B\) ,
然后罚坐到比赛结束都没能把1600的 \(C\)
写出来, 明明只是一个贪心, 现在是7/21的凌晨1:48, 喝了咖啡睡不着,
起来补题, 最近效率很低, 作息也不稳定,
今天能补到哪里算哪吧……现在学OI只有一个目标……cf上1900,
人生的意义就是这点薯条了, 其他我都不想管……
C
题意:
对于数组 \(a\) 与初始值 \(q\), 按顺序遍历 \(a_{1}\) 到 \(a_{n}\) ,若 \(q
\geq a_{i}\) , 则可以取走 \(a_{i}\) 而不付代价, 否则若选择取走 \(a_{i}\) 则会付出 1 的代价,
问最多能取走几个物品。
思路:
越晚取越好是肯定的, 但太晚取多余的 \(q\) 又会被浪费。
可以推断出不取 \(a_{i}\) 的条件:\(q<a_{i}\) 且 \(q<\sum\limits_{i}^{N}[q<a_{i}]\),
这样保证即使现在不花 \(q\) 来取,
后面总是能花掉的。
代码:link
这题二分也行, 搞笑的是我考场上两个都想过却都认为自己想假了, 试都没试一下。
D
题意:
求一个 \(N\) 位有序数组(每项值域为
\([1,5e5]\) , 从小到大排序)的 \(N-1\) 阶差分数组(最后的一个数字),
不同的是每次求完差分数组都要对其从小到大排序。
思路:
以为是推式子题, 啥也没推出来。 很有趣的一道题,
看到差分数组想到痛苦的回忆, 再看一眼题解 "对于值域为 \(N\) 的有序数组差分后最多产生 \(\sqrt{N}\) 个不同的数" , 逐渐痛苦起来了,
又注意到 \(0\) 对差分无贡献,
这样本题就暴力可解了, 复杂度 \(O(N\sqrt{N})\)。
代码: 上 \(map\) 和 \(auto\)
1
2
3
4
5
6
7
8
9
10
11N=read(); mp.clear();
for(int i=1;i<=N;i++) ar[i]=read(), mp[ar[i]]++;
for(int i=1;i<N;i++){
for(auto it=mp.begin();it!=mp.end();it++){
if(it->second>1) mp2[0]+=(it->second-1);
auto nxt=it; nxt++;
if(nxt!=mp.end()) mp2[nxt->first - it->first]++;
}
mp=mp2; mp2.clear();
}
cout << mp.begin()->first << endl;
这题在 codechef 上有一个困难版本,
应该只能用 \(n log n\) 做法了, 给个link自己看……
E
题意:
给你错误的求最小生成树的 \(Prim\)
代码(贪心部分只寻找了当前点连接的最小边, 生成从每个点出发的 DFS 搜索树),
给你图, 保证有唯一正确的最小生成树,
问从每个节点运行错误代码得到的是不是最小生成树。
思路:
先把正确的最小生成树求出来, 观察图像:
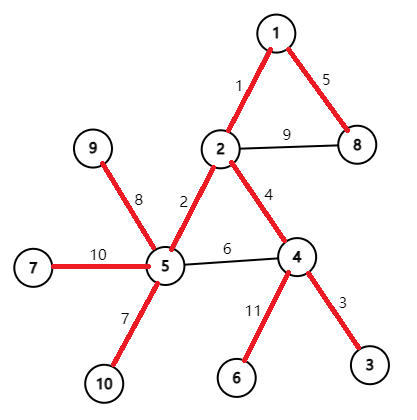
随手做的……红线为 MST 边, 在这个例子中, 从 1, 2, 8
节点开始的错误算法会选择 4-5 边导致最后生成错误的树。
我们设没选的边类型分为两种, 返祖边与横叉边。让我们从 8 号节点开始举例,
按照错误的算法, 先连 8-1, 再连 1-2, 此时 2-8 为一条返祖边, 连接选择过的
8 号节点, 所以返祖边不会被选择。继续模拟, 连 2-5, 此时按照错误算法应连接
5-4,5-4 便为一条横叉边, 其两个端点位于 2 号节点的不同子树中, 因为 4
号节点未被选择过, 按照 DFS 的顺序, 正确的 2-4 边不可能被选择, 要么选 5-4
边, 要么选择另一条(如果存在) x-4 的横叉边, 所以横叉边不能存在。
问题转化为计算以每个点为根时是否存在横叉边, 考虑每条非 MST 上的边 u-v,
若 lca(u,v)!=u/v, 则 u, v 子树外的点全部不合法(先到 u/v, 再根据 DFS 走
u-v 边), 若 lca(u,v)=u/v, 则从 u 到 v 链上的点的子树全部不合法(除u,
v两点), 如图:
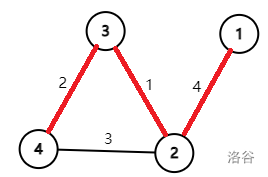
从 3 号节点开始走不合法。
最后用树上差分的方式给不合法部分打上标记, 统计输出。
具体讲一下这里的差分策略, 对于 lca!=u/v 情况, 在 u, v, lca 上打上 +1,
+1, -1 标记; 对于 lca=u/v 情况, 在 \(u\;(dep_{u} \geq dep_{v})\) 上及满足 \(fa[t][0]=v\) 的 t 点上打上 +1, -1 标记,
最后 dfs 统计的时候每个点的值等于该点到根节点链上的差分值之和, 若值为 0
则说明该点合法。
代码:link
事实上我可以边读边边跑 \(kruskal\)
的……就不用 \(f1\), \(f2\) 了。
codeforces round 809 (#Div2) 22/7/18
\((1621\rightarrow1694,
rk733)\)
D1 糊过的, 现在自己代码看不懂了......
D2
题意:
给定数组 \(a\) , 长度为 \(N\), 定义 \(a\) 的价值为 \[\underset{1\leq i \leq
N}{max}(\lfloor\frac{a_{i}}{p_{i}}\rfloor)-\underset{1\leq i \leq
N}{min}(\lfloor\frac{a_{i}}{p_{i}}\rfloor)\] 其中 \(1 \leq p_{i} \leq k\) , 给定 \(k\) , 求最小的价值, \(1 \leq N, a_{i}, k \leq 1e5\), 空间 \(64M\) 。
思路:
有一点整除分块思想。
D1还可以简单枚举 \(\lfloor
\frac{a_{i}}{p_{i}}\rfloor\) , 但现在不行了, 算一下当 \(k\) 足够大时, 设 \(b_{i}=\lfloor \frac{a_{i}}{p_{i}}\rfloor\)
最多有 \(2 \sqrt a_{i}-1\) 种取值,
\(b_{i}\) 不可能全部存下来,
尝试在双指针扫的同时动态求 \(b_{i}\),
用 \(cnt_{i}\) 表示区间内一个 \(i(a_{i})\) 对应的合法的 \(b_{i}\) 数量, 当 \(tot=\sum[cnt_{i}\geq 1]=N\)
时更新最小区间长度。 在具体实现上, 由于 \(p_{i}\) 从小到大, \(b_{i}\) 从大到小, 从可能的最大值开始双指针,
分开给左右指针开 \(vector\) ,
处理一个位置后清空它的内存。
代码:
1 | N=read(); K=read(); M=0; |
有一些要注意的点:
1、在这里 \(p_{i} \leq a_{i}\) ,
因为我们不需要 \(p_{i} > a_{i}\) 时
\(b_{i}=0\) 的情况,
这样会在整除分块时越界, 而且所有 \(b_{i}=0\) 的情况都可以用 \(b_{i}=1\) 替代。
2、循环改成 $ for(auto i:ql[l])$ 会简单不少……现在只是让你看一下挂 \(i\) 的好处。
3、\(vector\) 释放内存用
vector
E
题意:
无向图,给 \(n\) 个点, \(m\) 条边并标号, \(q\) 个询问, 每次询问一个最小的 \(k\) , 满足标号在 \([l,r]\) 之间的点仅使用前 \(k\) 条边便两两联通, \(n \leq 1e5, \;m, q \leq 2e5\)。
思路:
看到 \(q \leq 2e5\) ,思考可复用性,
考虑到记 \(c_{i}\) 为 \(i\) 点到 \(i+1\) 点经过的边的最大编号, 建线段树,
每次静态查询 \(c_{l}\) 到 \(c_{r}\) 之间的最大值, 问题转化为求出 \(c_{i}\)。
如果你知道 \(kruskal\)重构树,
那么你赢麻了,因为你知道:
原图中两个点之间的所有简单路径上最大边权的最小值 =
最小生成树上两个点之间的简单路径上的最大值 = \(Kruskal\)重构树上两点之间的 LCA
的权值。
但我输麻了, 我只会最小生成树, 所以我证明一下结论的前半部分:
按照 \(kruskal\) 算法的加边顺序,
如果有一条边 u-v 不在 MST 上,
说明先前的贪心已经使用了边权更小的边连接上了 u-v, 所以结论成立。
代码:link
简单线段树 + LCA + kruskal......
Educational codeforces round 132 (#Div2) 22/7/21
$(1694, rk3029) $
又寄回来了, 我都不想写这个, 搞得很尴尬, 这场是最寄的, C >> D, 而我
D 又因为一个 max/min 没加写挂了, 就下了大分, 又成为 1600 守门员......
因为博客太长, 后台的高亮显示已经出问题了, 决定每 10 场开一篇博客,
然后总体记录总结。
C
题意:给你括号串, 问号为通配符, 保证存在合法, 问是否唯一。
思路:注意到这是个贪心就好写了, 因为保证存在合法, 可以先把所有的 \((\) 填掉, 再填 \()\), 除此之外最有可能合法的便是交换最后一个
\((\) 与第一个 \()\) , 只要检查一下这个就可以了。
代码:link
E
D是裸的线段树就不放了……
题意:给一颗树, 顶点有值($ 1a_{i} ^{30}$),
为了满足树上所有简单路径的异或和不为零,
你需要至少修改几个顶点(可改为任意正整数)?顶点数 \(\leq 2e5\)。
思路:
没有思路, 贺题解, 启发式合并。
一开始没有注意到可修改为任意正整数, 想了个寂寞。
注意到如果一条简单路径不合法, 改变 lca 处一定不劣于改变其他处,
因为改变的值可以任意构造, 改变 lca
可以保证切断所有子树对其他部分的影响。这样, 记 \(dis_{i}\) 为 \(i\) 点到根节点的异或和, 所以 \(u\rightarrow v\) 的简单路径和为 $
dis_{u}dis_{v} a_{lca}$ , 根据异或的性质, 对于每个满足 \(x=lca(u,v)\) 的 \(x\) 点, 若 \(dis_{u} \bigoplus dis_{v}=a_{x}\)
则必须要修改 \(x\) 点。
具体实现方面:dsu on tree, 每一个节点开一个 \(set\) 记录这个节点子树的(含自身) \(dis\), 若一个节点被改变, 则其 \(set\) 为空(切断连接), \(dfs\) 一个节点的时候把它的重儿子直接换上来,
对于轻儿子, 先查询再尝试合并。
代码:(省略了求 \(dis\) 的过程)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void dfs2(int x, int f)
{
if(son[x]) dfs2(son[x],x), swap(s[x],s[son[x]]);
int tag=0; //choose(delete) or not
if(s[x].find(dis[x]^ar[x])!=s[x].end()) tag=1; // detect dis[x] illegal to insert
s[x].insert(dis[x]); //insert
for(int i=head[x];i;i=e[i].nxt)
{
int y=e[i].to;
if(y==f||y==son[x]) continue;
dfs2(y,x);
for(auto i:s[y]) if(s[x].find(ar[x]^i)!=s[x].end()) tag=1; //find s[son[x]] ^ s[y] = ar[x]
for(auto i:s[y]) s[x].insert(i); //combine
}
if(tag) s[x].clear(), ans++;
}
再分享一个 \(\color{red}{wsyear}\) 的代码,
惊为天人的简洁。
codeforces round 810 (#Div2) 22/7/24
\((1639\rightarrow1629,
rk1814)\)
已经无处可掉了, 手速场没手速, 罚时多 D 又不会……
D
题意:
下 \(N\) 天雨, 每天下雨在数轴上 \(x_{i}\) 处, 强度为 \(p_{i}\), 位置 \(x_{j}\) 会受到 \(max(0,p_{i}-|x_{i}-x_{j}|)\) 的降雨,
当任意时间任意位置降雨量大于 \(M\)
时发生洪水, 问对于每一天, 取消当日降雨量会不会导致洪水。
思路:见等差数列想差分, 下面是一个 \(x_{i}=5\) , \(p_{i}=4\) 的二阶差分表格
| 0 | 1 | 2 | 3 | 4 | 3 | 2 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | 0 |
| 0 | 1 | 0 | 0 | 0 | -2 | 0 | 0 | 0 | 1 |
可以做二阶前缀和回到原数组, 现在看去掉一段 \((x_{i},p_{i})\) 的降雨对在总降雨量为 \(val\) 的 \(x_{j}\) 点有什么影响:
1、设 \(x_{j}\geq x_{i}\) ,此时 \(x_{j}\) 点降雨量为: \[val-(p_{i}-(x_{j}-x_{i})) \iff
val-p_{i}+x_{j}-x_{i}\]
所以若不发生洪水需要满足: \[val+x_{j}-M \leq
p_{i}+x_{i}\] 2、设 \(x_{j} <
x_{i}\) , 同理有 \(val-M-x_{j} \leq
p_{i}-x_{i}\)
接下来我们只需求解最大的 \(val+x_{j}-M\) 与 \(val-M-x_{j}\) 即可。 具体来说, 我们不用关心
\(x_{j}\) 和 \(x_{i}\) 的大小关系,
因为原式计算是带绝对值的, 不影响结果。又因为若 \(val \leq M\) , 则当点去掉降雨无影响,
需要省去。
代码: link
本题用 \(vector\) 就行了,
当然若你用扫描线/差分+线段树写 div2D, 也是可以的……
E
数位DP, 咕
codeTON Round 2 (#Div1+2) 22/7/31
\((1629\rightarrow1651,
rk2075)\)
应该是打的第一场 div1+2,因为 D 的一个构造想不出来罚坐近 2h, 又成了 ABC
战神……
D
题意:
给你一个数组 \(b\) , 长度为 \(m\) , 在此基础上生成 \(n\) 个数组, \(c_{1}...c_{n}\) , 一开始的 \(c_{i}=b\) , 有一个特殊数组 \(c_{k}\) ; 生成数组的规则是:
1、选择 \(i, j\), 满足 \(2 \leq i < j \leq m-1\) \[t \neq k, c_{t}[i-1]+1, c_{t}[i]-1, c_{t}[j]-1,
c_{t}[j+1]+1\] 2、选择 \(i, j\),
满足 \(2 \leq i < j \leq m-2\) \[t = k, c_{t}[i-1]+1, c_{t}[i]-1, c_{t}[j]-1,
c_{t}[j+2]+1\] 每个 \(c_{i}\)
至少完成一次上述操作, 给你最后的 \(c_{1}...c_{n}\) , 问你 \(k\) , 以及 \(c_{k}\) 完成了多少次操作?
思路:
本题看似唬人, 实则唬人, 设 \(pre\)
为一个 \(c_{i}\) 的前缀和数组:
对于操作一, \(pre[i-1]+1,
pre[j]-1\)
对于操作二, \(pre[i-1]+1, pre[j]-1,
pre[j+1]-1\)
于是做完了。
代码:link
E
题意:
有向无环图(\(n,m\leq1000\)),
每个节点有正值, 恰好有一个没有出边的节点, 每秒钟每个节点的值 -1 ,
并将所通向的节点的值 +1 , 找到所有的节点的值为 0 的第一个时刻, 答案模
998244353 输出。
思路:
类似拓扑排序, 但要注意在节点变为 0 后是有重新获值的可能性的,
比如说本身为 0 , 但几代前的父节点有值, 考虑起来十分复杂, 于是注意到
\(n \leq 1000\) , 只要暴力完成前 \(n\) 轮, 再拓扑最后一轮累加,
就可以了。
代码:link
F
SG函数, 咕咕咕咕咕
Educational codeforces round 133 (#Div2) 22/8/4
\((1651\rightarrow1749,
rk476)\)
坚持不看榜人 70 mins 才出 C, 以为又要寄了, 但这把 CD 都难……, ABC
战神反而能上分……
D
题意:
给你 \(n, k\), 从数轴原点开始, 第 \(i\) 次可以跳 \((i+k-1)\) 的倍数步(不可以跳 0 步), 问你跳到
\([1,n]\) 格各有多少种方案。 \(n,k \leq 2e5\), 方案数模 998244353。
思路:
完全背包问题稍微改了改, 最多有 \(m\)
种物品(步数与其倍数), 满足 \((2* k+m-1)* m
\leq 2* n\) (等差数列求和), 注意每种"物品"至少要取一种,
可以从之前的转移……, 复杂度 \(O(n\sqrt
n)\)。
代码:
1
2
3
4
5
6
7
8
9
10f[0]=1;
for(int i=1;(2*K+i-1)*i<=2*N;i++){
int t=i+K-1;
for(int j=t;j<=N;j++)
f[j]=(f[j]+f[j-t])%p;
for(int j=N;j>=t;j--) f[j]=f[j-t];
for(int j=t-1;j>=0;j--) f[j]=0;
for(int j=t;j<=N;j++) ans[j]=(ans[j]+f[j])%p;
}
for(int i=1;i<=N;i++) cout << ans[i] << " "; cout << endl;
E
题意:
给你 \(2^n\) 长的数组 \(a\) , \(q\) 组操作, 每次操作给一个 \(k\) , 数组从 \(1\) 遍历到 \(2^n-2^k\) , 在没有交换过的前提下交换 \(a_{i}\) 与 \(a_{i+2^k}\) ,
每次操作结束后问你最大字串和(包括空字串)。 \(n
\leq 18, q \leq 2e5\)。
思路:
手玩一组样例, 设 \(k=1\) , \(a_{1}\) 换 \(a_{3}\), \(a_{2}\) 换 \(a_{4}\), \(a_{5}\) 换 \(a_{7}\), \(a_{6}\) 换 \(a_{8}\dots\)。
我们想到了要找寻一种性质来总体描绘一次操作中的所有交换。因为一次操作内部以
\(2^k\) 为单位, 想到下标的二进制表示,
若下标从 \(0\) 开始, \(0, 1, 10, 11, 100, 101, 110, 111\) ,
不难看出每次交换其实是让下标异或 \(2k\)。
如何维护最大字串和? 考虑线段树, \(2^n\) 的长度, 一定是漂亮的满二叉树,
每次给的 \(k\) 相当于在线段树的倒数
\(k+1\)
层交换两个子树。若暴力做这个交换, 每次自底向上维护, 则有 \(O(4^n)\) 的复杂度, 肯定是寄的。
题解的方法优雅又暴力, 把节点的所有版本在建树时就保存下来,
最后操作的时候直接异或输出异或输出就可以了。 对于一个长度为 \(2^m\) 的线段树节点 \(v\) , 有 \(2^m\) 种状态, 对应当前 \(\sum2^k=[1,2^m]\) , 其左右儿子同理便有
\(2^{m-1}\) 种状态, 我们从 \(0\) 到 \(2^m-1\) 枚举 \(i\) ( \(0\) 为初始态, \(2^{m}-1\) 为 \(k\) 取遍 \(0,1,2,\dots, m-1\) 的“最乱状态”),
有如下转移(设 \(t(v,x)\) 为 \(v\) 节点的第 \(x\) 种状态):
1、 \(i < 2^{m-1},
\;t(v,i)=combine(\;t(ln,i),\;t(rn,i)\;)\)
2、 \(i \geq 2^{m-1},
\;t(v,i)=combine(\;t(rn,i-(2^{m-1})),
\;t(ln,i-(2^{m-1}))\;)\)
这个 \(combine\) 就写成结构体构造函数,
维护一些最大前缀和, 后缀和, 字串和, 总值这样的东西……
因为 \(i \in [0,2^{m}-1]\) , 所以 \(i \geq 2^{m-1}\) 就代表出现了 \(k=m-1\) 换掉了 \(v\) 的左右儿子。
这种做法复杂度全在建版本上, 版本有 \(n2^n\) 个, 查询为 \(O(1)\) , 复杂度为 \(O(n2^n)\) .
代码:
1 | struct node{ |
别忘了你的 resize !
F
斯特林数与下降幂……咕咕
Codeforces round 812 (#Div2) 22/8/6
\((1749\rightarrow1735,
rk1538)\)
ABC 战神, 勇于跳 D 开 E 不跟榜还观察不出来 D 性质的傻子,
罚时与罚坐大师今天又掉分了……(不是三个人, 是一个人)
D(交互)
题意:
\(2^n\)个人打比赛, 赢者晋级输者淘汰,
最多 \(\lceil\frac{1}{3}*
2^{n+1}\rceil\) 次询问任意两个人的胜利次数大小关系,
问谁是最后的赢家。
思路:
数学很好的你一眼就注意到 \(\lceil\frac{1}{3}* 2^{n+1}\rceil=\lceil\frac{2}{3}*
2^{n}\rceil\) (废话),
又注意到了 \(2*\sum\limits_{i=1}^{\infty}{\frac{1}{4^n}}=\frac{2}{3}\),
一下子就发现了只要每四人一组, 用两次询问得到四人中的赢家,
向上递归便能轻松解题。
代码:link
E
题意:
给一个矩阵, 每次可以选一个 \(k\)
并交换所有的 \(a[i][k], a[k][i]\),
问可能得到的最小字典序的矩阵。
思路:
显然对于矩阵上的一格 \(a[i][j]\),
有唯一对应的 \(a[j][i]\) , 选择 \(i, j\) 均可完成交换, 若交换, 则两者选其一;
若不交换, 则两者均选或均不选。
考虑种类并查集, 开两倍的并查集, 注意当两者关系已确定后不再更新。
代码:link
不会卡常……警示后人, 用 ‘' 换掉你的 'endl'。
F
FMT……, 要咕一辈子了
Codeforces round 813 (#Div2) 22/8/13
\((1735\rightarrow1729,
rk1599)\)
这场 135 mins, ABC 做完只用了 20mins 左右, 我以为 D 稳了,
先罚坐了一个小时, 静下心来想和之前的 809E 很像,
都有一个点两两联通的无向图, 也可以按照顺序拆成链, 遂码之,
最后样例测过了, 我交上去, 以为还有一分钟,
但我电脑卡延迟了……实际上比赛已经结束了, 现在是 8/14, 1:28am,
我紧张的等待 system test 结束后想再交一发……我既期冀着打破 ABC 的魔咒,
又有一点不希望自己能成功……看别人写的都是二分, 而我用上了线段树……
交了一发, D 错了, 去睡觉了……
D
题意:
给你一个数组 \(a\) , 可以更改其中的
\(k\) 个数, 图上两点 \(i, j(i<j)\) 的边权为 \(min([a_{i}\dots a_{j}])\) ,
问你能得到的最大树的直径为多少。
思路:
注意到树的直径一定从相邻两点的距离中选出, 假设非相邻两点的距离是直径,
两点之间的最短路只会从 \(min(a_{i},a_{j}), 2*
min([a_{1}\dots a_{n}])\) 中取得, 可以观察到走三步以上没有意义,
走两步最小值的构造方法是:看 \(a\)
中最小值在起点( \(a_{i}\)
)的左边或右边, 然后先去左边的 \(a_{1}\)(或右边的 \(a_{n}\) )再回到 \(a_{j}\) 即可。这样看来,
最长的最短路一定在相邻两点间取得。
从 \(a_{i}\) 到 \(a_{i+1}\) 有三种走法:直接走 i--j, 走 i--1,
1--i+1, 走 i--n, n--i+1, 第二、三种走法要求我们预处理出前缀,
后缀最小值。
现在便有了一个二分做法:二分出 mid , 将前缀后缀 \(2* a_{i} \leq mid\) 的值修改,
看修改的数目与 \(k\) 的关系, 复杂度
\(O(n log n)\)
代码:link
E1
题意:
给你 \(l, r\) , 找出满足 \(lcm(i,j,k) \geq i+j+k\) 的三元组 \((i,j,k)\) 数目, 其中 \(l \leq i<j<k \leq r\), \(l,r \leq 2e5\) 最多五组数据。
思路:
正难则反, 思考计算 \(lcm(i,j,k) <
i+j+k\) 的三元组数目, 注意到 \(lcm(i,j,k)\) 为 \(k\) 的倍数, 因为 \(2* k \leq i+j+k < 3* k\) ,
所以所有不合法的三元组必须满足以下条件:
\[lcm(i,j,k)=k\;\;or\;\;lcm(i,j,k)=2k,
i+j>k\]
只要枚举 \(k\) 的约数, \(2k\) 的约数即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17ll sum=(ll)(r-l+1)*(r-l)*(r-l-1)/6;
int num=0;
for(int i=l+2;i<=r;i++){
for(auto x: fac[2*i]){ //k = i
if(x<=l) continue; //j > l
if(i%x&&2*x<=i) continue; // continue if x is the factor of 2k but x+y<k (2k part)
if(x>=i) break; //x = j < k
for(auto y: fac[2*i]){ //y = i < j = x <k
if(y<l) continue;// i >= l
if(y>=x) break; //i < j
if(i%x||i%y) // x/y is factor of 2k (2k part)
num+= (x+y>i); //can they?
else num++; //x/y is factor of k
}
}
}
cout << sum-num << endl;
E2
题意同上, 最多可能有 2e5 组数据。
思路:E1都是贺的我 E2 有屁思路
考虑离线下来做, 同上, 从小到大枚举 \(k\) , 将 \((i,j,k)\) 中所有有贡献的 \(i\) 及其贡献(固定 \(i,k\) 后的三元组数目)用树状数组单点修改,
每次枚举完 \(k\) 后查看是否有 \(r=k\) 的询问, 其答案便为树状数组上 \(i\) 到 \(k\) 的区间求和。
代码:link
F
长链剖分, 咕。
Codeforces round 814 (#Div2) 22/8/16
\((1729\rightarrow1774,
rk501)\)
ABC 战神糊出来了 D1 , 上了小分。
D2
题意:
给你大小为 \(N\) 的数组 \(a\) , 每次可以选择 \(l, r, x\) 使得 \([l,r]\) 范围内的数全部异或 \(x\) , 并耗费 \(\lceil \frac{r-l+1}{2}\rceil\) 的代价, 问将
\(a\) 数组全部置零的最小代价。\(N \leq 2e5\) 。
思路:
因为有上取整的要求, 一次操作范围为 2 的数字是最赚的,
范围再扩大则没有必要, 原先的 D1, \(N\)
的范围在 \(5000\) 以内, 可以暴力二维
\(DP\) ,
原先有一个简单的置零方法就是一个一个置零, 代价为 \(N\), 我们每两个两个操作就可能省下一个代价,
我的 D1 做法是设 \(f_{i,j}\) 为考虑省下
\(i\) 处代价, 从头一直处理到 \(j\) 处所省下的代价。
\[f_{i,j}=max(f_{1,i-1},f_{2,i-1},...,f_{i-1,i-1})+[a_{i}
\oplus a_{i+1} \oplus ... \oplus a_{j} == 0]\]
最后取 \(N-max(f_{1,N},f_{2,N},...,f_{N,N})\)
为答案, 有点玄学, 我也不知道怎么过的题, 复杂度 \(O(n^2)\) 。
事实上我们可以直接设 \(f_{i}\) 为将
\(1...i\) 所有数置零付出的最小代价,
要么我们操作长度为 1 的数组一次, 要么我们一直操作长度为 2
的数组直到某段区间的异或和为零。
\[f_{i}=min(f_{i-1}+1, \underset
{a_{j+1}\oplus a_{j+2} \oplus...\oplus
a_{i}=0}{min}(f_{j}+i-j-1))\] 复杂度也是 \(O(n^2)\) , 但应该有了些优化空间,
比如把最小的 \(f_{j}-j\) 存入 \(map\) 中, 事实上, 我们还可以设 \(xors_{i}=a_{1} \oplus a_{2} \oplus ...\oplus
a_{i}\) , 那么有 \(a_{j+1}\oplus
a_{j+2} \oplus...\oplus a_{i}=0 \Longleftrightarrow
xors_{j}=xors_{i}\) 这样一个小性质。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15N=read();
for(int i=1;i<=N;i++){
ar[i]=read(); f[i]=inf;
xors[i]=xors[i-1]^ar[i];
}
MII mp;
mp[0]=0; //记录前缀和i所对应的最小 f[j]-j
for(int i=1;i<=N;i++){
if(!ar[i]) f[i]=min(f[i], f[i-1]);
else f[i]=min(f[i],f[i-1]+1);
if(mp.find(xors[i])!=mp.end())
f[i]=min(f[i],mp[xors[i]]+i-1);
mp[xors[i]]=min(mp[xors[i]],f[i]-i);
}
cout << f[N] << endl;
E
题意:
\(k\) 种字符, 每种 \(a_{1}, a_{2},...,a_{k}\) 个,
问是否能用它组成一个字符串 \(s\) ,
使得:字符串中的每一段连续相同字母个数重新组合后是斐波那契数列的前几项。
思路:
显然若 \(\sum a_{i}\)
不等于斐波那契数列的某个前缀和时可以直接判定不存在。先处理出 \(fib[i]\) , 在用 \(map\) 处理出 \(fib[i]\) 的前缀和, 键值设为 \(i\) , 到 90 项就够了。
然后我们知道了最终要构建的斐波那契数列的项数 \(M\) , 考虑贪心的从高项往低项填充,
可以拉个优先队列实现, 又因为相邻两项字符不能相同,
每次填完后剩下的字符数量隔一轮再加回去。
代码:link
F
22/10/23, 应 \(\color{black}{\tt{c}}\color{red}{\tt{hengchunhao}}\)
推荐来补题, \(\color{black}{\tt{c}}\color{red}{\tt{hengchunhao}}\)
大队长直言道, 1600的诈骗题不会补, \(\color{blue}{\tt{frankly6}}\)
怕是连面子都不要了。
题意:
一个循环数组(\(a_{n}\)
后面接 \(a_{1}\)), 自选一个位置 \(s\) 开始跳 \(n\) 步, 步长 \(k
< n\) , 每次把那个位置上的数加入到 "有用值" 中去。 有 \(Q\) 次单点修改, \(a_{p}=v\) , 修改不独立, 问这 \(Q+1\) 次的 \(Q+1\) 个最大有用值。
\(n,Q \leq 2e5, a_{i} \leq 1e9\)
思路:
只会朴素做法……对 \(n\) 的所有不等于
\(n\) 的约数 \(d\) 作为步长, 枚举 \(j \in [0,d-1]\) 作为起始点, 求 \(f(d,j)=d* \sum\limits_{i \equiv
j\;mod\;d}{a_{i}}\) , 再求出最大的 \(f\) , 单次的复杂度应该是 \(O(n* d(n))\) 的。
可以手玩小样例来优化, 设 \(n=12\),
步长 \(k=2,3,6\)
:
1.\(k=2, ans=2 *
max(a_{1}+a_{3}+a_{5}+a_{7}+a_{9}+a_{11},a_{2}+a_{4}+a_{6}+a_{8}+a_{10}+a_{12})\)
2.\(k=3, ans=3 *
max(a_{1}+a_{4}+a_{7}+a_{10},a_{2}+a_{5}+a_{8}+a_{11},a_{3}+a_{6}+a_{9}+a_{12})\)
3.\(k=6, ans=6 *
max(a_{1}+a_{7},a_{2}+a_{8},a_{3}+a_{9},a_{4}+a_{10},a_{5}+a_{11},a_{6}+a_{12})\)
可以看出来 \(k=6\) 一定优于 \(k=2, k=3\) 的答案, 因此若 \(k_{1}|k_{2}\) , 则 \(k_{1}\) 不需要额外求解, 只有当 \(k\) 满足 \(\frac{n}{k}\) 为质数时, 才要求解 \(k\) , 否则 \(\frac{n}{k}\) 可以拆出一个因子安在 \(k\) 身上,
我们只要考虑所有环长(\(\frac{n}{k}\))为质数的环即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29T=read();
while(T--){
N=read(); Q=read();
for(int i=1;i<=N;i++) ar[i]=read();
int tmp=N; cnt=0;
for(int i=2;i<=tmp;i++){
if(tmp%i==0){
d[++cnt]=N/i; // N/d = N/(N/i) = i = PRIME!
while(tmp%i==0) tmp/=i;
}
}
multiset<int> s;
for(int i=1;i<=cnt;i++){
for(int j=0;j<=d[i]-1;j++) f[j][i]=0; // f[j][i] = f(cnt[i],j), cnt[i] is the length of a step.
for(int j=1;j<=N;j++) f[j%d[i]][i]+=ar[j]; //congruence modulo and solve
for(int j=0;j<=d[i]-1;j++) s.insert(d[i]*f[j][i]);
}
cout << *s.rbegin() << '\n'; //rbegin() = end()-1
while(Q--){
int p=read(), x=read();
for(int i=1;i<=cnt;i++){
s.erase(s.find(d[i]*f[p%d[i]][i])); // must use s.find() or it will delete all elements
f[p%d[i]][i]+=x-ar[p];
s.insert(d[i]*f[p%d[i]][i]);
}
cout << *s.rbegin() << '\n';
ar[p]=x;
}
}
Codeforces round 816 (#Div2) 22/8/20
\((1774\rightarrow1764,
rk1256)\)
可能会 D , 但 WA on pretest 4 三发, 遂摆之。
D
题意:
给你长度为 \(N\) 的数组 \(a\) , \(Q\) 个约束条件, 每个约束条件 \((i,j,x)\) 表示 \(a_{i}|a_{j}=x\) , 要你构造一个满足 \(Q\) 个约束条件的字典序最小的数组, \(a_{i} < 2^{30}\)。
思路:
按位把询问的 \(x\) 拆开来, 若 \(x\) 的某一位为零则 \(a, b\) 的对应位全为零, 若 \(x\) 的某一位为一则 \(a, b\) 的对应位至少有一个一。若 \(a=b\) 则那个数字对应 \(x\) 。我们可以先初始化 \(a\) 的每一位为 \(2^{30}-1\) (所有位都为 1 ), 用 vector
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26N=read(); Q=read();
for(int i=1;i<=N;i++) ar[i]=(1<<30)-1;
for(int i=1;i<=Q;i++){
int a=read(), b=read(), val=read();
if(a==b) {ar[a]=val; vis[a]=1; continue;}
for(int k=29;k>=0;k--){
if((val>>k)&1) continue;
if((ar[a]>>k)&1) ar[a]^=(1<<k);
if((ar[b]>>k)&1) ar[b]^=(1<<k);
}
v[a].push_back({b,val});
v[b].push_back({a,val});
}
for(int i=1;i<=N;i++){
if(vis[i]) continue;
for(int j=29;j>=0;j--){
if(!((ar[i]>>j)&1)) continue;
bool tag=1;
for(auto k:v[i]){
int b=k.first, val=k.second;
if(((val>>j)&1)&&!((ar[b]>>j)&1)) {tag=0; break;}
}
if(tag) ar[i]^=(1<<j);
}
}
for(int i=1;i<=N;i++) cout << ar[i] << " "; cout << endl;
E
(于22/11/2日补题……) 斜率优化DP
题意:
有 \(n\) 座城市, 城市间有 \(m\) 条双向道路, 通过第 \(i\) 条道路需要花费 \(w_{i}\) 时间,
两两城市(u,v)之间还可以坐飞机来通行, 花费为 \((u-v)^2\) , 你最多可以做 \(k\) 次飞机, 问 \(1\)
号城市到所有城市的最短时间为多少。
\(n, m \leq 1e5, k \leq 20, w_{i} \leq
1e9\)
思路:
\(dijkstra\) 是肯定要做的, 看到 \(k\) 这么小, 可以想到分层图。
设 \(f[i][k]\) 表示乘坐 \(\leq k\) 次航班从 \(1\) 点到 \(i\) 点且最后一次航班直接到达 \(i\) 点的最短时间, \(dis[i][k]\) 表示乘坐 \(\leq k\) 次航班从 \(1\) 点到 \(i\) 点的最短时间。我们先跑一遍 \(dijkstra\) 求出 \(dis[i][0]\) , 接下来考虑转移, 有:
\[f[i][k]=min\{dis[j][k-1]+(i-j)^2\}, j\in
[1,n]\]
这个复杂度是 \(O(n^2)\) 的,
我们拆一下式子:
\[f[i][k]=dis[j][k-1]+i^2+j^2-2*i*j\]
\[\underline{dis[ j ][ k-1 ] + j^2}_y =
\underline{2*i}_k * \underline{j}_x + \underline{f[ i ][ k ] -
i^2}_b\]
一开始看到平方贡献你就能想到斜率优化了, 现在是个典型的斜率优化式子,
控制枚举顺序, 我们可以让 \(k,x\) 单增,
因为 \(b\) 要最小, 维护下凸壳,
于是我们可以 \(O(n)\) 更新所有的 \(f[i][k]\) , 然后我们再拿着 \(f[i][k]\) 跑 \(dijkstra\) 更新 \(dis[i][k]\) , 重复 \(k\) 次就行了, 复杂度 \(O(kn \;log\;n)\)。
代码:link
F
咕咕, 咕咕咕!!
Educational codeforces round 134 (#Div2) 22/8/27
\((1764\rightarrow1650,
rk4729)\)
大寄特寄, 只会 AB。一个暑假, 除了心态进步, 其余都不曾改变, 上个 edu
场涨的分全掉回来了,
现在凌晨整个人非常清醒......清醒着沉沦......差不多吧。
D
题意:
给你两个数组 \(a, b\) , 你要调整
\(b\) 数组的顺序, 使得构造出来的 \(c\) 数组(\(c_{i}=a_{i}\oplus b_{i}\)) 与起来的和最大
(\(d=c_{1} \&c_{2} \&
...\&c_{N}\) 最大)
思路:
显然要从高往低做, 要想 \(d\)
的二进制中某一位为 \(1\) , 就要判断
\(a\) 中 \(1\) 的个数是否等于 \(b\) 中 \(0\) 的个数, 这样我们能把数组拆成 "a0b1" 和
"a1b0" 两部分, 接下来在两部分内分别递归向下检查就行了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41T=read();
while(T--){
vector<int> a, b, ord;
vector<pair<vector<int>, vector<int>>> t;
N=read();
for(int i=1;i<=N;i++) a.push_back(read());
for(int i=1;i<=N;i++) b.push_back(read());
for(int i=0;i<N;i++) ord.push_back(i); //equals to "iota(ord.begin(), ord.end(), 0);" (c++11)
t.emplace_back(ord,ord);
int ans=0;
for(int i=29;i>=0;i--){
bool tag=0;
for(auto tmp:t){
auto va=tmp.first, vb=tmp.second;
int cnta=0, cntb=0;
for(auto x:va) if(a[x]>>i&1) cnta++;
for(auto y:vb) if(b[y]>>i&1) cntb++;
if(cnta+cntb!=va.size()) {tag=1; break;}
}
if(tag) continue;
ans |= 1<<i;
vector<pair<vector<int>, vector<int>>> t2;
for(auto tmp:t){
auto va=tmp.first, vb=tmp.second;
vector<int> a1, a0, b1, b0;
for(auto x:va){
if(a[x]>>i&1) a1.push_back(x);
else a0.push_back(x);
}
for(auto y:vb){
if(b[y]>>i&1) b1.push_back(y);
else b0.push_back(y);
}
if(a0.size()) t2.emplace_back(a0,b1);
if(a1.size()) t2.emplace_back(a1,b0);
}
swap(t,t2);
}
cout << ans << endl;
}
return (0-0);
E
持久化 KMP , 咕
F
题意:太长机翻
思路:
二分图中, 最大匹配 = 最小点覆盖 = 总点数 - 最大独立集。
于是跑完 Dinic 后求最大独立集的补集, 在残留网络上跑 dfs ,
选择左边点集没取到的和右边点集取到的(这一步是选出补集),
再存一下边就做完了。口胡一下正确性, 左边点集取到了说明没有被匹配过,
一定在最大独立集里, 而为了 "独立" , 右边就要取取到过的点了,
因为我们还要取补集, 便得到了上述的结论。
代码:link
Codeforces round 818 (#Div2) 22/9/2
\((1650\rightarrow1701,
rk773)\)
八发罚时可谓是人麻了, 甚至交上去一发带 freopen 的, C 糊过的, D
抄的自己的逆元板子, 我对这场的评价是有思维性, 因为 A 就卡了十分钟……
E
题意:
给你 \(N\) , 让你计算 \(\sum lcm(c,gcd(a,b))\) , 对于所有满足 \(a+b+c=N\) 的三元组,
所有数都是正整数。
思路:
小清新数论题, 找一个刁钻的角度枚举, 一眼瞪出枚举 \(gcd(a,b)\) , 然后不会力。
设 \(gcd(a,b)=t\) , 原式转化为 \(\sum lcm(c,t) \sum_{a+b=N-c} [gcd(a,b)=t]\)
看上去是无用的转换, 问题是如何计算 \([gcd(a,b)=t]\) 的个数, 但聪明的你两眼瞪出
\(gcd(a,b)=t \Leftrightarrow gcd(\frac{a}{t},
\frac{b}{t})=1\) , 又想到了此时 \(\frac{a}{t}+\frac{b}{t}=\frac{N-c}{t}\) ,
三眼又瞪出一个重要结论:
若正整数 a+b = c , 则 a 与 b 互质的充要条件是 a 与 c
互质
证明很简单, 若 \(gcd(a,b)=u>1\) , 则
\(u|c\) , \(gcd(a,c)>0\) ;
若 \(gcd(a,c)=u>0\) , 则因为 \(b=c-a\) , \(u|b\) , 矛盾。
所以我们最后的结论是:
满足 \(gcd(a,b)=t\) 的式子个数, 即为与
\(\frac{N-c}{t}\) 互质的正整数个数, 即
\(\varphi(\frac{N-c}{t})\)
我们要求的转化为 \(\sum lcm(c,t)
\varphi(\frac{N-c}{t})\) , 注意 \(\frac{N-c}{t} \neq 1\) , 否则找不到正整数
\(a, b\)。
代码:link
F
题意:
给定长度为 \(N\) , 初始数组全为 \(0\) 的数组 \(b\) , 以及 \(m\) 对 \([u,v]\), 对于每对 \([u,v]\) , 你可以且必须选择 \(b[u]--, b[v]++\) 或 \(b[v]--, b[u]++\) 一次, 又给定一个 \(01\) 数组 \(s\) , 一个数组 \(a\) , 问是否存在一种选择方案, 使得: \[\forall s[i] \neq 0, b[i]=a[i]\]
思路:
点对就是点对, 即使它叫做 \([u,v]\)
也是点对, 你要把它看成一条边来搞网络流的话,
怎么保证这条边一定被选中呢?(我一开始还想再套个费用流, 寄!)
考虑原问题的等价条件, 一个 +1, 一个 -1, 等价于两个 \(b_{i}, b_{j}\) 都 -1, 再选一个 +2,
等价于两个 \(a_{i}, a_{j}\) 都 +1,
再选一个 -2, 问题转化为图的匹配, 无向边就没了, 把点对看成点, 往 u, v
各连一条容量为 1 的边, S(源点) 连点对, a 数组(对应的 \(s[i] \neq 0\) 的部分)连 T(汇点), 容量为
\(a_{i}/2\) ;
如何保证所有的点对都被用掉? 我们可以让那些点对在 \(s[i]=0\) 的 \(a[i]\) 上 "宣泄" 流量, 让 \(s[i]=0\) 的点连一条 inf 流量的边到中转点,
再从中转点连一条容量为 \(M-\sum
a_{i}[s[i]==1]\) 的边到汇点。
然后贺你的 Dinic 模版, 再检查一下流量大小与方向, 就行了。
代码:link
有很多小细节, 总的流量要为 M, \(s[i]=1\) 的 \(a[i]\) 流量要跑满, \(a[i]\) 更新后不为正偶数直接退出。
Codeforces round 819 (#Div1+2) 22/9/6
UNRATED
早上到机房一看, 出题人抄了 F 题(本场 A-H, 135mins)被发现, unrated
了, 乐。
反正我也做不到 F......, 补题还是要补的, 昨晚打的很奇妙, 个人体验 B
>> C , 反正 B 我还猜了一个小结论, 用时 30 mins(寄定了), C 只用了 6
mins, 剩下 90 mins 在 DEF 之间来回跳, 0:30 熬不下去了, 3
题含恨离场。
D
题意:
\(N\) 个点, \(M\) 条边, 联通的无向图, 无自环, 重边, \(M \leq N+2\) , 给你图的结构,
对边进行红蓝染色, 设只考虑红色边时的联通分量数为 \(c_{1}\) , 只考虑蓝色边时的联通分量数为
\(c_{2}\) , 问一种染色方法使得 \(c_{1}+c_{2}\) 最小。
思路:
生成树肯定是要求的, dfs 一遍即可, 剩下最多 3 个点(N+2-(N-1)=3)
全部染成另外一种颜色(这里指蓝色吧), 若最小化 \(c_{1}+c_{2}\) , 则剩下的 3 个点不能成环,
我们要选择一条环上的边, 染成红色, 环转移到了生成树上,
我们再把这条边的一个端点连接的其他所有边染成蓝色,
这样我们保留了生成树的同时也拆掉了环。
代码:link
E
题意:
对于一个长度为 \(n\) 的排列 \(p\) , 若当 \(1
\leq i \leq n\) 时都有 \(|p_{i}-p_{i}^{-1}| \leq 1\) 时我们称它是
"几乎完美" 的。(\(p_{k1}^{-1}=k2\)
当且仅当 \(p_{k2}=k1\))
给你排列的长度 \(n\) (\(n \leq 3e5\)), 求出所有 "几乎完美" 的排列,
对 998244353 取模。
思路: 咕, 等我学学排列组合, 不会推这个东西。
Educational codeforces round 136 (#Div2) 22/9/8
\((1701\rightarrow1675,
rk1841)\)
只会 ABC, 事实证明, 在 edu round , 所有你不会的 STL 都会攻击你……, 写 C
还被迫学了 multiset , 一看 \(\color{black}{j}\color{red}{iangly}\)
的代码才发现, 原来只要 priority_queue 啊……, 不过这和我是 ABC
战神没有半点关系, 因为我 D 的 DP 又寄了。
D
题意:
两人对弈(Alice & Bob),
轮流在给定字符串的头或尾处取走一个字符(Alice 先取),
加到自己字符串的开头, 保证字符串长度 \(N\) 为偶数, 问在最优情况下,
谁的字符串字典序最小(或是平局)。
思路:
要么 Alice 胜利, 要么平局。 因为最后剩两个字母时 Alice
总可以选取字典序最小的在最前面, 若两字母相同, 则 Alice
之前还是可能有选取更小字典序的机会, 对 Alice 而言最坏是平局。
让我们用 \(f_{i,j}\)
表示当字符串为给定字符串 \([i,j]\)
的子串时游戏的赢家, \(f_{i,j}=1\) 为
Alice 获胜, \(f_{i,j}=0\) 时为平局,
\(f_{1,N}\) 即为答案。
我们从小区间向大区间递推, 先初始化所有的 \(f_{i,i+1}\) 。
\[s[i]=s[i+1]
\;?\;f_{i,i+1}=0\;:\;f_{i,i+1}=1\] 然后我们向上递推到长度为
\(4, 6, 8, ......\)
的区间。每个上级区间可以看出实际上是由三个重复的下级区间构成的,
我们可以设为 \(a,b,c\) ,
目前我们要递推的区间为 \(f_{i,j}\)
1. \(f_{a}+f_{b}+f_{c}=3, \;
f_{i,j}=1\) 显然。 2. \(f_{a}+f_{b}+f_{c}=2\)
2.1. \(f_{a}=0 \; || \; f_{c}=0, \;
f_{i,j}=1\) 最左边 / 最右边是平局态, Alice 可以破坏。
2.2. \(f_{b}=0 \; \&\& \; s[i] \neq
s[j] , \; f_{i,j}=1\) 中间是平衡态, Alice
可以抢两边字典序小的字符的先手。
2.3. \(f_{b}=0 \; \&\& \; s[i] = s[j]
, \; f_{i,j}=0\) Bob 跟 Alice 对偶着下就平局了。
3. \(f_{a}+f_{b}+f_{c}=1\)
3.1. \(f_{a}=0 \; \&\& \; f_{c}=0, \;
f_{i,j}=0\) Bob 可以破坏掉中间 Alice
的胜利状态并留下一个平局状态。
3.2. \(f_{b}=0 \; \&\& \; s[i]=s[j],
\; f_{i,j}=0\) 中间平局, 两边无法抢先手, 最终平局。
3.3. \(f_{b}=0 \; \&\& \; s[i] \neq
s[j], \; f_{i,j}=1\) 中间平局, 两边可以抢先手, 最终 Alice 胜。 4.
\(f_{a}+f_{b}+f_{c}=0\)
4.1. \(s[i]=s[j], \; f_{i,j}=0\)
中间平局, 两边无法抢先手, 最终平局。
4.2. \(s[i] \neq s[j], \; f_{i,j}=1\)
中间平局, 两边可以抢先手, 最终 Alice 胜。
看着很难, 事实上写的时候很自然, 评分顶多2000,
至于如何不重不漏的转移, 你补题的时候 WA 6发就知道了,
话说应该我转移重了很多......, 不管了。
代码: link
E
题意:
有 \(N\) 盘菜,
每盘加入一个红胡椒或黑胡椒获得 \(a_{i}\) 或 \(b_{i}\) 的美味值,
不能都加/都不加/加入超过一个胡椒。
有 \(M\) 家店,
每家卖出一份红胡椒或黑胡椒包含 \(x_{j}\) 或 \(y_{j}\) 的对应胡椒,
你需要输出分别仅在第 \(j\)
家店买得所有胡椒并恰好用完所获得的最大美味值,
若不存在方案输出 \(-1\)。
思路:
小清新数论题, \(exgcd\), 三分,
还考察了二元一次不定方程的通解, 好题。
对 \(a_{i}-b_{i}\) 排序, 获得用 \(i\) 个红胡椒与 \(N-i\) 个黑胡椒的最大美味值, 记为 \(v_{i}\)。
接下来对每对 \(x_{j}, y_{j}\) 做
\(exgcd\) , 先判断是否有解,
在记录有解情况下红胡椒/黑胡椒最少需要的份数 ,
再判断一次是否有解, 然后去做三分, 因为答案 \(v_{ans}\) 一定单峰。
代码:link ,
注释都在里面了, 不贴了
F
题意:
(来自官方题解) 给定 \(a\) 数组, 长度为
\(n\) , 确定每个 \(b_{i}\) 的值, 使得 \(a_{i}|b_{i}\) , 所有 \(b_{i}\) 不同, 且 \(\sum b_{i}\) 最小。\(n \leq 1000, 1 \leq a_{i} \leq 10^6\)
。
思路:
(来自官方题解) 根据鸽笼原理, 对于每个 \(a_{i}\) , 只要考虑 \(1*a_{i}, 2*a_{i}, 3*a_{i}, ..., n*a_{i}\)
这几个 \(b_{i}\) 值,
问题可以转化为二分图最优匹配, 跑费用流的复杂度为 \(O(n^4)\) , 寄定了,
注意到全职在点上而不在边上, 我们就可以跑传统二分图。
具体来说, 我们的左侧点是从小到大排列的 \(b_{i}\) 集合, 右侧点是对应的 \(a_{i}\) , 这样我们便可以保证答案的最小性,
然而复杂度还是 \(O(n^4)\)
(左侧点决定主要复杂度, 太大了)。 一个优化是:不重置 \(vis\) 数组, 如果没有找到增广路,
它可以把复杂度优化到 \(O(M(E+V))\) , M
为最大匹配的大小, 这样复杂度便为 \(O(n^3)\) 。
代码:(来自本人) link
G
状压 DP + 数学, 爷不会!
Codeforces round 821 (#Div2) 22/9/19
\((1675\rightarrow1735,
rk592)\)
糊出来 D1, 但糊不出 D2, 算了, 能上小分就不错了……
D2
题意:
给定三个数 \(n, x, y\) , 其中 \(5 \leq n \leq 5000\) , 再给定两个长度为
\(n\) 的 01数组 \(a, b\) 。 你每次可以选择 \(a\) 中的两个位置, 让它们都异或 \(1\) , 若选择的位置相邻, 代价为 \(x\) , 否则代价为 \(y\) , 输出 \(a\) 数组变为 \(b\) 数组的最小代价, 若不存在则输出 \(-1\) 。
思路:
DP 是显然的, 注意到仅当 \(a, b\)
不同的位数是偶数时有解, 两个位置 \(i,
j\) 操作的代价为 \(min(y,(j-i)*x)\) , 当 \(j-i=1\) 时代价为 \(min(2*y,x)\) ,
因为我们可以找一个远一点的中转点进行两次操作来改变 \(i,j\) 位置的值 。
当 \(x \geq y\) 时, 优先使用 \(y\) 代价的操作, 若不可避免的要使用 \(x\) 代价操作, 则取 \(min(2*y,x)\)。
当 \(x < y\) 时, 两个位置 \(i, j\) 操作的代价为 \(min(y,(j-i)*x)\) ,
此时没有上文的特例了。若在不相邻的一对位置上使用 \(x\) 操作一定更劣,
因为拆开来就能覆盖更多位置。所以我们从前往后枚举最后一个位置是否用 \(x\) 操作与前一个位置消除。
设 \(f_{i}\) 为前 \(i\) 个位置最小代价的两倍,
对于 \(i > 2\) :
\[f_{i}=min(f_{i-1}+y,f_{i-2}+2*x*(pos_{i}-pos_{i-1}))\]
其中 \(f_{1}=y,
f_{2}=min(2*y,2*x*(pos_{2}-pos_{1}))\) ,
可以看出我们巧妙分拆了贡献, 对于奇数项, 不管与不与前一项消除,
身上总是带着一个 \(y\) 的,
帮助了偶数项的转移。
代码:link
E
题意:
有一个 \(120*120\) 大小的棋盘,
左上角位置为 \((0,0)\) ,
每格上有一个传送带, 初始方向全部朝右, 从 \(0\) 时刻开始会发生:
1、每一秒在 \(0,0\) 放下一个球。
2、如果 \((i,j)\) 存在一个球,
则它会移动到 \((i,j)\)
传送带的下一个位置; 如果某个位置存在多个球, 则合并为一个;
如果下一个位置超出棋盘, 则丢弃。
3、每传送一次球, 传送带的方向就会变化; 原来向右变向下,
原来向下变向右。
1e4 次询问, 问第 \(t(t \leq
10^{18})\) 秒时, \((i,j)\)
是否有球, codeforces 原题链接里还有个图片流程示例, 就不贴了。
思路:
找规律/递推, 一个重要的性质是, 假设经过某个位置有 \(n\) 个球, 则被传到右边的球数为 \(\lceil \frac{n}{2} \rceil\) ,
被传送到左边的球数为 \(\lfloor \frac{n}{2}
\rfloor\) , 考虑通过差分前缀和算出第 \(t\) 秒是否有球经过, 设 \(f_{t,x,y}\) 为到第 \(t\) 秒为止时经过 \((x,y)\) 点的球的总数, 若 \(f_{t,x,y} \neq f_{t-1,x,y}\) 说明第 \(t\) 秒有球经过。
在具体操作中, 去除 \(t\) 维, \(f_{0,0}=max(0,t-x-y+1)\), \((f_{i,j}+1)/2 \rightarrow f_{i,j+1},\;f_{i,j}/2
\rightarrow f_{i+1,j}\) 推一下就行了。
代码:link
不是很理解这个 \(memset\) 复杂度 * 1e4
询问量 怎么过的掉……
Codeforces Round 822 (#Div2) 22/9/23
\((1735\rightarrow1792,
rk475)\)
构造, 一生之敌……构造 + E题 = 含恨离场。
但还是上分了, 好耶。
E
题意:
初始给定一个 \(b\) 数组, 构造一个
\(n * n\) 矩阵 \(a\) , 保证 \(n\) 为质数, 满足以下条件:
1、\(a_{i,i}=b_{i}, \;\forall \;0 \leq b_{i}
<n\)
2、\(a_{r1,c1}+a_{r2,c2}\not\equiv
a_{r1,c2}+a_{r2,c1} \; (mod\;n), \;\forall \;1\leq r_{1}<r_{2}\leq n,
1 \leq c_{1} < c_{2} \leq n, 0 \leq a_{i,j} < n\)
思路:
转化式子, 第二个约束条件等价于:
\[a_{r1,c1}-a_{r1,c2}\not\equiv
a_{r2,c1}-a_{r2,c2} \;(mod\;n)\]
于是我们只要让每一行为公差不同的等差数列即可, 公差为 \([0,n-1]\)。
现在考虑第一个性质, 要满足角标元素, 可以这么构造:
\[a_{i,j}=(i*(j-i+n)+b_{i})\]
这样子 \(i\) 承担了公差的使命, \(i=j\) 时 \(a_{i,j} \; mod \; n =b_{i}\) , 后面加个
\(n\) 防止取模取出负数。
代码:link
官方题解更厉害, 直接给出了构造的通用二次多项式……,
这题构造方法极多, 场上一个没想出来有点离谱。
F
题意:
给你一个无限长度的 \(\tt{Thue-Morse\;sequence}\),
通过如下方式构造, 初始字符串 \(s = 0\)
, 接下来无限步中, \(s=s\;+\; inv(s)\) ,
其中 \(inv(s)\) 为 \(s\) 按位取反得到的字符串, \(\bf Example: 0
\;01\;0110\;01101001\;0110100110010110\;...\)。
给定两个数 \(n, m \leq 1e18\) , 问
\(s\) 长度为 \(m\) 的两个子串 \(s[0,m-1], s[n,n+m-1]\) 有多少处不同?
思路:
二进制考虑手玩一些性质, 我将每个数对应它们的二进制下标可以发现:下标中
\(1\) 的数目为奇数, 对应数位为 \(1\) , 下标中 \(1\) 的数目为偶数, 对应数位为 \(0\) 。换言之, \(s[i]=\_\_builtin\_parity(i)\) , 效率是
\(O(n)\) 的, 显然不够, 我们要找一种只带
\(log\) 的做法 ,
想到这里我就寄了去看题解。
考虑递归推式子, 我们简记 \(\_\_builtin\_parity(i)=par(i)\) , 问题是求
\(f(n,m)=\sum\limits_{i=0}^{m-1}{[par(i) \neq
par(n+i)]}\) , 当 \(m=0\) 时,
\(f(n,m)=0\) , 当 \(m=1\) 时, \(f(n,m)=[par(0) \neq
par(n)]=par(n)\)。
为了方便讨论, 我们可以固定 \(m\)
的奇偶性, 让我们固定 \(m\) 为偶数,
因为这样可以方便递归, 在 \(m\)
为奇数时拆出最后一项, \(f(n,m)=f(n,m-1)+[par(m-1) \neq
par(n+m-1)]\) 就可以了; 接下来我们分类讨论 \(n\) 的奇偶性, 若 \(n\) 为偶数, 观察 \(par()\) 的特性, 因为 \(par(2k) \neq par(2k+1)\) , 同理 \(par(2k+n) \neq par(2k+n+1)\) ,
所以有恒等式:
\[[par(2k) \neq par(n+2k)]=[par(2k+1) \neq
par(n+2k+1)]\]
成立, 设 \(2k=i\) , 发现又变为了 \([par(i) \neq par(n+i)]\) 的形式,
所以有:
\[
\begin{aligned}
f(n,m) &= \sum\limits_{i=0}^{m-1}{[par(i) \neq par(n+i)]}\\
&=2 \sum\limits_{k=0}^{m/2-1}{[par(2k) \neq par(n+2k)]}\\
&=2 \sum\limits_{i=0}^{m/2-1}{[par(i) \neq par(n/2+i)]}\\
&=2* f(n/2,m/2)
\end{aligned}
\] 若 \(n\) 为奇数,
同理有恒等式: \[[par(2k) \neq
par(n+2k)]=[par(2k) = par(n+2k-1)]\]
注意这里是 \(-1\) 而不是 \(+1\) ,
奇数保证能与它前面的偶数二进制位相反,
与后面的偶数的二进制位关系则是不确定的, 同理还有: \[[par(2k+1) \neq
par(n+2k+1)]=[par(2k)=par(n+2k+1)]\]
所以我们可以把 \(2k, 2k+1\) 都转为
\(2k\) 然后向下递归。
\[
\begin{aligned}
f(n,m) &= \sum\limits_{i=0}^{m-1}{[par(i) \neq par(n+i)]}\\
&= \sum\limits_{k=0}^{m/2-1}{\Big([par(2k) \neq
par(n+2k)]\;+\;[par(2k+1) \neq par(n+2k+1)]}\Big)\\
&= \sum\limits_{k=0}^{m/2-1}{\Big([par(2k) =
par(n+2k-1)]\;+\;[par(2k) = par(n+2k+1)]}\Big)\\
&= \sum\limits_{i=0}^{m/2-1}{\Big([par(i) =
par((n-1)/2+i)]\;+\;[par(i) = par((n+1)/2+i)]}\Big)\\
&=m\;-\;f((n-1)/2,m/2)\;-\;f((n+1)/2,m/2)
\end{aligned}
\] 最后一行因为不等号变等号进行了容斥。
状态数为 \(O(log\;n\;log\;m)\) ,
进行记忆化搜索即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
typedef pair<int,int> PII;
int T, N, M;
map<PII,int> mp;
int par(int x) {return __builtin_parityll(x);}
int f(int n, int m){
if(m==0) return 0;
if(m==1) return par(n);
if(m%2==1) return f(n,m-1)+(par(m-1)!=par(n+m-1));
if(mp.count(make_pair(n,m))) return mp[make_pair(n,m)];
int ans=0;
if(n%2==0) ans=2*f(n/2,m/2);
else ans=m-f((n-1)/2,m/2)-f((n+1)/2,m/2);
return mp[make_pair(n,m)]=ans;
}
signed main(){
cin >> T;
while(T--){
cin >> N >> M;
mp.clear();
cout << f(N,M) << '\n';
}
return (0-0);
}
有好想但难写的正统数位 DP 做法, 可能以后更新。
Codeforces Round 823 (#Div2) 22/9/25
\((1792\rightarrow1672,
rk4583)\)
只会 AB, 一把掉干, 但是心态又比上次进步了许多......, B
题就糊了个三分上去就离谱, C 题简单字符串上贪心没调出来,
我想这也是算法竞赛的一部分, 不爽不要玩……
然而我还得玩, 在度过糟糕的一晚后过来补题了……
C
题意:
\(0\) 到 \(9\) 组成的字符串 \(s\) , 你可以随时取出一位数字 \(d\) , 再插入 \(min(d+1,9)\) 到任意位置,
问你能得到的字典序最小字符串。
思路:
从后往前更新, 因为要把字典序小的甩到前面,
大的放到后面去。动态更新最小值, 将大于最小值的全部甩到后面就行了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13string s;
cin >> s;
int cnt[10]={};
int x=9;
for(int i=s.size()-1;i>=0;i--){
if(s[i]-'0'<=x){
x=s[i]-'0';
cnt[s[i]-'0']++;
}
else cnt[min(s[i]-'0'+1,9)]++;
}
for(int i=0;i<=9;i++) cout << string(cnt[i],'0'+i); // cnt[i] 个 '0'+i 字符
cout << '\n';
D
题意:
两个只包含小写英文字母且长度为 \(n(n \leq
1e5)\) 的字符串 \(s_{1}, s_{2}\)
, 你每次可以交换长度为 \(k(1 \leq k \leq
n)\) 的 \(s_{1}\) 的前缀与 \(s_{2}\) 的后缀, 问是否能使得 \(s_{1}=s_{2}\) ?
思路:
观察每次我们所做的:交换 \(s_{1}[1...i]\) 与 \(s_{2}[n+1-i...n]\) , \(s_{1}[i]\) 与 \(s_{2}[n+1-i]\) 不可能处于同一个串中,
且始终对称。
接下来一个可以手玩出的结论是:对于一对 \(s_{1}[i],s_{2}[n+1-i]\)
可以在保证它们对称的前提下随意调整它们的位置。一种构造是, 设 \(op(k)\) 为一次操作, 交换长度为 \(k\) 的 \(s_{1}\) 的前缀与 \(s_{2}\) 的后缀, 一次 \(op(k)\) , 一次 \(op(k+1)\) 可以视为一组操作, 在 \(s_{1}, s_{2}\) 的前 \(k+1\) 位上轮换,
最终我们都能调整字符对到我们想要的位置, 只要从大到小轮换就可以了。
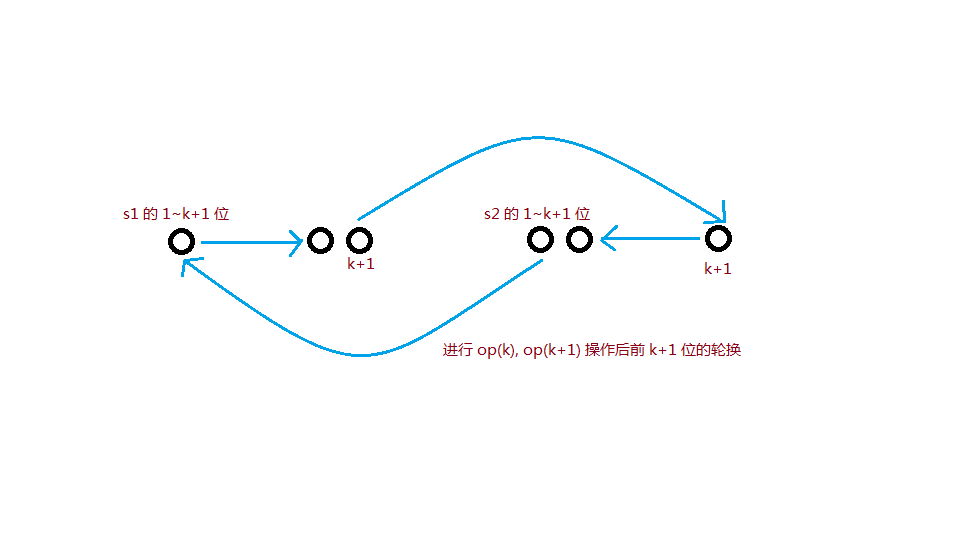
Windows画图好难受
所以, 能使得 \(s_{1}=s_{2}\) ,
当且仅当对于所有对称字符对\((a,b)(a \leq
b)\) :
1、\(a \neq b\) , \((a,b)\) 的出现次数是偶数(\(s_{1}[i]=s_{2}[n+1-i], \;
s_{1}[n+1-i]=s_{2}[i]\))
2、\(a = b\) , 仅在 \(n\) 为奇数时最多出现一对出现次数为奇数的
\((a,b)\) , 可以安插在中间(事实上……
\(n\) 不用判奇偶……想想为什么)。
代码:link
E
题意:
给你长度为 \(n(n \leq 5e5)\) 的数组
\(a(a_{i} \leq 1e6)\) ,
问你有多少段区间 \([l,r]\) 满足 \(min\{a_{l...r}\}|max\{a_{l...r}\}\)
。
思路:
值域这么小能不能用一用啊……好像不行……是用来分解质因数的……
区间的选择有 \(n^2\) 种,
区间最大值的选择只有 \(n\) 种,
这句话来自 codeforces exercises 1 的第一场比赛的第一篇题解,
现在又用上了。
让我们同理处理 \(a_{i}\) 左边/右边
第一位比它 大/小 的数字的下标, 记为 \(rmax_{i}, rmin_{i}, lmax_{i}, lmin_{i}\),
其中 \(lmax_{i}\)
特殊定义为左边第一位大于等于 \(a_{i}\) 的数的下标, 当:
\[lmax_{i} < l \leq i \;\;\&\&\;\;
i \leq r < rmax_{i} \;\;(1)\]
时, \(a_{i}=max\{a_{l...r}\}\) , 在
\((1)\) 的前提下, 我们枚举 \(a_{i}\) 的除数 \(j\) 作为最小值, 设左边离 \(i\) 最近的最小值为 \(j_{1}\) , 要满足:
\[lmax_{i} < l \leq pos_{j_{1}}
\;\;\&\&\;\; pos_{j_{1}} < i \;\;\&\&\;\; i <
rmin_{pos_{j_{1}}}\]
设右边离 \(i\) 最近的为 \(j_{2}\) , 也同理,
\[pos_{j_{2}} \leq r < rmax_{i}
\;\;\&\&\;\; pos_{j_{2}} \geq i \;\;\&\&\;\; i >
lmin_{pos_{j_{2}}}\] 最难理解的部分是去除重复统计的区间,
官方题解简直是谜语人附体, 思路是这样的, 枚举 \(j_{1}\) 的区间可以包含 \(j_{2}\) , 枚举 \(j_{2}\) 的区间时不能包含 \(j_{1}\) , 如果只有 \(j_{1}\) 或只有 \(j_{2}\) 照常枚举, 如果 \(ar_{i}=j_{1}\) 那么实际上是 \(ar_{i}=j_{2}, j_{1}=ar_{i}\) 因为无法满足
\(lmax_{i} < l \leq pos_{j_{1}}\) ,
这也是定义 \(lmax_{i}\)
时要取等号的原因, 你也可以不在 \(lmax\)
上取等号而在 \(rmax\) 上取等号,
效果是一样的......
然后统计区间的个数, 加一加就行了, 复杂度 O(能过), 因为有 5s。
代码:link,
里面也有一些注释……具体实现要枚举因子, 储存 \(pos\) 与下一个下标 \(idx\) , 单调栈处理 \(lmax,lmin,rmax,rmin\) 等等......
F
咕~
Educational Codeforces Round 136 (#Div2) 22/9/29
\((1672\rightarrow1578,
rk4496)\)
继续下分, 好耶, specialist again!
早上起来发现自己 B 被 hack 了……讨厌 edu round,
只算题数不算分数导致我掉到了 4000 多名……D 是个二分还做不出来,
因此我们应该 "Stop learning useless algorithms......"
D
题意:
给定一颗以 \(1\) 为根节点的树,
每次操作可以移植一颗子树到根的下部, 问 \(k\) 次操作后最大深度的最小值。
思路:
二分这个最大深度, 从树的底部向上更新,
若一段长度大于等于这个最大深度就接到根节点上去,
注意根节点与根节点的子节点不更新。
代码:link
E
题意:
给你一个 \(2* n\) 的矩阵, 一些格子是
"脏" 的, 另一些是干净的, 分别用 \(1,0\)
表示。机器人从 \((1,1)\)
开始清理脏格子, 每次朝离它最近的脏格子移动,
若在任意时刻离它最近的脏格子有多个就会停机,
问存在机器人不停机且清理完脏格子所需要预先移除的最少的脏格子数量, \(n \leq 2e5\) 。
思路:
显然这题没有这么显然。
后面的格子会隐隐对前面的格子形成控制之势, 如图:
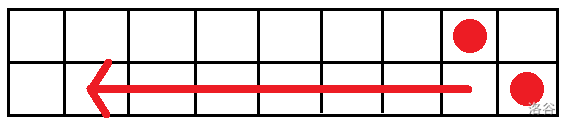
考虑倒推, 设 \(f_{i,j}\) 表示机器人从
\((i,j)\)
出发需要预先移除的最少的垃圾数量, 进行分类讨论, 设当前在处理 \(f_{i,j}\)。
下文的转移建立在它本身条件以及上文条件的基础上:
1、\(f_{i \oplus 1, j}=0\) ,
此时最近的就是下一列的脏格子, 本列已经处理完毕, 转移为 \(f_{i,j}=f_{i+1,j}\) 。
2、\(f_{i+1,j}=0\) ,
此时下一列对应行没有脏格子, 我们可以直接过去并移除本列的脏格子,
也可以从另一行绕过去, 转移为 \(f_{i,j}=min(f_{i+1,j}+1,f_{i+1,j \oplus
1})\)
3、\(f_{i+1,j \oplus 1}=0\) ,
此时状态是这样的:
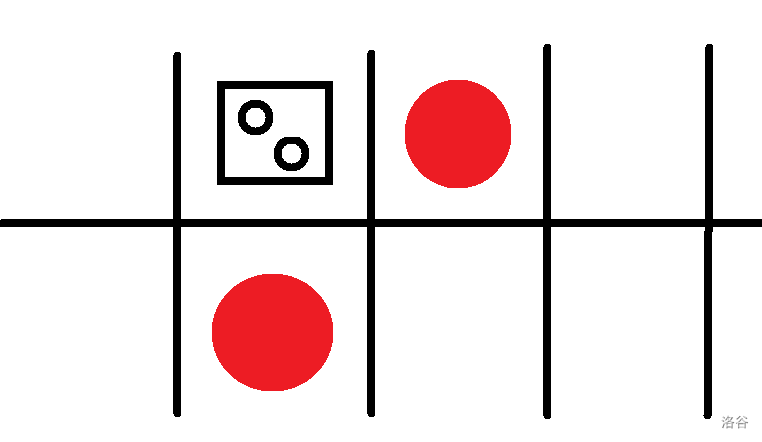
可以看到小机器人已经被包围了!我们必须去掉一个脏格子,
同时我们转移到两列后而不是一列后, 因为我们已经规定了下一列的状态,
转移为:\(f_{i,j}=min(f_{i+2,j}+1,f_{i+2,j
\oplus 1}+1)\) 。
4、\(f_{i+1,j \oplus 1}=1\) ,
此时状态是这样的:
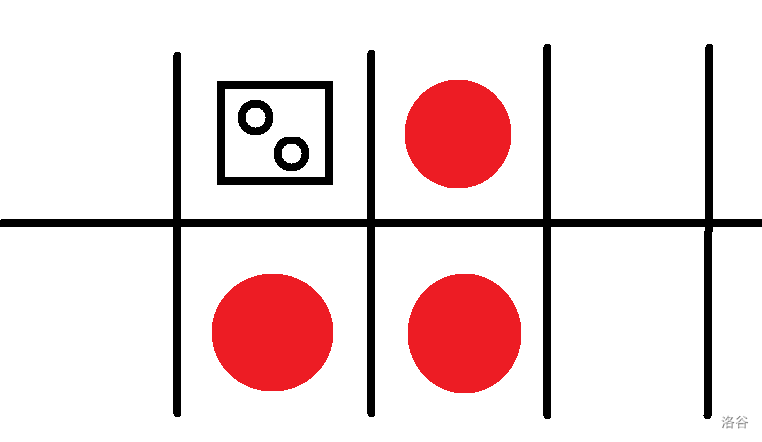
要么移除下面两个, 从上面走, 要么移除上面一个, 从下面走, 转移为:\(f_{i,j}=min(f_{i+2,j}+2,f_{i+2,j \oplus
1}+1)\) 。
代码:link
很短很好懂。
F
于 22.11.18 7:30~15:00 补题, 因为处理字符串的失误调的上头,
中间听完了四五遍 toe 的专, 很好的平复了情绪, 进行一个无关的推荐。
题意:
(字符集大小为 12, 即前 12 个英文字母)
有 \(n \leq 1000\) 个单词,
每个单词的相邻字符不相同, 每个单词有一个权值 \(c \leq 1e5\), 每个单词长为 \(s \geq 2\) , 保证 \(\sum s \leq 2000\)。
你要设计一个长度为十二的数组作为键盘, 使每一位对应字符集的一个字符,
不重不漏。若一个单词所有相邻的两个字母在键盘上也相邻,
你可以得到单词所对应的权值(称为单词能在键盘上被简单输出),
请输出一种获得最大权值和的数组构造方案。
思路:
我们可以把每个单词想象成最多只有十二个节点的无向图,
单词中每两个相邻的字符代表无向图中的一条边。 显然有一些 “图”
的权值我们不可能得到, 例如在图上有环的时候或者这个图有一些点的度 \(\geq\) 3 的时候。
如果一个单词能在键盘上被简单输出, 例如 "abcb" , 它对应的无向图为 a-b-c ,
实际上是一条链, 这个链在键盘上可能会有两种排列:abc 与 cba。
我们把所有合法的链的两种排列对应的字符串拉去建立AC自动机,
在每个单词末尾加入权值 \((t[u].v+=val)\) ,
每个节点顺便也加上它对应的 fail 子树上所有节点的权值, 这个在连 fail
边时可以顺便进行, 因为如果一个单词在某个节点完成匹配, 它的 fail
边连接的是这个节点所代表单词的最长后缀, 一定也完成了匹配。
我们的目标是找到一个 \(a-l\) 的排列,
我们可以用状压DP的思想来做这个, 设计 \(f[s][i]\) 表示当前选取的字符集和状态为
\(s\) , 当前处于 trie 图上的 \(i\) 号节点时能得到的最大权值和, 转移 \(f[s][i]\) 需要在最外层枚举状态 \(s\) , 内层枚举当前节点 \(i\) , 最内层再枚举当前节点的子节点,
复杂度为 \(2^{12} * 2^{12} * 12\)
但因为跑不满 + 4s 时限所以还是可行的。
对于每个状态为 \(s\) 的可行节点 \(u\), 当我们枚举到它的 \(j\) 号儿子时的转移方程为:
\[ f[s \oplus 2^j][t[u].s[j]]=max(f[s \oplus
2^j][t[u].s[j]], f[s][u]+t[s \oplus 2^j].v)\]
我们处理出来最大值, 然后随便选一个等于最大值的 \(f[2^{12}-1][i]\) ,
再逆着它回溯就能找到一种可能的键盘布局了。
代码:link
细节很多, 你不妨想想怎么把一条链对应的两个字符串拉出来, 然而我写的这一切
\(\color{black}{j}\color{red}{iangly}\)
十九分钟就写完了, 而我得用 190 行加上五六个小时。
Codeforces Global Round 22 22/9/30
\((1578\rightarrow1531,
rk3457)\)
……
来看题……
C
题意:
一个数组, Alice 和 Bob 轮流拿数, Alice 先手, 最后 Alice
拿到的数之和为偶数则 Alice 赢, 问在双方最优情况下谁赢。
思路:
分类讨论, 设奇数个数为 \(x\) ,
偶数个数为 \(y\) , 则:
1、\(x \; mod \; 4=0\) , Alice 必胜,
可以保证 Alice 拿到一半的奇数。
2、\(x \; mod \; 4=1, y \; mod \; 2=0\)
, Alice 必败, Bob 跟着 Alice 拿, 可以保证 Alice 拿到奇数个奇数。
3、\(x \; mod \; 4=1, y \; mod \; 2=1\)
, Alice 可以保证让 Bob 拿到第一个奇数, 从而拿到偶数个奇数。
4、\(x \; mod \; 4=2\) , Alice 必败,
Bob 可以保证 Alice 拿到奇数个奇数。
5、\(x \; mod \; 4=3\) , Alice 必胜,
Alice 先拿一个奇数, 此时转化为上一种情况, Alice 可以保证 Bob
拿到奇数个奇数, 从而自己拿到偶数个奇数。
代码:link
D
题意:
对于一个排列 \(a_{1},a_{2},...,a_{n}\) , 以及一个整数
\(k(0 \leq k \leq n)\) ,
以如下的方式计算 \(b\) 数组:
$; i , x=a_{i}, $
1、\(x \leq k\) , 设置 \(b_{x}\) 为满足 \(1 \leq j < i \;\;\&\&\;\; a_{j} >
k\) 的最后一个 \(a_{j}
(b_{a_{i}}=a_{j})\) , 若不存在这样的 \(j\), \(b_{x}=n+1\)
2、\(x > k\) , 设置 \(b_{x}\) 为满足 \(1 \leq j < i \;\;\&\&\;\; a_{j} \leq
k\) 的最后一个 \(a_{j}
(b_{a_{i}}=a_{j})\) , 若不存在这样的 \(j\) , \(b_{x}=0\)
给定 \(b\) 数组, 让你求一个满足条件的
\(a\) 数组与 \(k\) , 题目保证存在。
思路:
做 permutation 题, 关键是看出它的操作到底想干什么,
不要被下标套娃绕晕了, 例如这题如何求 \(k\) ? 观察到它把下标 \(\leq k\) 的数变为 \(> k\) 的数, 我们只要统计 \(b_{i}>i\) 的数目便可求出 \(k\) ,
不用跟我开始一样顺着排列黑白染色……。
接下来开始不断手玩样例, 可以发现一个结论: \(b_{a_{l}}=b_{a_{r}}\) , \(\forall t \in [l,r], b_{a_{t}}=b_{a_{l}}\)
。用人话来讲, \(b\)
数组中值相同的位置处于 \(a\)
数组中连续的一段。
对于样例 7 7 7 3 3 3 的答案是: k=3, a=1 2 3 4 5 6, 在这里 \(a\) 中的 1&2 可以互换, 4&5&6
也可以互换, 在连续的一段中仅存在最后的 3 不能移动, 因为它推导了 \(b\) 数组剩下的部分。
我们每次显然可以先确定 \(b\) 数组中
\(0\) 和 \(n+1\) 所对应的位置, 我们可以将 \(b\) 数组放到一个 \([0,n+1]\) 的桶中,
寻找唯一的"推导数"再往后推导, 最后构造出整个 \(a\) 数组。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21N=read(); a.clear();
for(int i=0;i<=N+1;i++) v[i].clear();
int n1=0, now=0;
for(int i=1;i<=N;i++){
br[i]=read();
if(br[i]>i) n1++;
v[br[i]].push_back(i);
}
if(v[N+1].size()) now=N+1;
int cnt=1;
while(cnt<=N){
cnt+=v[now].size();
for(auto &u:v[now]){
if(v[u].size())
swap(u,v[now].back()); //把“推导数”放到最后
}
a.insert(a.end(),v[now].begin(),v[now].end());
now=v[now].back();
}
cout << n1 << '\n';
for(auto u:a) cout << u << " "; cout << '\n';
E
题意:
给定一个非负整数数组 \(a\) , 长度为
\(n(n \leq 1e5)\) ,
计算有多少种分割使得分割后的每一段的和构成的数组是一个回文数组。
思路:
\(0\) 在里面搅屎。
没有 \(0\) 很好做, 双指针弄一下,
找出所有对称的分割点组, 每组有选或不选之分, 弄一下就行了。具体而言, 设
\(f_{i,j}\) 为子序列 \([i,j]\) 中切分的方案数, 假设 \(x\) 是最小的满足存在一个 \([i,j]\) 的后缀等于 \(x\) 的前缀的位置(值可以为
0), 设这个后缀的位置为 \(y\) ,
则有 \(f_{i,j}=2 * f_{x,y}\)。
现在考虑中间有 \(0\) 的情况,
上文的假设不变, \(x\)
后面第一个非 0 位置为 \(l\) , \(y\) 前面 第一个非零位置为
\(r\) , 我们便可以调整分割的位置,
或者多分割几刀构成几个对称的 \(0\)
区间。
设 \(len=min(l-x,y-r)\) ,
我们可以在中间切 \([0,len]\) 刀,
此时的转移为\[f_{i,j}=
\sum\limits_{k=0}^{len}{l-x \choose k}{y-r \choose
k} f_{x,y}\]
然后我们递归求解这个问题。
代码:link
注意 \([x,y]\) 中间全为 \(0\) 部分的特判。
F
题意:
交互题, 给你一个 \(n(n \leq 1000)\)
的无向图, 告诉你每个点的度, 你要给每个点染色, 满足:
1、同一个颜色的所有点在同一个联通块内。
2、同一种颜色(\(c\))的所有点的度(\(s_{c}\))之和小于等于点数的平方(\(s_{c} \leq n_{c}^2\))。
你可以做至多 \(n\) 次询问,
每次询问一个点, 若当前询问是针对该点的第 \(k\) 次询问, 则回答该点连接的第 \(k\) 条边所连接的另一个顶点。
要求你最终给出一种染色方案, 保证存在这样的方案。
思路:
糊了个贪心上去, 只与正解差一个 \(\tt{break}\) , 不知是幸运还是不幸……
直觉上讲肯定是从度数大的点开始询问, 设当前询问点为 \(u\) , 我们以这样的算法来 bfs:
1、询问到的节点 \(v\) 未被访问过,
我们把 \(v\) 合并进 \(u\) 的联通块。
2、询问到的节点 \(v\) 被访问过, 我们把
\(u\) 合并进 \(v\) 的联通块,
并break
下面我们证明这种贪心的正确性, 我们实际上在构建一个森林, 当 \(u\) 的所有节点都未被访问过时, 设 \(u\) 点的度为 \(d_{u}\) , 有 \(s_{c} \leq d_{u}* (d_{u}+1) < (d_{u}+1)^2 =
n_{c}^2\) , 满足条件。
当 \(u\) 的某个连接点 \(v\) 访问过时, \(v\) 所在的块设为 \(c'\) , 一定满足条件(\(s_{c'} \leq n_{c'}^2\)), 设 \(v\) 为 \(u\) 上第 \(i\) 个1遍历到的点, 将 \(u\) 与前 \(i-1\) 个点加入这个块, 此时总节点数为 \(n_{c'}+i\) , 度数和小于等于 \(s_{c'}+i* d_{u}\) , 此时 \(d_{u} \leq n_{c'}\) ,
因为我们是从度数大的节点到度数小的节点遍历的, 所以有:
\[s_{new_c}=s_{c'}+i* d_{u} \leq
n_{c'}^2+i* d_{u} \leq n_{c'}^2+ i* n_{c'} < (n_{c'}+
i)^2= n_{new}\]
于是做完了, 怎么感觉这个上界松松的……? 自己看起来与题解只差了一个 \(\tt{break}\) , 事实上没有证明什么正确性,
差的有点远, 但这样都过了五个点总是会让人产生一点错觉……
代码:link
Codeforces Round 824 (#Div2) 22/10/2
\((1537\rightarrow1543,
rk1898)\)
……
来看题……
D
为什么考场上摆烂不写, 为什么……
到学校补题, 不看题解 17mins 写+调就过了, 比我一些 B
题用的时间都短……
题意:
\(n\) 张牌(\(n \leq 1000\)), 每张牌有 \(k\) 个维度 (\(k
\leq 20\)) , 每个维度有三种取值 0/1/2,
一组三张牌被称为"好的"当且仅当这三张牌的每一个维度的三个取值都相同或不同,
五张牌被称为一个"meta-set"当且仅当里面有两组及以上"好的"牌组, 给你 \(n\) 张牌, 保证互不相同, 问有多少个 meta-set
?
思路:
分别钦定每个数为 meta-set 中的重复数, 暴力枚举第二个数, \(map\) 查第三个数, 复杂度 \(O(20n^2+n^2\;log\;n), n \leq 1000\) ,
时限四秒只用 139ms, 然后没了。
代码:link
E
题意:
在数轴上有 \(n(n \leq 1000)\)
个非负整数点 \(h_{i}\) , 以及两个位置
\(p_{1}, p_{2}\) , 有对应的两个距离数组
\(d_{1}, d_{2}\) , 其中 \(d_{i,j}=|h_{j}-p_{i}|\) , \(d_{1}, d_{2}\) 内部的顺序被打乱了, 现在给你
\(d_{1}, d_{2}\) , 让你还原一个可能的
\(h\) 数组以及 \(p_{1}, p_{2}\) , 或报告不存在满足性质的
\(h,p_{1},p_{2}\) 。
思路:
1h 在机房憋了个假做法, 但可以对正解有部分启示。
我的想法是, 固定 \(p_{1}=0\) , 先把
\(d_{1},d_{2}\) 取反后的数组加入(\(n \to 2n\)), 再 sort \(d_{1},d_{2}\) , 把 \(d_{1}\) 扔进 \(map\) 里, 因为 \(\exists \; d_{2,i}\) 满足 \(d_{2,i}=d_{1,N}\) 或 \(d_{2,i}=d_{1,N+1}\) , 我们枚举这个 \(i\) , 保存偏移量, 然后看能不能找到大小为
\(n\) 的匹配。
这个贪心的问题是, 由于 \(d_{1},
d_{2}\) 各取反复制了一份, 失去了单调性。正解仅复制 \(d_{1}\) 的正负存进 \(map\) 中, 然后枚举 \(p_{2}=\pm d_{1,i} \pm d_{2,1}\) 中的 \(i\) 和 \(p_{2}\) 的四种情况来保证 \(d_{2,1}\) 的匹配, 然后贪心,
因为对称性我们只考虑 \(p_{2} \leq 0\)
的情况(一个负的和一个正的匹配, 对应一定有一个正的与负的匹配):对于 \(d_{2}\) 中的一个元素 \(x\) , 可能存在的匹配为 \(|p_{2}-x|\) 与 \(|p_{2}+x|\) , \(|p_{2}-x| \geq |p_{2}+x|\) , 所以我们可以将
\(d_{2}\)
从大到小排序并优先选择较大数匹配, 因为若当前不与较大数匹配,
则后续无法匹配。
代码: link
有点抽象, 调了一上午, 寄!
另一个思路:
考虑对于一个点, 要么到 \(p_{1},
p_{2}\) 的距离之和为 \(f\) ,
要么到 \(p_{1}, p_{2}\)
距离的绝对值之差为 \(f\) ,
我们的目标转为找到这个 \(f\) , 因为
\(\exists \; d_{2,i}\) 满足 \(d_{2,i}=d_{1,1}\) , 这两个点在同一个位置上,
我们可以枚举 \(f\) 的 \(2* n\) 种可能性(\(d_{1,1}+d_{2,i}\) 或 \(|d_{1,1}-d_{2,i}|\)) , 判断在钦定边长 \(=f\) 的情况下存不存在大小为 \(n\) 的匹配, dinic 之, 复杂度为 \(O(n^{2.5})\) 。
另一个代码: 待补,
dinic 之后不会维护捏
F
Dytechlab Cup 2022 22/10/7
\((1543\rightarrow1549,
rk2114)\)
B 题 WA on pretest 4 查了半天查不出来, 我是**
什么手速场, 赞助场是 div1+2 形式的, 一堆橙、红名还在 D 卡着呢……
D
题意:
无向图, \(n(n \leq 500)\) 个点, \(m(m \leq 250000)\) 条边, 有边权, 要从 \(1\) 点出发到 \(n\) 点,
你可以在出发前进行任意次如下操作:
选择 \(i\) 号边, 设其连接 \(u_{i}, v_{i}\) , 边权为 \(w_{i}\) , 选择 \(v_{i}\) 通过任意边连接的另一个顶点 \(t_{i}\) (\(t_{i}\) 可等于 \(u_{i}\)) , 断开 \(u_{i}, v_{i}\) 的连接, 连接 \(u_{i}, t_{i}\) , 此举将耗费 \(w_{i}\) 的时间, 边权不变。
问从 \(1\) 点出发到 \(n\) 点的最短时间。
思路:
\(n \leq 500, floyd\)。
为什么题干不简单的把边权翻倍? 因为一条边可能在图上"转来转去",
移到任何地方, 例如, 在 codeforces 上的这个样例中:
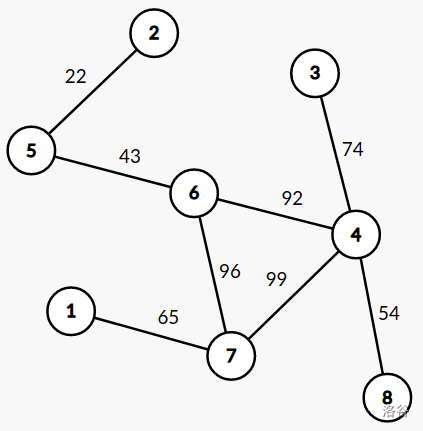
答案是 \(154\) , 2 <-> 5
之间边权为 22 的边移动了六次, 连接了起点和终点, 最后加上一次走边的代价,
22 * 7 = 154。
因为重边有用, 可以转出去, 存图时只要存图的连通性就好。
一个 \(key\; observation\) 是,
最短路一定可以直接连接 \(1\) 与 \(n\) 号点, 假设最短路不直接连接首尾, 例如 1
<-> u <-> v <-> N ,
我们可以直接选择最短路上的最短边让它两头扩展连接首尾,
现在我们只要处理每一条边是不是最短边就好。
1、若一条边本身就在起点到终点的路径里, 我们可以直接扩展它至首尾。
2、若一条边本身不在起点到终点的路径里, 我们让它探到路径上的一个点,
称为中转点, 再在这个点上收缩形成自环, 再伸展至首尾。
代码:
1 | int ans=inf; |
若有边 i <-> j, d[i][j]=d[j][i]=1, 然后跑 \(floyd\) 。
上面的 +1 是走边的代价, 下面的 +2 是走边的代价加上缩成自环的代价,
好题!
E
Codeforces Round 825 (#Div2) 22/10/10
\((1549\rightarrow1711,
rk224)\)
\(+162\) ! 只要你分数够低,
总有可能上大分!
D 的构造想出来了, C2 线段树不会, 在手速场(C1:5500通过
C2:102通过)小寄大赢!
B Wa 了两发, 下次想好再写题, 不然做不出 D 又掉到 1000 名左右去了……
C2
题意:
给你 \(a\) 数组, 长度为 \(n\) ,定义好数组 \([a_{l},a_{l+1},a_{l+2},...,a_{r}]\) 满足
\(\forall \; i, a_{i} \geq i-l+1, (a_{l} \geq
1, a_{l+1} \geq 2, ..., a_{r} \geq r-l+1)\)。 \(Q\) 次单点修改(\(a_{p}=v\))且相互独立,
要求输出在每次修改后整个 \(a\)
数组好的子数组的数目。
\(a_{i},n,Q \leq 2e5\)
思路:
C1 没有修改, 仅询问一次, 我就固定遍历左端点, 二分能达到的右端点,
提前递推一个辅助数组判断 \(i\)
端点开头的线段在哪儿结束即可, 网上更简单的做法是 DP 或直接双指针弄一下。
带修之后双指针不行了, 但还可以用来处理初始答案,
我们注意到每次更新会改变一段连续端点开头的线段,
因为它们的右端点一定是递增的。
设 \(i\) 端点开头的线段结束点为 \(j\) , 这里定义为线段右端点后面的一个点,
单点更新可能会造成结束点的点值增加, 增长线段长度,
我们还要处理若结束点增长到足够大时以 \(i\)
节点为开头的新的线段长度(或新的线段长度与原线段长度的差分),
至于结束点是否真的能增长到足够大我们在统计时再判断好了,
从前往后的起始节点若拥有同一个结束点,
那么它们对结束点的要求一定是越来越低的, 若已知 \(p,v\) , 这部分的约束为 \(max(1,p-v+1)\) , 再与其他的约束取个 \(max\) 即可,
这里求的是增加点值可能影响的线段区间的左端点最小值。
谈远了……要维护新的线段长度我们可以直接上线段树二分, 之前优先处理 \(a_{i}-i\) 较大的位置, 线段树二分出结束点
\(j\) , 更新 \(j\) 点, 求出新的终点(新长度与原长度的差分),
再把 \(j\) 点更新回来。对结束点,
长度查分大小都做要一个前缀和。长度查分大小的前缀和可以帮我们统计在 \(v>a_{p}\) 时 \(p\) 点的增长对左边造成的影响。
至于 \(v<a_{p}\) 的情况,
它会对左边以 \(\geq p+1\)
为结束点的线段产生影响, 最多能影响到 \(max(0,p-v)\) 位置,
同样求出区间后我们拿结束点前缀和搞一搞就能统计了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60bool cmp(int a, int b) {return ar[a]-a>ar[b]-b;}
void upd(int n, int s, int e, int pos, int val){
if(s==e&&s==pos) {t[n]=val; return;}
else{
int mid=(s+e)>>1, ln=2*n, rn=2*n+1;
if(pos<=mid) upd(ln,s,mid,pos,val);
else upd(rn,mid+1,e,pos,val);
t[n]=min(t[ln],t[rn]);
}
}
int find(int n, int s, int e, int L, int R, int val){
if(s>R||e<L) return N+1;
else if(s>=L&&e<=R) {
if(t[n]>val) return N+1;
if(s==e) return s;
}
int mid=(s+e)>>1, ln=2*n, rn=2*n+1;
if(t[ln]<=val) return find(ln,s,mid,L,R,val);
else return find(rn,mid+1,e,L,R,val);
}
signed main(){
N=read();
for(int i=1;i<=N;i++) ar[i]=read(), id[i]=i;
sort(id+1,id+1+N,cmp); //high delta (ar[i]-i) first
int ans=0;
for(int i=1,j=0,r=1;i<=N;i++){ //pointer i, pointer r, j is for the addition of ar[id[j]]
while(j+1<=N && ar[id[j+1]]-id[j+1]+i-1>=0) {// Solved by delta order, so we can put two pointers on it instead of restart every time
j++; //id[j] represent the things now we can reach.
upd(1,1,N,id[j],1);
}
r=find(1,1,N,i,N,0); // r represent the things nearest we can not reach. ~\Sacred Binary Search/~
R[i]=r; ans+=r-i;
if(r<=N) {
upd(1,1,N,r,1); //remove the obstacle r
nxt[i]=find(1,1,N,i,N,0)-R[i]; // if we remove the obstacle r, the extra distance we can extend is nxt[i].
upd(1,1,N,r,0); //regain the obstacle r
}
}
for(int i=1;i<=N;i++) prenxt[i]=prenxt[i-1]+nxt[i]; //prefix of nxt[]
for(int i=1;i<=N;i++) preR[i]=preR[i-1]+R[i]; //prefix of R[]
Q=read();
while(Q--){
int pos=read(), val=read();
if(ar[pos]==val) cout << ans << '\n';
else if(ar[pos]<val){ //we will get higher score
int RB=upper_bound(R+1,R+pos,pos)-R-1; // R+1 first - 1 = R last
int LB=lower_bound(R+1,R+pos,pos)-R; //R first
LB=max(LB,max(ll(1),pos-val+1)); // only increasing enough value can let others getover the obstacle.
if(LB>RB) cout << ans << '\n';
else cout << ans+prenxt[RB]-prenxt[LB-1] << '\n';
}
else if(ar[pos]>val){ //we will get smaller score
int LB=upper_bound(R+1,R+pos,pos)-R; //R+1 first = first affected
int RB=max(ll(0),pos-val); // last affected
if(LB>RB) cout << ans << '\n';
else cout << ans-(preR[RB]-preR[LB-1])+(RB-LB+1)*pos << '\n'; // mind the non-answer part adding and erasing
}
}
return (0-0);
}
E
Editorial 都拖着不出, 不想补……
Codeforces Global Round 23 22/10/15
\((1711\rightarrow1712,
rk1691)\)
被 D 诈骗力, 应该三十分钟离场去打游戏的, 看起来这场都是妙妙题, 我不会做,
但我大受震撼。
D
题意:
给定一颗 \(1\) 为根节点的 \(n(n \leq 2e5)\) 个节点树,
每个节点有一个权值 \(s_{i}(s_{i} \leq
1e4)\) , 一个 \(k(k \leq 1e9)\)
条简单路径的多重集称为合法,
当且仅当满足下面的条件:
- 每条路径从根节点开始 - 设 \(c_{i}\)
为经过 \(i\) 节点的路径数, 若 \(u, v\) 拥有共同的祖先, 则 \(|c_{u}-c_{v}| \leq 1\)
给定 \(k\) , 问 \(\sum c_{i}* s_{i}\) 的最大值。
思路:
显然能注意到的一点是, 为了让答案更大, 所有的路径都要延伸到叶节点, 即 $
{v son{u}}{c_{v}}= c_{u}$ 。
设节点 \(u\) 有 \(x\) 个儿子, 所以 \(\forall v \in son_{u}, \; c_{v}= \lceil c_{u}/x
\rceil \;or\; \lfloor c_{u}/x \rfloor\) ,
我们可以将这两种状态设为 \(f_{v,1}\) 和
\(f_{v,0}\) , 我们求出 \(u\) 的每个儿子的两种状态, 让 \(c_{u} \; mod \; x\) 个取 \(1\) 状态, 剩下的取 \(0\) 状态, 这个可以通过排序解决, 具体来说,
我们按 \(f_{v,1}-f_{v,0}\) 排序,
增量越大越优先。总的思想是树形DP, 这个很好想, 但我不会实现……
代码:link
我们默认 \(\lceil c_{u}/x \rceil = \lfloor
c_{u}/x \rfloor + 1\) , 至于是不是其实无所谓……
E1
又到了奇妙的交互+构造题
题意:
给定一个 \(n(n \leq 1e5)\) ,
让你猜一个数 \(x \in [1,n]\) , 至多
\(82\) 次猜测,
每次你可以询问 \([1,n]\) 中的一个子集, 回复你 \(x\) 在不在这个子集中, 但是系统可能说谎,
不过可以保证连续的两次询问中一定有一次系统没有说谎,
\(x\)
的值可能随着询问而动态改变, 不过一定满足之前的约束。
你一共有两次猜测 \(x\)
的机会。
思路:
这个 \(82\) 实在是看不出什么名堂,
思考一下我们怎么保证得到正确且有用的信息, 来缩小范围。
我们可以将数字集合分为不相交的 \(A, B, C,
D\) 四部分, 询问 \(A \cup B\)
以及 \(C\) , 设 \(True\) 为回复在这个子集里, \(False\) 为回复不在这个子集里,
我们可以分类讨论:
1. \(A \cup B=True, \; C=False\)
1.1 前者说谎且后者未说谎, 实际为 \(A \cup
B=False, \; C=False\) , 可排除 \(A, B,
C\) 。
1.2 前者未说谎且后者未说谎, 实际为 \(A \cup
B=True, \; C=False\) , 可排除 \(C,
D\) 。 2. \(A \cup B=True, \;
C=True\)
2.1 前者说谎且后者未说谎, 实际为 \(A \cup
B=False, \; C=True\) , 可排除 \(A, B,
D\) 。
2.2 前者未说谎且后者说谎, 实际为 \(A \cup
B=True, \; C=False\) , 可排除 \(C,
D\) 。 3. \(A \cup B=False\)
等价于 \(C \cup D=True\) 进行 \(swap(A \cup B), swap(C \cup D)\) 即可。
上述的分类讨论都省去了矛盾的部分, 我们固定了 \(A \cup B\) , 加入了更多的约束,
现在我们可以根据 \(C\) 的 \(True/False\) 来排除部分数集, 取一下交集,
我们可以在 \(C=False\) 时排除 \(C\) 部分, 在 \(C=True\) 时排除 \(D\) 部分。
这样每两次操作我们可以把数据规模大小从 \(n\) 变为 \(\lceil
\frac{3}{4}* n \rceil\) 。
如果还剩余三个及以下的数怎么办? 因为最后可以问两次,
我们只要考虑剩三个数时的策略即可。
设这三个数为 \(A, B, C\) , 询问 \(A, B\) 各一次, 则:
1. \(A=True, \; B=True\) 因为 \(A, B\) 不可能全为假, 则 \(C\) 一定为假, 可以排除 \(C\) 。 2. \(A=True, \; B=False\) 分类取交集可排除 \(B\) , 具体见下。
2.1 前者说谎且后者未说谎, 实际为 \(A=False,
B=False\) , 可排除 \(A,
B\)
2.2 前者未说谎且后者说谎, 实际为 \(A=True,
B=True\) , 矛盾
2.3 前者未说谎且后者未说谎, 实际为 \(A=True,
B=False\) , 可排除 \(B, C\) 3.
\(A=False, \; B=True\) 分类取交集可排除
\(A\) , 与 2. 同理。
4. \(A=False, \; B=False\) ,
我们可以再问一次 \(B\) , 然后再问一次
\(A\) 决定排除谁, 具体见下。
4.1 重问中存在 \(True\) 的回答,
一定可以转化为上面三种大状况之一。
4.2 重问也全为 \(False\) , 因为两次的
\(B\) 是连续询问的且全为 \(False\) , 所以我们可以排除 \(B\)
艹!好难想!
代码: link
Educational Codeforces Round 137 (#Div2) 22/10/17
\((1712\rightarrow1791,
rk377)\)
好! DP 不会! 但糊了D! 希望下次继续!
E
题意:
有一个敌人, 血量为 \(h\) ,
你有两把武器, 伤害和攻击冷却时间分别为 \(p_{1}, t_{1}, p_{2}, t_{2}\)
。当武器冷却完成时, 你可以使用一把,
或是等到两把武器都冷却完成时一起使用, 会造成 \(P-s\) 的伤害, 其中 \(s\) 是一个给定的值(护盾?), \(P\) 是使用的武器的伤害的总和。
问可以消灭敌人(使其血量 \(\leq
0\))的最少时间(初始两把武器都需要完全冷却)。
\(1 \leq h,p_{1},p_{2} \leq 5000, 1 \leq s
< min(p_{1},p_{2}), t_{1}, t_{2} \leq 1e12\)
思路:
\(\tt{dp}\) 是显然的,
状态是不会列的。
考虑到每次同时使用两把武器时, 冷却时间都重置为 \(0\) , 转化为一个更低 \(h\) 的子问题。
我们直接设 \(f[i]\) 表示造成 \(i\) 点伤害所需的最短时间, \(f[i]\)
可以通过单发射击以及更复杂的齐射转移而来。
\[f[i]=min(f[max(0,i-(p_{1}-s))]+t_{1},f[max(0,i-(p_{2}-s))]+t_{2})\]
这代表造成 \(i\)
点伤害的最短时间可以由造成 \(i-p_{1}\)
或 \(i-p_{2}\) 伤害的最短时间加上 \(t_{1}\) 或 \(t_{2}\) 的冷却时间转移。
接下来考虑复杂转移:考虑进行 \(j\)
次射击某一把武器, 其中最后一次是齐射, 下文以 \(j\) 次使用第一把武器射击为例:
第一把的独立贡献为: \((j-1)*
(p_{1}-s)\)
第二把的独立贡献为: \((j* t_{1}-t_{2})/t_{2}*
(p_{2}-s)\)
齐射的贡献为: \(p_{1}+p_{2}-s\)
总贡献为:
\[D=(j-1)* (p_{1}-s)+(j* t_{1}-t_{2})/t_{2}*
(p_{2}-s)+p_{1}+p_{2}-s\]
转移方程为: \(f[i]=min(f[i],f[max(0,i-D)]+j*
t_{1}\)
使用另一把武器同理, 总复杂度为 \(O(n^2)\)
代码:link
F
矩阵 + 线段树, 不会矩阵……
G
DP
Educational Codeforces Round 138 (#Div2) 22/10/20
\((1791\rightarrow1780,
rk1050)\)
后排膜 \(\color{black}{\tt{L}}\color{red}{\tt{STM\_\_}}\)
三十场题解了, 还是只会ABC, 怎么办呢?
在家的效率很差, 很有发癫的冲动, 或是进行强迫性摆烂行为。
唯一的梦想是 codeforces 上 1900, 可能还有一个出codeforces div2的梦想,
但那个不着急。写不出来什么了, 我高中以来没有什么表达的冲动,
憋这几行字就是极限了, 有点伤心。
D
题意:
对于一个数组 \(a\) , 如果 \(gcd(a_{i},i)=1\) 就可以删除第 \(i\)
个元素并把后面的元素前移并重新标号。
现在给定 \(n, m(n \leq 3e5, m \leq
1e12)\) ,
要求求满足以下条件的有多种删空数组的方式的数组的数目:
- \(a\) 的长度小于 \(n\) - \(a_{i}
\leq m\)
思路:
正难则反, 考虑仅有一种删空方式的数组的删除序列, 一定是 \(1,1,1,...\) 形式的。这要求第一个数随便取,
第 \(i\) 个数必须与 \([2,i]\) 内的每个数不互质,
所以我们把 \([2,i]\)
内的每个质数乘起来就好了。
代码:link
E
题意:
给定 \(n * m(n* m \leq 4e5)\) 的棋盘,
初始存在一些仙人掌, 你要再种最少数量的仙人掌使得没有第一行到第 \(n\) 行的路径,
种仙人掌的格子之间不能有公共边。
思路:
仙人掌分割第一行与第 \(n\)
行等价于存在一条第一列到第 \(m\)
列的仙人掌路径, 于是去写一个 bfs, 于是过了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67int N, M, T;
int dx[5]={1,1,1,-1,-1}; //注意 dx[0]/dy[0] 的不同
int dy[5]={1,1,-1,-1,1};
int dx2[5]={0,1,0,-1,0};
int dy2[5]={0,0,-1,0,1};
struct node {int x, y;};
int main(){
// freopen("testdata.in","r",stdin);
T=read();
while(T--){
N=read(); M=read();
vector<vector<int>> mp(N+2, vector<int>(M+1)), dis(N+1, vector<int>(M+1, inf)), pre(N+1, vector<int>(M+1));
for(int i=1;i<=N;i++){
string s;
cin >> s; s=" "+s;
for(int j=1;j<=M;j++)
mp[i][j]=(s[j]=='#');
}
deque<node> q; //depue push_front, pusk_back 控制访问顺序, 因为我不会 lambda
for(int i=1;i<=N;i++){
if(mp[i][1]==1){
dis[i][1]=0; pre[i][1]=0;
q.push_front((node){i,1});
}
else if(mp[i][1]==0&&mp[i-1][1]+mp[i+1][1]<1){ //不是所有第一列的点都能作为初始点
dis[i][1]=1; pre[i][1]=0;
q.push_back((node){i,1});
}
}
while(!q.empty()){
node tmp=q.front(); q.pop_front();
int x=tmp.x, y=tmp.y;
for(int i=1;i<=4;i++){
int nx=x+dx[i], ny=y+dy[i];
int tag=0;
for(int j=1;j<=4;j++) { //判断 bfs 到的点能否种植仙人掌, 不写成函数因为我不会 lambda
int nnx=nx+dx2[j], nny=ny+dy2[j];
if(nny>M||nny<1||nnx>N||nnx<1) continue;
if(mp[nnx][nny]) tag=1;
}
if(nx<1||ny<1||nx>N||ny>M||dis[nx][ny]!=inf||tag) continue;
pre[nx][ny]=i; //保存转移路径, 最后回溯
dis[nx][ny]=dis[x][y];
if(mp[nx][ny]==1) q.push_front((node){nx,ny});
else dis[nx][ny]++, q.push_back((node){nx,ny});
}
}
int ans=inf, pos=-1;
for(int i=1;i<=N;i++){
if(dis[i][M]>=ans) continue;
ans=dis[i][M], pos=i;
}
if(pos==-1) {cout << "NO\n"; continue;}
int tmpM=M;
while(tmpM) { //回溯, 第一列用 dx[0]/dy[0], 有点丑
int x=dx[pre[pos][tmpM]], y=dy[pre[pos][tmpM]];
mp[pos][tmpM]=1;
pos-=x; tmpM-=y;
}
cout << "YES\n";
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++)
mp[i][j]?cout << "#":cout << "."; cout << '\n';
}
}
return (0-0);
}
F
于 22.11.21 晚尝试补题, 拖了一个月, 看看之前发癫的人。
题意:
给定一颗树, 点有点权, 初始为 \(0\) ,
有以下两种操作:
1.询问某点点权
2.将树上所有到 从 \(u\) 到 \(v\) 的路径的距离不超过 \(d\) 的点的点权加上 \(k\)
\(n, q \leq 2e5, d \leq 20, k \leq
1000\)
思路:
\(d=0\) 就是经典的树链剖分问题了, \(d \neq 0\) 怎么办, 看到 \(d\) 的范围很小, 考虑暴力维护, 。
具体怎么维护呢?我们可以先简化问题, 每次只更新一个点 \(u\) 。我们可以设 \(bit[u][d]\) 记录对于每个点 \(u\) , 在 \(u\) 的子树中距离 \(u\) 的距离为 \(d\)
的节点增加的权值。这么定义是因为这些节点只有 \(u\) 才能 "够到" 。每次我们更新一个 \(u\) 点, 我们要更新 \(bit[u][d]\) , \(bit[fa[u]][d] \;\&\&\;
bit[fa[u]][d-1]\) , \(bit[fa[fa[u]]][d-1] \;\&\&\;
bit[fa[fa[u]]][d-2].....\) 直到 \(d=0\) 为止, 做到不重不漏。
每次更新一条链也是同理的, 我们把链总可以拆成自顶向下的一段或两段,
设这样的一段链 u-v 中, \(dep[u] \leq
dep[v]\) , 对于 \([u+1,v]\)
这些节点, 我们更新 \(bit[i][d]\) ,
而对于 \(u\) 及以上的点, 我们更新 \(bit[fa[u]][d] \;\&\&\;
bit[fa[u]][d-1]\) , \(bit[fa[fa[u]]][d-1] \;\&\&\;
bit[fa[fa[u]]][d-2].....\) 这样同理向上, 跳一格, 更新两格。
在询问一点 \(u\) 的权值时, 我们只要把
\(bit[u][0], bit[fa[u]][1], ...,
bit[n][d]\) 求和就行了, 复杂度 \(O(20 *
n log^2 n)\)。 代码: link
注意若暴力上跳时, 若 \(d\) 还没有
"用完" , 但已经跳到根节点了, 就要在根节点把 \(d\) 用完。
Codeforces Round 829 (#Div2) 22/10/23
\((1779\rightarrow1816,
rk400)\)
这是 10/23 打的第一场比赛, 难度偏低, 第一次糊出五题(如果C1,
C2算两题的话……)。 E 简单期望不会…… 其中 C2 和 D 都是糊一个结论过的……
上了 \(1800\), 但只上了 2h……
E
题意:
给定一个长度为 \(n\) 的 \(01\) 数组 \(a\) , 每次随机选择两个数, 若 \(i>j \;\&\&\; a_{i}<a_{j}\)
则交换, 期望多少次能让数组变得有序(升序)。
思路:
不会期望, 直接被吓跑力~
假设 \(a\) 中有 \(cnt_{0}\) 个 \(0\) , 那么它们一定在前 \(cnt_{0}\) 个位置,
我们的有效操作就是把前 \(cnt_{0}\) 个数中的 \(1\) 与后面的 \(0\) 交换, 设前 \(cnt_{0}\) 个数中有 \(x\) 个 \(1\) , 则后面也一定有 \(x\) 个 \(0\) , 所以有效操作的概率为 \(\dfrac{x^2}{C_n^2}\) , 期望为概率的倒数, 即
\(\dfrac{C_n^2}{x^2}\) ,
每一步加上就是最后的答案。
代码:link
F
题意:
在 \(n \times m (n \times m \leq
3e5)\) 的沙滩方格上有一些 \(1 \times
2\) 的躺椅, \(1 \times 1\)
的障碍和一些空格, 你想要找到 \(1 \times
2\) 的空地放下自己的躺椅。障碍不可移动, 你可以花费 \(p\) 使得一个躺椅旋转 \(90\) 度放置, 也可以花费 \(q\) 使得一个躺椅沿着长边方向平移一格,
移动躺椅需要保证移动后的位置是没有障碍的。问找到 \(1 \times 2\) 空地的最小移动花费,
或报告无法找到空地。
思路:
从 \(1 \times 2\)
的躺椅联想到黑白染色, 若将躺椅的移动看成空格的移动,
不难发现每次都是黑格移到黑格, 白格移到白格,
最后我们放置躺椅的位置也是一黑一白的。
我们可以证明, 在最佳情况下, 每个躺椅的移动不超过一次,
我有一个感性的理解, 每次移动要么从黑格移到黑格, 要么从白格移到白格,
若移动两次说明既进行了一次黑格的移动也进行了一次白格的移动,
然而考虑躺椅及其周围一共八个格子,
分类讨论发现这两次移动总可以被一次更好的移动直接替代来获取 \(1 \times 2\) 的空地……
我们从所有的空地出发, 对于所有的躺椅,
从躺椅四周的点往躺椅的一端连一条带权有向边表示空地的移动,
跑一遍 \(dijkstra\) ,
最后找一下相邻两格的权值和最小值就做完了……
代码:link
若把图黑白染色, 也可以把本题看成将图的最大匹配 \(+1\) 所需的最小权值, 看题解评论有人说这个,
不知道能不能做。
Codeforces Round 830 (#Div2) 22/10/23
\((1816\rightarrow1769,
rk1321)\)
这是 10/23 打的第二场比赛, 难度偏高, C1 > D1。糊了个D1, 但 C1, C2
不会, C1 寄了五发, 把上一场加的分全打回去了, 还倒欠 \(10\) 分, 警钟敲烂!
C1&C2
题意:
给你长度为 \(n\) 的数组 \(a\) , \(Q\) 次询问给出 \(L_{i}, R_{i}\) , 让你找出一个子数组 \(a[l,r]\) , 满足 \(L_{i} \leq l \leq r \leq R_{i}\) 且 \(f(l,r)=sum(l,r)-xor(l,r)\) 最大,
有多个最大值时要求 \(r-l+1\) 最小,
对于每个询问输出 \(l,r\)。
其中 \(sum(l,r)=\sum\limits_{i=l}^{r}{a_{i}}\) ,
\(xor(l,r)=a_{l} \oplus a_{l+1} \oplus ...
\oplus a_{r}\) 。
\(n \leq 1e5, a_{i} \leq 1e9\) ,
简单版本 \(Q=1\) , 困难版本 \(Q=n\) , 钦定 \(L_{1}=1, R_{1}=n\)
思路:
\(Q=1\)
的情况糊了个二分但是一直错……
注意到做区间最小 \(xor\) 本来是要上
\(trie\) 的, 但是考虑每加一个数 \(x\) 时, \(xor\) 的变化一定小于等于 \(sum\) 的增量, 所以有 \(f(l,r) \leq f(l,r+1)\) ,
数组长度越长答案越优, 最大值肯定要选取整个数组,
接下来我们二分长度找到最短长度使得最大值不下降即可。
\(Q=n\)
的情况就要利用到一些性质了……
首先, \(0\) 蛋用没有, 没有任何贡献,
还占长度, 答案去掉前导 \(0\) 或后缀
\(0\) 一定更优。
假设现在我们选取给定的 \([L_{i},R_{i}]\) 整个子数组,
现在我们考虑什么情况下 \(f(L_{i},R_{i})\) 会减少, 删去一个数, 若
\(xor\) 的减量小于 \(sum\) 的减量时更劣,
因此每个二进制位只能被删除操作覆盖最多一次,
否则第二次覆盖时 \(xor\) 的减量更小(0
-> 1, 或是第一次时就不能覆盖, 0 -> 1), 因为 \(10^9 < 2^{30}\) , 我们只考虑 \([L_{i},R_{i}]\) 内前 \(31\) 个非零数和后 \(31\) 个非 \(0\) 数中选出左右端点即可, 若非 \(0\) 数凑不齐 \(31\) 个……直接双重循环暴力吧……注意特判 \([L_{i},R_{i}]\) 全为 \(0\) 的情况。
具体实现上, 需要再处理一个非 \(0\)
数字数目的前缀和, 以及每个数前面/后面的第一个非 \(0\) 数字。
代码:C1,
C2
事实上, C1 代码太丑了, 直接看 C2 就行。
D2
题意:
一开始给你一个集合, 只包含 \(0\) ,
接下来有 \(Q \leq 2e5\) 次操作,
每次操作可能是下列形式的一种 - 往集合中添加 \(x\) - 在集合中删除 \(x\) (保证 \(x\) 已在集合中) - 查询集合的最小未出现过的
\(x\) 的倍数(x-mex)
D1 没有删除操作, 你直接记忆化暴力, 用一个 \(last[k]\) 存储上一次询问 k-mex 的答案,
下次再询问到时从那儿再更新就行了, 有删除操作时我们也可以仿照 D1。
具体地, 我们开一个 map<int,set
代码:link
有点抽象……
Codeforces Round #831 (Div. 1 + Div. 2) 22/10/29
\((1769\rightarrow1819,
rk712)\)
第一次场上做出 E, 泪目, 虽然这个 E 只有 1800……
F
题意:
给你一个含有 \(n \leq 2000\)
个整数的数组 \(a(1 \leq a_{i} \leq n)\)
, 对于每个 \(a_{i}\) 添加一个元素集
\(\{a_{i}\}\)
定义一次操作由以下两步构成:
- 选择两个集合 \(S, T\) , 满足 \(S \cap T = \emptyset\) - 删除集合 \(S, T\) , 添加集合 \(S \cup T\)
在进行 \(0\) 次或多次操作后,
我们构造一个可重集合 \(M\) 表示当前剩下的所有集合的大小。举个例子,
若当前剩下的集合为 \(\{5\}, \{8\},
\{2,5,12,4\}\) , 则 \(M\) 为
\(\{1,1,4\}\) 。现在让你求出所有不同的
\(M\) 的数量, 对 \(998244353\) 取模。
思路:
让我们层层推进。
1、所有的 \(M\) 集合都可以通过在后面补
\(0\) 变成大小为 \(n\) 的集合, 记 \(M\) 集合中的元素为 \(m_{1}, m_{2}, m_{3}, ..., m_{n}\) ,
让我们以 \(m_{1} \geq m_{2} \geq m_3 \geq ...
\geq m_{n} \geq 0\) 为 \(M\)
中的元素排序, 直觉告诉我们, 一个 "更大" 的合法集合如 \(M=\{11,3,2,1,0,0...\}\) 可以直接拆成 "更小"
的合法集合, 如 \(M'=\{6,5,3,2,1,0,0...\}\)
2、现在定义何为 "更大" , 令 \(M\)
为原集合的前缀和集合, \(\{11,3,2,1,0,0...\}
\Rightarrow \{11,14,16,17,17,17...\}\) 。 对于两个集合 \(M, M'\) , 若 \(\forall\;i \in [1,n], m_{i} \geq
m'_{i}\) 则 \(M\)
更大。
3、记 \(cnt_{i}\) 为 \(a\) 数组中数字 \(i\) 出现的次数, 可以看出来, "最大"
的集合只有一个, 我们把出现过一次及以上的数的个数记为 \(m_{1}\) , 出现过两次及以上的数的个数记为
\(m_{2}\) …… 这样我们可以定义出 \(M\) , 若按照刚刚的前缀和的定义,
\[m_{i}=
\sum\limits_{j=1}^{n}{min(cnt_{j},i)}\]
(注意上文的 \(j\) 不是
\(a_{j}\))
现在回到原始定义, 那么一个合法的 \(M\)
集合就要满足:
\[\forall k \in [1,n],
\sum\limits_{i=1}^{k}{m_{i}} \leq \sum\limits_{j=1}^{n}{min(cnt_{j},k)}
\;\;and\;\; \sum\limits_{i=1}^{n}{m_{i}}=n\]
我们考虑进行 DP 。
4、设 \(lim[i]=\sum\limits_{j=1}^{n}{min(cnt_{j},i)}\)
, 我们考虑一个三维的 \(f[p][sum][las]\)
表示 \(M\) 已经填了 \(p\) 位, \(p\) 位的和为 \(sum\) , 第 \(p\) 位(最后一位)为 \(las\) 时的方案数, 则有如下转移:
\[f[p][sum][las]=\sum f[p-1][sum-x][x], x
\geq las, sum \leq lim[p]\]
\(x \geq las\) 是因为 \(m_{1}, m_{2}, ..., m_{n}\) 单调不降,
转移后再令:
\[f[p][sum][las]=\sum\limits_{i=las}^{n}{f[p][sum][i]}\]
做后缀和可以把 \(O(n^4)\) 的复杂度降到
\(O(n^3)\) ,
空间复杂度可以通过滚动数组降到 \(O(n^2)\) , 然而 \(O(n^3)\)
的时间复杂度还是无法通过本题。
5、考虑 \(las\) 作为最后一个数, 有
\(n \geq p *las\) , 所以 \(las \leq n/p\) , 总的复杂度为调和级数形式,
\(O(n*n \; \log \; n)=O(n^2\;log\;n)\)
。
代码:link
因为本题的转移在前缀和优化后其实就是一个 \(O(1)\) 的赋值,
我的滚动数组会出现奇奇怪怪的错误, 就直接开两个数组 \(f, g\) 了, 同时后缀和的开头要大一点,
要让后面的完全覆盖前面的值, 同时注意 \(g\) 数组的初始化……
Codeforces Round 832 (#Div2) 22/11/4
\((1819\rightarrow1792,
rk1231)\)
进行一个烂的摆, D不会, A, B各吃一发罚时, 寄。
D
题意:
长度为 \(n\) 的数组 \(a\) , \(Q\) 次独立询问, 每次询问给出一个 \([L_{i},R_{i}]\) 区间,
你可以在区间内进行任意次操作:
-选择 \(l, r (L_{i} \leq l \leq r \leq
R_{i})\) 且 \(r-l+1\)
为奇数
-将 \(a_{l}, a_{l+1}, ..., a_{r}\)
赋值为 \(a_{l} \oplus a_{l+1} \oplus ...
\oplus a_{r}\)
问能将 \(a[L_{i},R_{i}]\) 区间整体置
\(0\) 的最小操作次数, 或输出 \(-1\) 表示不可能。
\(n, Q \leq 2e5, 1 \leq a_{i} \leq
2^{30}\)
思路:
寄!就差最后一步……
若区间异或和不为 \(0\) , 直接输出 \(-1\) 。
若区间全为 \(0\) , 直接输出 \(0\) 。
若区间长度为奇数, 我们可以直接操作整个区间, 输出 \(1\) 。
若 \(a[L_{i}]=0\) 或 \(a[R_{i}]=0\) , 我们可以忽略这一个长度,
然后输出 \(-1\) 同上。
重点 , 若以 \(a[R_{i}]\) 为右端点, 存在某一段区间异或和为
\(0\) 且这段区间的左端点 \(lb \geq L_{i}\) 且 \(lb\) 与 \(R_{i}\) 奇偶性相同, 输出 \(2\) 。
否则剩余情况输出 \(-1\) 。
若答案 \(\geq 3\) ,
中间的区间一定能被并入两边区间, 你可以手玩一下,
若中间的并入两边的某一个区间后新的区间长度为奇数就正好,
若并上两边的区间长度都为偶数我们就直接三个区间并在一起。
我们维护以一个点为右端点的最小的异或和为 \(0\) 的区间, 只要开一个 二维 \(map\) , 第一维大小为 2,
来回跳就可以了。
代码:link
E
2900 的 E, 补你**
CodeTON Round 3 (Div.1+Div.2) 22/11/6
\((1792\rightarrow1732,
rk2536)\)
思维僵化, 手速慢, 吃罚时, C写了三遍……, D 看错一个范围(\(a_{i} \leq m \Rightarrow a_{i} \leq n\)),
进行一个分数回调, 从来不开窍, 我癫都懒得发了。
E
题意:
给你一个长度为 \(n(n \leq 2e5)\)
的括号序列, 问你将它的所有(\(n*(n+1)/2\))
的子串变为合法括号序列的最少操作数之和。你有两种操作可用,
分别是选择子串循环右移一格以及插入一个任意括号。
思路:
经典括号匹配问题, 对于一个合法括号序列, 记 \((\) 为 \(+1\), \()\) 为 \(-1\) , 它的前缀和不能掉到 \(0\) 以下且总和为 \(0\)。
首先, 因为总和必须为 \(0\) ,
要加的左右括号数是确定的。
然后?然后不会了。
使用 codeforces 题解评论区 \(\color{orange}{\tt{adamant}}\)
的解法:
一个可以手玩出的结论是, 设一个括号序列的最小前缀和为 \(m(m \leq 0)\), 总和为 \(c\) , 需要的最小操作总数为 \(|m|+max(0,c)\)
。可以这么考虑:不管最后哪种括号更多, 中间前缀和小于 \(0\) 的部分都要通过找一个末尾为 \((\) 的子串右移来把前缀和 "拉上来",
右括号更多就可以虚空造左括号来拉前缀和,
左括号更多在拉完前缀和后还要造更多的右括号使得总和为 \(0\)。
我们记这个括号序列为 \(s=(m;c)\) ,
现在考虑分治的思想, 对于括号序列 \(s_{1}=(m_{1};c_{1}), s_{2}=(m_{2};c_{2}),
s_{1}+s_{2}=(min(m_{1},c_{1}+m_{2});c_{1}+c_{2})\) 左边的 \(min\) 表示最小前缀和 \(m\) 要么出现在 \(s_{1}\) 中, 要么出现在 \(s_{2}\) 中。
现在考虑怎么做这个分治, 先把括号序列分为左右两部分(\([0,mid),[mid,n]\)),
算好子串在单个部分内的贡献, 再算子串跨部分的贡献(下文 \(c_{1}, c_{2}\) 等来自 \(s_{1}=[start,mid), s_{2}=[mid,p]\)
两个子串)。
枚举左边的每个括号作为子串的起点, 按照 \(c\) 将右边排序, 找到最远的终点使得 \(c_{1}+c_{2} \leq 0\) , 这样左边的子串的
\(c\) 贡献为 \(0\), 右边的子串的 \(c\) 贡献为 \(c_{1}+c_{2}\)。
枚举左边的每个括号作为子串的起点, 按照 \(m\) 将右边排序, 找到最远的终点使得 \(m_{2} \leq m_{1} - c_{1}\) ,
这样左边的子串的 \(m\) 贡献为 \(|m_{2}+c_{1}|\), 右边的子串的 \(m\) 贡献为 \(|m_{1}|\), 不用担心绝对值符号, 因为取 \(|m_{2}+c_{1}|\) 时, \(m_{2}+c_{1} \leq m_{1} \leq 0\)。
于是应该做完了……
代码:link
虽然有点复杂, 但也是一种做法嘛……
注意代码里前缀后缀满天飞……我尽量注释好了……
复杂度是 \(O(n log^2 n)\) 的吧……
Codeforces Round 832 (#Div2) 22/11/12
\((1731\rightarrow1801,
rk374)\)
最后糊出了D, 好起来了。
E
笛卡尔树, 不会
F
构造, 摆
今天的补题就到这里了, 大家下场再见
Pinely Round 1 (Div. 1 + Div. 2) 22/11/20
\((1801\rightarrow1906,
rk460)\)
上紫了!运气真的很好!
ABC 差不多手速拉满 + 0 dirt
D 在赛时的最后 15 mins 才冲出来, 没有 ABC
的手速和上午刚打的数论小板子我这样的菜鸡估计会寄在 China Round 的 D,
最后贴线上紫。
成功在 NOIP 前最后一场比赛完成退役前上紫的既定目标, 现在别无所求, NOIP
随便打了。
E
题意:
通过 01矩阵 给你一个 \(n \leq 4000\)
节点的无向图, 问你需要至少多少次操作才能让图联通,
每次操作是这样的:
- 任意选择一个 \(u\) 节点 -
对于剩余的所有节点, 如果有 u-v 边, 就断掉, 否则就加上
要求输出最少操作次数和操作序列。
思路:
考虑一下什么时候答案为 \(1\) ,
当场上有孤立点时, 直接操作那个孤立点就行。 我们可以得出一个粗糙的策略,
找到度数最小的点并通过操作与它相邻的所有点把那个点独立,
最后操作那个点。
这个结论对于 E 而言太过简单, 我们想一想反例, 在一个联通块(大小为
siz)中若出现一个度数不为 siz-1 的点, 我们可以直接操作这个点一次,
虽然它的边会断掉, 但它还能连回联通块, 而且也可以连上其他的所有点:
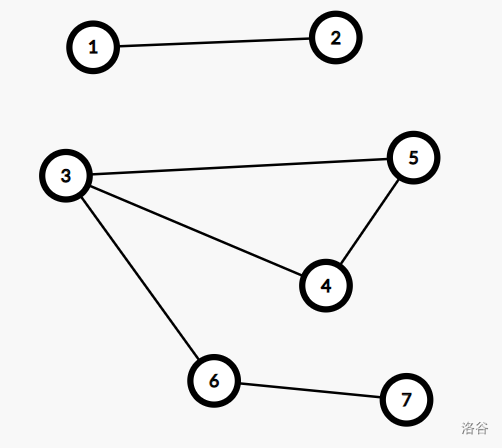
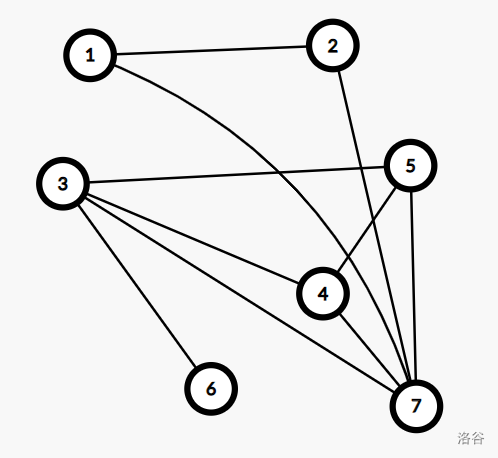
就像这样。 我们还可以发现, 我们不用“死扣一个点”,
如果场上有三个及以上联通块, 我们可以在 1, 3 联通块中任意取一个点出来,
这样保证联通块 2 与其他联通块相联通, 只要两次操作。
当场上只有两个联通块, 内部是完全图(团)的时候,
我们对于节点的操作就相当于把一个节点从一个图拉到了另一个图中, 答案为
min(siz1,siz2)
总结一下零零散散的性质:
图已联通时(联通块数量为 \(1\) )答案为 \(0\)
有孤立点时答案为 \(1\) , 选择那个孤立点
若存在某个联通块内部不是完全图(团)的时候选择其中度数最小的节点, 答案为 \(1\)
若有两个联通块, 答案为 \(min(siz_{1},siz_{2})\) , 输出较小联通块内的所有节点
若有三个及以上联通块, 答案为 \(2\) , 任选两个联通块, 各挑一个点输出。
代码:link
Codeforces exercises 2022